标签:friend 起点 col com names http eof ems 快速
题目传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=4417
我们不难发现,这是一道动归题。
考虑最原始的动归:f[i][j]表示从起点走到(i,j)这个点的方案数。
不难推出f[i][j]=Σ(f[i][j-2k+1]+f[i-1][j-2k+1]+f[i+1][j-2k+1]) 其中k∈[1,floor(j/2)]。floor(x)表示将x向上取整。
显然,这个式子的复杂度为O(n*m^2),愉悦地TLE~。
再研究些许发现其实可以用前缀和优化该式子,复杂度被削掉一个m,变为O(n*m)。但显然,这个还是会超时的,得继续优化。
题目中,n的范围只有50,如果真的是一道单纯的暴力题,n的范围不可能这么小。我们考虑用矩阵快速幂优化该式子。记录答案的矩阵为1*2n的矩阵,该矩阵左侧n个位置存储f[i],右侧n个位置存储f[i-1]。 我们构造一个2n*2n的转移矩阵,转移矩阵需满足记录答案的矩阵乘上转移矩阵后变成左侧n个位置存储f[i+1],右侧n个位置存储f[i]。
大致的样子如图:以n=5的矩阵举例(n为其他的和这个长的差不多),中间十字交叉线是帮助大家理解的,矩阵是10*10的!!
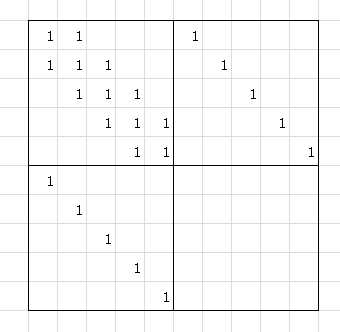
构造矩阵时需特别注意n=1的情况!!(我就被这个坑了)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define M 110 5 #define MOD 30011 6 using namespace std; 7 struct matrix{ 8 int a[M][M],n,m; 9 matrix(){memset(a,0,sizeof(a)); n=m=0;} 10 matrix(int nn,int mm){memset(a,0,sizeof(a)); n=nn; m=mm;} 11 friend matrix operator *(matrix a,matrix b){ 12 matrix c=matrix(a.n,b.m); 13 for(int i=1;i<=a.n;i++) 14 for(int j=1;j<=b.m;j++) 15 for(int k=1;k<=a.m;k++) 16 c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%MOD; 17 return c; 18 } 19 friend matrix operator ^(matrix a,int p){ 20 matrix c=a; p--; 21 if(p<0) {memset(c.a,0,sizeof(c.a)); if(p==-1) c.a[1][1]=1; return c;} 22 while(p){ 23 if(p&1) c=c*a; 24 p>>=1; a=a*a; 25 } 26 return c; 27 } 28 }f,f1,f2,ans1,ans2; 29 int n,m; 30 int main(){ 31 scanf("%d%d",&n,&m); 32 f=matrix(n<<1,n<<1); ans1=ans2=matrix(1,n<<1); 33 ans1.a[1][1]=ans2.a[1][1]=1; 34 for(int i=1;i<=n;i++) f.a[i][i-1]=f.a[i][i]=f.a[i][i+1]=1; 35 f.a[1][0]=f.a[n][n+1]=0; 36 for(int i=1;i<=n;i++) f.a[i][n+i]=f.a[n+i][i]=1; 37 f1=f^(m-1); f2=f^(m-3); 38 ans1=ans1*f1; ans2=ans2*f2; 39 printf("%d\n",(ans1.a[1][n]-ans2.a[1][n]+MOD)%MOD); 40 }
标签:friend 起点 col com names http eof ems 快速
原文地址:http://www.cnblogs.com/xiefengze1/p/7735625.html