标签:open alt mes 输入格式 cst font click pre add
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入格式:
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式:
一行,包含一个正整数,即为该网络的最大流。
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40
50
样例说明:
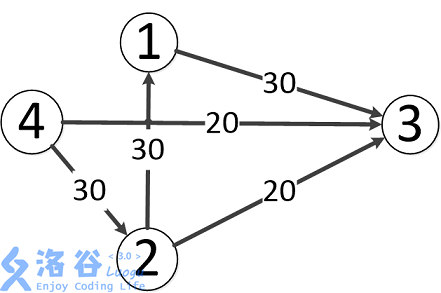
题目中存在3条路径:
4-->2-->3,该路线可通过20的流量
4-->3,可通过20的流量
4-->2-->1-->3,可通过10的流量(边4-->2之前已经耗费了20的流量)
故流量总计20+20+10=50。输出50。
对于100%的数据:N<=10000,M<=100000

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=10010,MAXM=100010; 6 7 struct ABC{int c,to,pre;}e[MAXM*2]; 8 9 int n,m,A,B,C,sz=1,s,t,ans; 10 int las[MAXN],cur[MAXN],gap[MAXN],H[MAXN]; 11 12 void add(int a,int b,int v){ 13 e[++sz].to=b;e[sz].c=v; e[sz].pre=las[a];las[a]=sz; 14 } 15 int ISAP(int x,int F){ 16 if (x==t) return F; 17 int used=0,f1; 18 for (int i=cur[x];i;i=e[i].pre) 19 if (e[i].c>0&&H[e[i].to]+1==H[x]){ 20 f1=ISAP(e[i].to,min(e[i].c,F-used)); 21 e[i].c-=f1;e[i^1].c+=f1;used+=f1; 22 if (e[i].c>0) cur[x]=i; 23 if (F==used) return F; 24 } 25 --gap[H[x]]; 26 if (!gap[H[x]]) H[s]=n+2; 27 ++H[x];++gap[H[x]]; 28 cur[x]=las[x]; 29 return used; 30 } 31 32 33 int main(){ 34 scanf("%d%d%d%d",&n,&m,&s,&t); 35 for (int i=1;i<=m;++i) scanf("%d%d%d",&A,&B,&C),add(A,B,C),add(B,A,0); 36 while (H[s]<n+2) ans+=ISAP(s,1e9); 37 printf("%d",ans); 38 return 0; 39 }
标签:open alt mes 输入格式 cst font click pre add
原文地址:http://www.cnblogs.com/Dance-Of-Faith/p/7738170.html