标签:orm ace 答案 ret 宽度 return cstring bsp 不同
【问题描述】
有一面很长很长的墙。 你需要在这面墙上贴上两行瓷砖。 你的手头有两种不同尺寸的瓷
砖, 你希望用这两种瓷砖各贴一行。瓷砖的长可以用分数表示,贴在第一行的每块瓷砖长度
为A/B贴在第二行的每块瓷砖长度为C/D.
本问题中你并不需要关心瓷砖的宽度。
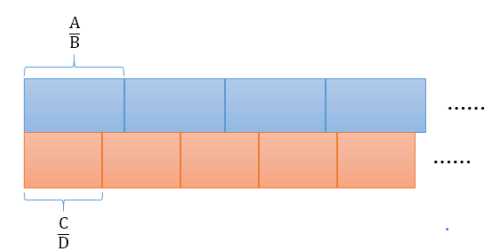
如上图所示, 两排瓷砖从同一起始位置开始向右排列,两排瓷砖的第一块的左端的缝隙
是对齐的。 你想要知道, 最短铺多少距离后, 两排瓷砖的缝隙会再一次对齐。
【输入】
输入的第 1 行包含一个正整数 T,表示测试数据的组数。
接下来 T 行, 每行 4 个正整数 A, B, C, D,表示该组测试数据中,两种瓷砖的长度分别为A/B,C/D.
【输出】
输出包含 T 行, 第 i 行包含一个分数或整数, 表示第 i 组数据的答案。 如果答案为分数,
则以“X/Y”的格式输出,不含引号。分数必须化简为最简形式。如果答案为整数,则输出
一个整数 X。
【输入输出样例 1】
| tile.in | tile.out |
| 2 1 2 1 3 1 2 5 6 |
1 5/2 |
见选手目录下的 tile/tile1.in 与 tile/tile1.out
【输入输出样例 1 说明】
对于第一组数据,第一行瓷砖贴 2 块,第二行贴 3 块,总长度都为 1,即在距离起始位
置长度为 1 的位置两行瓷砖的缝隙会再次对齐。
对于第二组数据, 第一行瓷砖贴 5 块,第二行贴 3 块,总长度都为5/2

分析:实际上就是求最小公倍数.分数的话先通分,然后对分子求最小公倍数就可以了,注意爆int.
#include <map> #include <queue> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; ll T, a, b, c, d; ll gcd(ll a, ll b) { if (!b) return a; return gcd(b, a % b); } int main() { scanf("%lld", &T); while (T--) { scanf("%lld%lld%lld%lld", &a, &b, &c, &d); ll t, t2; t = b / gcd(b, d) * d; a *= (t / b); c *= (t / d); t2 = a / gcd(c, a) * c; if (t2 % t == 0) printf("%lld\n", t2 / t); else { ll p = gcd(t2, t); t /= p; t2 /= p; printf("%lld/%lld\n", t2, t); } } return 0; }
标签:orm ace 答案 ret 宽度 return cstring bsp 不同
原文地址:http://www.cnblogs.com/zbtrs/p/7738330.html