标签:算法 数据结构
首先认识一下什么是“前向星”:
前向星是一个特殊的边集数组,通过将边集数组中的每条边按照起点排序(必要时起点相同的边再按终点排序),并记录下以某个点为起点的所有边在数组中的其实位置和存储长度,来构造前向星。
链式向前星,是图的一种存储结构,采用数组模拟链表实现前向星的功能,简单来讲,它按照边来存图,而邻接矩阵是按照点来存图。
来看一张大牛的PPT:
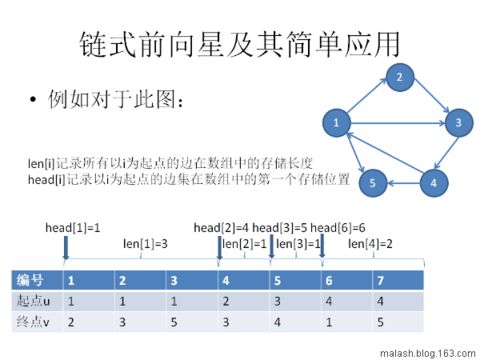
(上面图中有一处错误:head[6]=6,应该改为head[4]=6)
可以看出,利用前向星,我们可以用O(1)的时间找到以i为起点的第一条边,以O(len[i])的时间找到以i为起点的所有边。但是对所有边按起点进行排序,可能会造成更大的时间复杂度,不能有效的优化某些SPFA问题,所以,更加高效的前向星出现了——链式前向星。
根据前向星的定义,构造前向星的主要耗时发生在按照起点或者终点的排序上,即存在频繁的交换。于是将链表引入前向星,就可以不使用排序也可得到同样的效果,这样就产生了链式前向星。
以上图中的图为例:
用head[i]表示以i为起点的第一条边的存储位置,next[i]表示与第i条边同起点的下一条边的存储位置,e[i]表示第i条边的终点。
如果输入顺序为(起点,终点):
①(1,2)
②(2,3)
③(3,4)
④(1,3)
⑤(4,1)
⑥(1,5)
⑦(4,5)
则存储的数据为;
| head[1]=1 | head[2]=2 | head[3]=3 | head[4]=5 | head[5]=0 |
| e[1]=2 | e[2]=3 | e[3]=4 | e[4]=3 | e[5]=1 | e[6]=5 | e[7]=5 |
| next[1]=4 | next[2]=0 | next[3]=0 | next[4]=6 | next[5]=7 | next[6]=0 | next[7]=0 |
设需要找出所有起点为1的边,搜找过程为:
head[1]=1;
e[1]=2,next[1]=4;
e[4]=3,next[4]=6;
e[6]=5,next[6]=0;
结束,输出的边为(1,2),(1,3),(1,5)
即用e[i]输出边,用next[i]寻找下一个以i为起点的边。
链式前向星的具体应用
SPFA,多叉树转二叉树,图的遍历等等
本文出自 “卫莨” 博客,请务必保留此出处http://acevi.blog.51cto.com/13261784/1976538
标签:算法 数据结构
原文地址:http://acevi.blog.51cto.com/13261784/1976538