设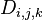 为从
为从 到
到 的只以
的只以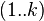 集合中的节点为中间节点的最短路径的长度。
集合中的节点为中间节点的最短路径的长度。
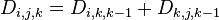 ;
;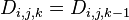 。
。
因此,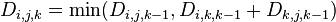 。
。
Floyd-Warshall算法的时间复杂度为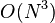 ,空间复杂度为
,空间复杂度为 。
。
Floyd-Warshall算法的描述如下:
for k ← 1 to n do
for i ← 1 to n do
for j ← 1 to n do
if ( ) then
) then
 ←
← 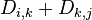 ;
;
其中 表示由点
表示由点 到点
到点 的代价,当
的代价,当 为
∞ 表示两点之间没有任何连接。
为
∞ 表示两点之间没有任何连接。
在实际算法中,为了节约空间,可以直接在原来空间上进行迭代,这样空间可降至二维。
大概的代码为:
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(ans[k-1][i][k]==无穷大||ans[k-1][k][j]==无穷大)
{
ans[k][i][j]=ans[k-1][i][j]; //保持原来的值,即从i到j允许经过前k个点和允许经过前k-1个节点时最短路径长度相同
continue;
}
if(ans[k-1][i][j]==无穷大||ans[k-1][i][k]+ans[k-1][k][j]<ans[k-1][i][j])
{
ans[k][i][j]=ans[k-1][i][k]+ans[k-1][k][j];
}
else
{
ans[k][i][j]=ans[k-1][i][j];
}
}
}
}经过这么多次迭代后,最后a到b的最短路径结果为ans[n][a][b].
与此同时,我们注意到,在通过ans[k-1][i][j]的值来递推求ans[k][i][j]的值时,所有的ans[k][i][j]值将由ans[k-1][i][j]与ans[k-1][i][k]+ans[k-1][k][j]的大小关系来确定,但同时ans[k][i][k]和ans[k][k][j]必定与ans[k-1][i][k]和ans[k-1][k][j]的值是相同的,即这些值不会因为本次更新而发生变化。所以我们将代码简化为:
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(ans[i][k]==无穷大||ans[k][j]==无穷大) continue;
if(ans[i][j]==无穷大||ans[i][k]+ans[k][j]<ans[i][j])
{
ans[i][j]=ans[i][k]+ans[k][j];
}
}
}
} 这样原本空间复杂度O(N3)变为O(N2)了。每次跟新直接在该二位数组上就OK。
原文地址:http://blog.csdn.net/alvine008/article/details/39206657