标签:等价 替换 经典 字典 构造 位置 连通 2-sat 统一
2-SAT:给 $n$ 个布尔变量 $f_1, f_2, ..., f_n$ ,以及一些二元限制条件(例如 $f_x ~ or ~ f_y$),问是否存在解,并求出一组解。
对 2-SAT 问题建图 $G$ 。
点:每个布尔变量 $f_x$ 拆成一个点对 $x, x‘$ ,要求在这个点对中选择一个点。选择了 $x$ 表示 $f_x = 1$ ,选择了 $x‘$ 表示 $f_x = 0$ 。图 $G$ 可以看做一个二分图,将点 $x$ 放在二分图的左部,点 $x‘$ 放在二分图的右部。
边:若 $x \rightarrow y$ ,则点 $x$ 向点 $y$ 连一条有向边。
以 $f_x ~ or ~ f_y = 1$ ,说明连边。
$f_x ~ or ~ f_y = 1 \Leftrightarrow x‘ \rightarrow y, y‘ \rightarrow x$
必要性:如果选择了 $x‘$ ,则 $f_x = 0$ ,由于 $f_x ~ or ~ f_y$ ,所以 $f_y = 1$ ,即选择了 $y$ ,则 $x‘ \rightarrow y$ 。取逆否关系,有 $y‘ \rightarrow x$ 。
充分性:反设 $f_x ~ or ~ f_y = 0$ ,则 $f_x = f_y = 0$ ,这与 $x‘ \rightarrow y$ 以及 $y‘ \rightarrow x$ 都矛盾。
某些狡猾点的 2-SAT 问题,不会把限制条件摆得这么明显,这时候就需要利用命题逻辑的相关知识去转化,这里给出与 2-SAT 问题密切相关的几条公式。
(1) $P \lor (Q \land R) = (P \lor Q) \land (P \lor Q)$
$P$ 成立,或者 $Q, R$ 都成立,等价于 $P$ 或 $Q$ 成立,且 $P$ 或 $R$ 成立。
(2) $\neg (P \lor Q) = \neg P \land \neg Q$
有一个成立都不行,即两个都不成立。
类似地,其他二元限制条件的等价条件也都由某个蕴含关系以及逆否蕴含关系构成,所以图 $G$ 具有左右对称的性质。
假如要给左右对称下一个严格的定义,那就是:若 $x \rightarrow y‘$ ,则 $y‘ \rightarrow x$ 。
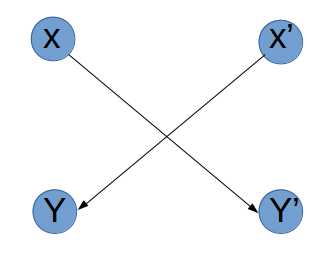
现在的问题被转化为:对图 $G$ 中每个点对选择一个点,若一个点被选择,那么它的所有后继都要被选择,问是否有解,并构造一组解。
选择引理:若某个点 $x \in G$ 如果被选择了,则与它在同一个强连通分量都要被选择。
根据强连通分量的定义,与 $x$ 在同一个强连通分量内的点,都是 $x$ 的后继。
我可以对图 $G$ 通过 Tarjan 算法进行缩点,得到新图 $G‘$ 。
点:将新图中的点按照出栈顺序,从小到大进行标号。由于 $G$ 由若干个点对组成,所以 $G‘$ 也由若干个点对组成,记 $u \in G‘$ 的对应点为 $u‘$ 。对 $x \in G$ ,记 $p_x$ 表示 $x$ 在 $G‘$ 中的对应点。
边:由于图 $G$ 左右对称,所以图 $G‘$ 也满足左右对称。
标号引理:对于 $u, v \in G‘$ ,若 $u \rightarrow v$ ,则 $u > v$ 。
根据新图中点的标号顺序,由于 $u$ 总会在 $v$ 之后出栈,显然有上述命题。
2-SAT 定理:2-SAT 问题有解,当且仅当对于 $x \in [1, n]$ ,$p_x \ne p_{x‘}$ 。
记 $A$ 为 “ 2-SAT 问题有解 ” ,$B$ 为 $x \in [1, n], p_x \ne p_{x‘}$ ,只需要证 $\neg B \Rightarrow \neg A$ ,$A \Rightarrow B$ 。
证 $\neg B \Rightarrow \neg A$ 。当存在 $x$ ,$p_x = p_{x‘}$ 时,若选择了 $x$ ,则必须选择 $x‘$ ,若选择了 $x‘$ ,则必须选择 $x$ ,而 2-SAT 问题要求只能选择 $1$ 个,矛盾。
证 $A \Rightarrow B$ 。根据选择引理,问题可以被看做 $G‘$ 中选点的问题:在 $G‘$ 中的每个点对中选择一个点,且若选择了点 $u$ ,则其所有后继都要被选择。我可以直接构造一组解,对每个点对 $(u, u‘)$ ,选择较小的点。反设有 $u \rightarrow v$ ,选择了 $u$ ,而没有选择 $v$ ,则可以推出矛盾:
$\begin{aligned} u & > v & 标号引理 \\ & > v‘ & 选择方法 \\ & > u‘ & 对称性, 标号引理 \\ & > u & 选择方法 \end{aligned}$
2-SAT 定理除了给出了解的存在性,还给出了一组具体的解:对于 $G‘$ 中的点对 $(u, u‘)$ ,选择 $u$ 和 $u‘$ 中较小的点,即对于 $G$ 中的 $x$ ,选择 $p_x$ 与 $p_{x‘}$ 中较小的点。利用 Tarjan 算法进行标号,所以这个算法的复杂度是线性的,很优秀。
现在将 2-SAT 问题进行拓展,允许存在一元限制条件,例如 $f_x = 1$ 。
$f_x = 1 \Leftrightarrow x‘ \rightarrow x$
必要性:若选择了 $x‘$ ,则强制选择 $x$ ,保证不能作为一组解。
充分性:反设 $f_x = 0$ ,则选择了 $x‘$ ,则选择了 $x$ ,不能作为一组解。
2-SAT 定理是否兼容一元限制条件?
首先,若 $p_x = p_{x‘}$ ,显然无解,否则 $p_x \ne p_{x‘}$ 。
根据实际意义,我要选择 $x$ 。而根据标号引理,$p_{x‘} \rightarrow p_x$ ,所以 $p_{x‘} > p_x$ ,根据 2-SAT 引理的构造方法,会选择 $x$ 。综上,二者得以统一!
[CF 875C] National Property
给定字符集大小 $m(m \le 100000)$ ,每种字符有两种字母:小写字母,大写字母。任意大写字母小于小写字母。
给定 $n(n \le 100000)$ 个总和不超过 $100000$ 的由小写字母组成的单词,问是否存在一种将某些小写字母替换成大写字母的方案,使得这 $n$ 个单词按照字典序排列。
我观察到每种字母有两种选择:不改,改。这像经典的 two-sat 问题。
对于相邻两个字符串 $S$ , $T$ ,注意到相同的前缀不会影响,找到第一个不相同的位置,不妨设靠前的字符串的这个位置是 $x$ ,靠后的是 $y$ 。当 $x$ 不存在时,一定有 $S \le T$ ;当 $x$ 存在,且 $y$ 不存在时,一定有 $S > T$ ,矛盾;当 $x < y$ 时,若选择了 $x$ ,必须选择 $y$ ,若选择了 $y‘$ ,必须选择 $x‘$ ;当 $x > y$ 时,必须选择 $x‘$ 和 $y$ 。
标签:等价 替换 经典 字典 构造 位置 连通 2-sat 统一
原文地址:http://www.cnblogs.com/Sdchr/p/7747057.html