标签:gif res exist jpg print scan nss 矩阵 mos
InputInput a length L (0 <= L <= 10 6) and M.OutputOutput K mod M(1 <= M <= 30) where K is the number of E-queues with length L.Sample Input
3 8
4 7
4 8
Sample Output
6
2
1
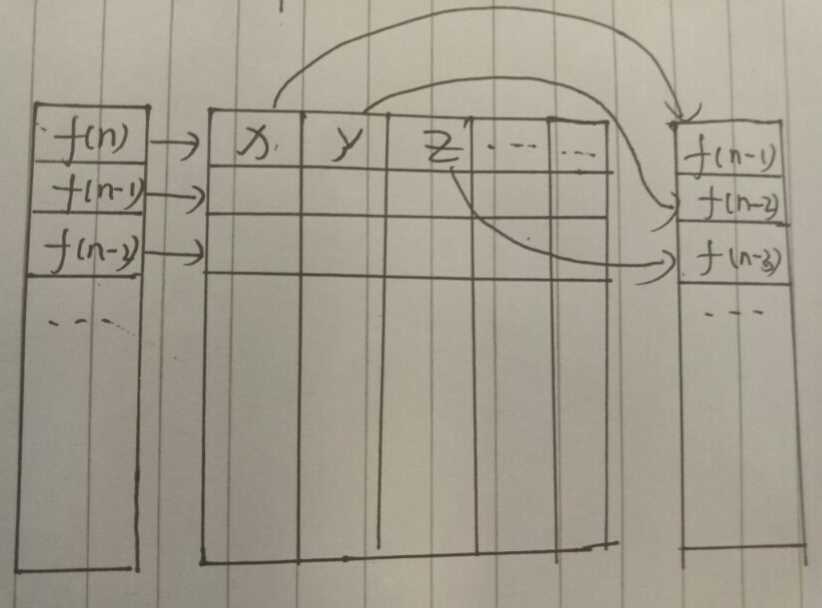
下图是对矩阵的理解,对左边每一个f(n),需要m个f(x)就在第x排记录m。
如图,f(n)=x*f(n-1)+y*f(n-2)+z*f(n-3)...
本题的公式是f(n)=f(n-1)+f(n-3)+f(n-4),分别对最后一位是f或者讨论即可得出。

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<memory>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn=4;
int Mod;
struct mat
{
int m[maxn][maxn],len;
mat(){memset(m,0,sizeof(m));len=maxn;}
mat friend operator * (mat a,mat b){
mat d;
for(int i=0;i<a.len;i++)
for(int j=0;j<a.len;j++){
d.m[i][j]=0;
for(int k=0;k<a.len;k++)
d.m[i][j]+=(a.m[i][k]*b.m[k][j])%Mod;
}
return d;
}
mat friend operator^(mat a,int k) {
mat c;
for(int i=0;i<c.len;i++) c.m[i][i]=1;
while(k){
if(k&1) c=a*c;
a=a*a;
k>>=1;
}
return c;
}
};
int main()
{
int n,k;
mat ans,x,c;
x.m[0][0]=x.m[0][2]=x.m[0][3]=x.m[1][0]=x.m[2][1]=x.m[3][2]=1;
ans.m[0][0]=9;
ans.m[1][0]=6;
ans.m[2][0]=4;
ans.m[3][0]=2;
while(~scanf("%d%d",&n,&Mod)){
if (n<=4){
printf("%d\n",ans.m[4-n][0]%Mod);
}
else {
c=x^(n-4);
c=c*ans;
printf("%d\n",c.m[0][0]%Mod);
}
}
return 0;
}
标签:gif res exist jpg print scan nss 矩阵 mos
原文地址:http://www.cnblogs.com/hua-dong/p/7748357.html