二叉树原理和作用，总结

标签：用途   技术分享   原理   中序   abs   操作   ddb   static   部分   

二叉树

二叉树是一种重要的数据结构，与数组、向量、链表都是一种顺序容器，它们提供了按位置访问数据的手段。但是有一个缺点，它们都是按照位置来确定数据，想要通过值来获取数据，只能通过遍历的方式。而二叉树在很大程度上解决了这个缺点，二叉树是按值来保存元素，也按值来访问元素。

二叉树由一个个节点组成，一个节点最多只能有两个子节点，从根节点开始左右扩散，分左子节点和右子节点，向下一直分支。

许多实际问题抽象出来的数据结构往往是二叉树的形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树是递归定义的。

 

 

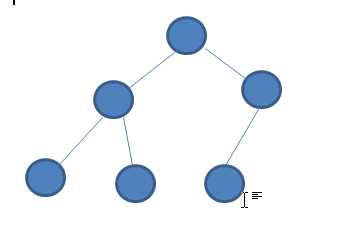
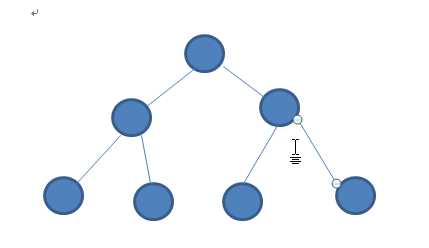
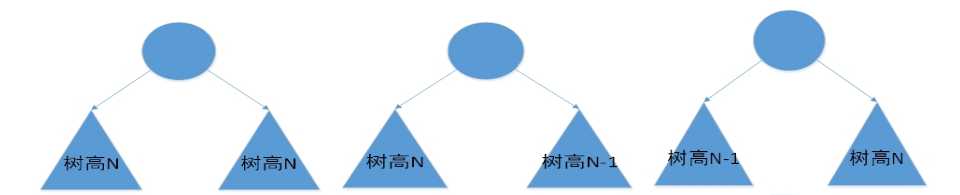
二叉树的基本性质

(1) 在非空二叉树中，第i层的结点总数不超过  , i>=1；

(2) 深度为h的二叉树最多有 个结点(h>=1)，最少有h个结点；

(4) 具有n个结点的完全二叉树的深度为

二叉树的遍历

对于二叉树来讲最主要、最基本的运算是遍历。 

从二叉树的递归定义可知，一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此，在任一给定结点上，可以按某种次序执行三个操作： 
　（1）访问结点本身(N)， 
　（2）遍历该结点的左子树(L)， 
　（3）遍历该结点的右子树(R)。 

遍历方法普遍有以下几种：

先序遍历（NLR）、中序遍历（LNR），后序遍历（LRN）和层次遍历。

遍历节点顺序：

        先序遍历（NLR）：根、左子树、右子树

　　 中序遍历（LNR）：左子树、根、右子树

　　 后序遍历（LRN）：左子树、右子树、根

　　 层次遍历：按照从上到下、从左到右的次序进行遍历

二叉树的代码的实现

二叉树的用途

（有待更新）

二叉树原理和作用，总结

标签：用途   技术分享   原理   中序   abs   操作   ddb   static   部分   

原文地址：http://www.cnblogs.com/wwjchina/p/7749556.html