标签：条件 src 树形背包 安装 gif com 这一 [1] print
最近一直在填坑练树形DP，练到树包这一块，然后就开始打[BZOJ4753 最佳团体]
打这道题之前刚刚打了[BZOJ2427 软件安装]，是个有依赖的树形背包，这道题思路也比较相似，就码码码，天真的把 f 数组记录了两维，然后转移的时候硬除下来比较
我还是太年轻了QAQ
Maple神犇上来就说出了01分数规划这种神奇的操作。但是这种操作我原来只是听说过，现在来学习一下，也是非常简单的啊
所谓01分数规划，那么当然要有分数
一般是解决此类问题的：有一堆物品，每一个物品有一个收益ai，一个代价bi，我们要求一个方案使选择的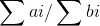
最大
我们是可以二分答案x的，这样对于每个答案，就有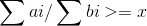
变形得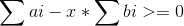
，这样我们就可以把每个物品的权值变为 ai-x*bi，然后再按照题意搞，搞出来的结果如果满足>=0这个条件，意味着还可能存在最优解，于是继续二分下去就好啦
01分数规划通常有这么几种：
（1）基础应用
就像上面这种选物品的，当然也可能加一些改动，比如说只让选n-k个物品啊，只要排一遍序取前n-k个，求和与0比较就好啦
相关例题：poj2976
（2）与其他算法结合
①与动规等结合
就是我刚刚做的那个就是与树形有依赖背包结合的01分数规划 BZOJ4753
#include<iostream>
#include<cstdio>
#include<cstring>
#define pos(i,a,b) for(int i=(a);i<=(b);i++)
#define pos2(i,a,b) for(int i=(a);i>=(b);i--)
#define N 2511
#define LL long long
using namespace std;
const double eps=1e-5;
struct haha{
int next,to;
}edge[N*10];
int head[N],cnt=1;
void add(int u,int v){
edge[cnt].to=v;
edge[cnt].next=head[u];
head[u]=cnt++;
}
int n,m,w[N],v[N];
double f[N][N],wei[N];
int out[N],size[N];
double l,r;
void dfs(int x){
size[x]=1;f[x][0]=0;
if(out[x]==0){
f[x][1]=wei[x];
return;
}
for(int i=head[x];i;i=edge[i].next){
int to=edge[i].to;
dfs(to);
int mi=min(m,size[x]);
pos2(j,mi,0){
pos(k,0,size[to]){
if(j+k>m) break;
f[x][j+k]=max(f[x][j+k],f[x][j]+f[to][k]);
}
}size[x]+=size[to];
}
pos2(i,m,0){
if(i>=1){
f[x][i]=f[x][i-1]+wei[x];
}
else f[x][i]=0;
}
}
int check(double num){
pos(i,1,n) wei[i]=(double)v[i]-num*(double)w[i];
pos(i,1,n) pos(j,1,n) f[i][j]=-100000000;
dfs(1);
if(f[1][m]>-eps) return 1;
return 0;
}
int main(){
scanf("%d%d",&m,&n);n++;m++;
pos(i,2,n){
int x;scanf("%d%d%d",&w[i],&v[i],&x);
x++;add(x,i);out[x]++;
}
r=10000;
while(l+eps<r){
double mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%.3lf",l);
return 0;
}
②与最小生成树结合：最优比率生成树
比如：
给出一个n个点的完全图，每条边有两个权值cost和len。我们求一个生成树使得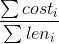
最小
还是二分答案x，把每条边边权设为cost-x*len，跑最小生成树，判答案的正负再去二分
例题：poj2728
③与最短路结合：最优比率生成环
比如：
给出一个有L个点P条边的有向图，每个点上有点权F，每条边上有边权T。求一个回路使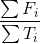
最大
因为环上边和点数相等，我们可以直接把边权当做花费，入点的点权当作收入。
然后还是二分答案建图，判图中有没有正环。这里我们可以用一个技巧，我们建权值的时候取反，然后用spfa判负环就好啦。
例题：poj3621
后边两种结合我懒也就没打QAQ，其实懂了打一道练练就好说了。等我有时间（如果的话）一定把后两道题代码补上2333
标签：条件 src 树形背包 安装 gif com 这一 [1] print
原文地址：http://www.cnblogs.com/Hallmeow/p/7750483.html
