假定为预测房价的例子，自变量为面积，房间数两个，因变量为房价。

那么可以得到的公式为：

其中代表房间数，代表变量前面的系数。

其中代表面积，代表变量前面的系数。

首先我们祭出两张图代表数据是否均一化的最优解寻解过程。

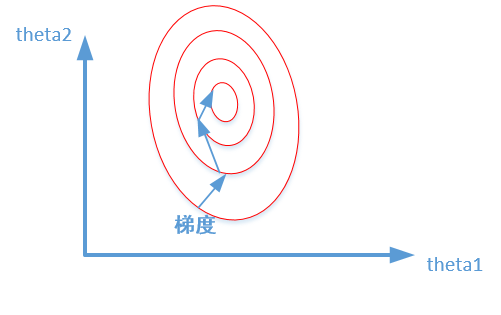
未归一化：

归一化之后

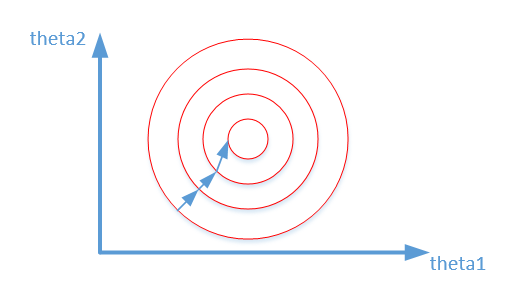
为什么会出现上述两个图，并且它们分别代表什么意思。

我们在寻找最优解的过程也就是在使得损失函数值最小的theta1,theta2。

上述两幅图代码的是损失函数的等高线。

我们很容易看出，当数据没有归一化的时候，面积数的范围可以从0~1000，房间数的范围一般为0~10，可以看出面积数的取值范围远大于房间数。

影响

这样造成的影响就是在画损失函数的时候，

数据没有归一化的表达式，可以为：

造成图像的等高线为类似椭圆形状，最优解的寻优过程就是像下图所示：

而数据归一化之后，损失函数的表达式可以表示为：

其中变量的前面系数几乎一样，则图像的等高线为类似圆形形状，最优解的寻优过程像下图所示：

从上可以看出，数据归一化后，最优解的寻优过程明显会变得平缓，更容易正确的收敛到最优解。