标签：port 参数 set 平均值 决策树 ast process 逻辑 ack
感谢中国人民大学胡鹤老师，课程深入浅出，非常好
关于SVM
可以做线性分类、非线性分类、线性回归等，相比逻辑回归、线性回归、决策树等模型（非神经网络）功效最好
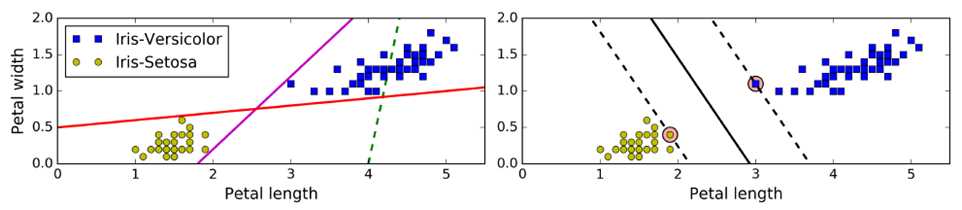
传统线性分类：选出两堆数据的质心，并做中垂线（准确性低）——上图左
SVM：拟合的不是一条线，而是两条平行线，且这两条平行线宽度尽量大，主要关注距离车道近的边缘数据点（支撑向量support vector），即large margin classification——上图右
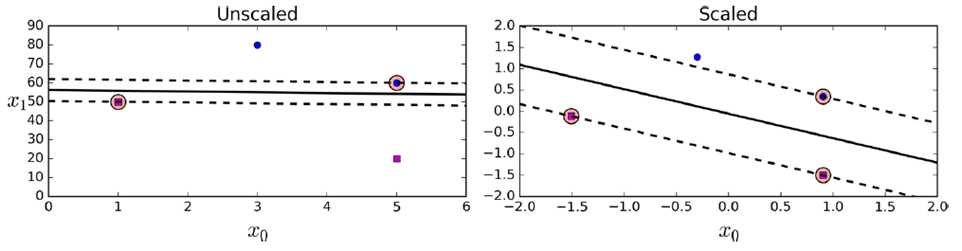
使用前，需要对数据集做一个scaling，以做出更好的决策边界（decision boundary）
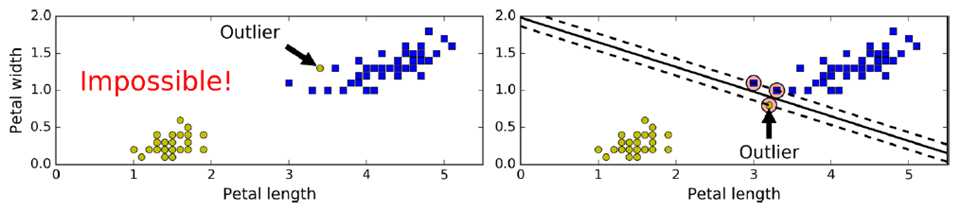
但需要容忍一些点跨越分割界限，提高泛化性，即softmax classification
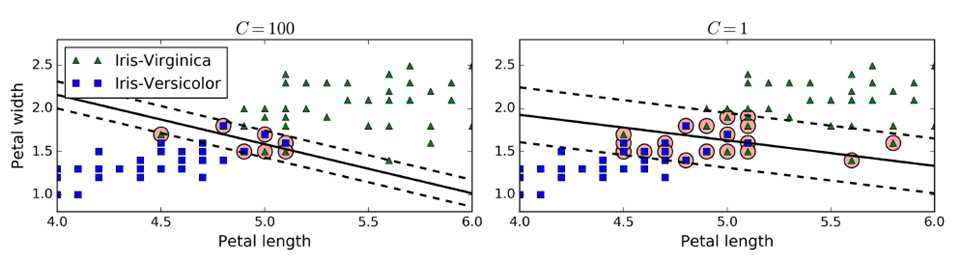
在sklearn中，有一个超参数c，控制模型复杂度，c越大，容忍度越小，c越小，容忍度越高。c添加一个新的正则量，可以控制SVM泛化能力，防止过拟合。（一般使用gradsearch）
SVM特有损失函数Hinge Loss
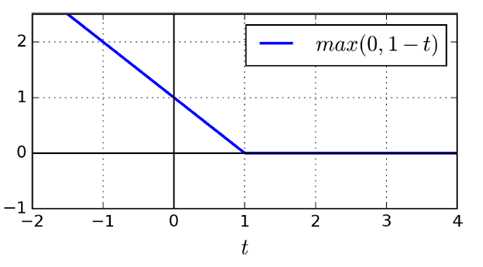
LinearSVC(liblinear库，不支持kernel函数，但是相对简单，复杂度O(m*n)）
同SVM特点吻合，仅考虑落在分类面附近和越过分类面到对方领域的向量，给于一个线性惩罚（l1），或者平方项（l2）
import numpy as np from sklearn import datasets from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler from sklearn.svm import LinearSVC iris = datasets.load_iris() X = iris["data"][:,(2,3)] y = (iris["target"]==2).astype(np.float64) svm_clf = Pipeline(( ("scaler",StandardScaler()), ("Linear_svc",LinearSVC(C=1,loss="hinge")), )) svm_clf.fit(X,y) print(svm_clf.predit([[5.5,1.7]]))
对于nonlinear数据的分类
有两种方法，构造高维特征，构造相似度特征
使用高维空间特征（即kernel的思想），将数据平方、三次方。。映射到高维空间上
from sklearn.preprocessing import PolynomialFeatures polynomial_svm_clf = Pipeline(( ("poly_features", PolynomialFeatures(degree=3)), ("scaler", StandardScaler()), ("svm_clf", LinearSVC(C=10, loss="hinge")) )) polynomial_svm_clf.fit(X, y)
这种kernel trick可以极大地简化模型，不需要显示的处理高维特征，可以计算出比较复杂的情况
但模型复杂度越强，过拟合风险越大
SVC（基于libsvm库，支持kernel函数，但是相对复杂，不能用太大规模数据，复杂度O(m^2 *n)-O(m^3 *n)）
可以直接使用SVC（coef0：高次与低次权重）
from sklearn.svm import SVC poly_kernel_svm_clf = Pipeline(( ("scaler", StandardScaler()), ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5)) )) poly_kernel_svm_clf.fit(X, y)
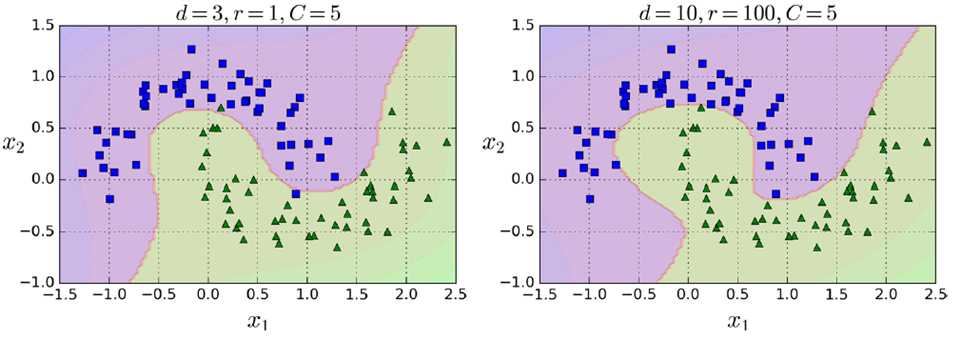
添加相似度特征（similarity features）
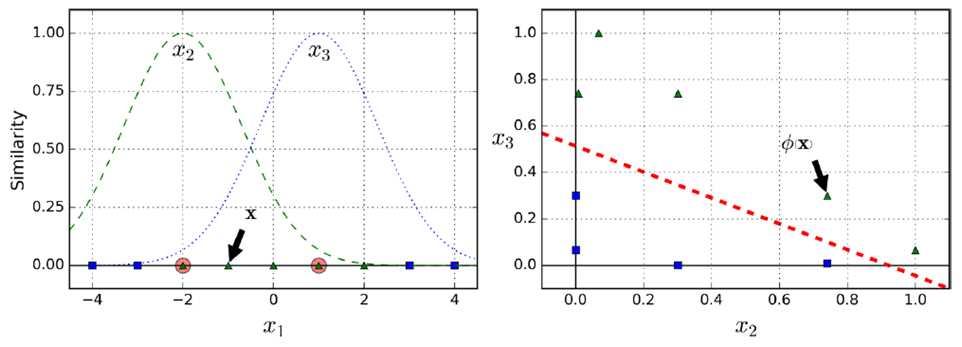
例如，下图分别创造x1,x2两点的高斯分布，再创建新的坐标系统，计算高斯距离（Gaussian RBF Kernel径向基函数）
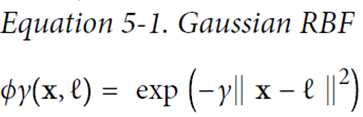
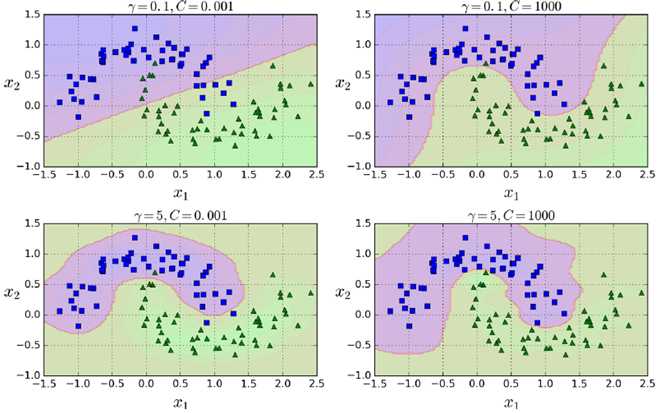
gamma（γ）控制高斯曲线形状胖瘦，数据点之间的距离发挥更强作用
rbf_kernel_svm_clf = Pipeline(( ("scaler", StandardScaler()), ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001)) )) rbf_kernel_svm_clf.fit(X, y)
如下是不同gamma和C的取值影响
SGDClassifier(支持海量数据，时间复杂度O(m*n))
SVM Regression（SVM回归）
尽量让所用instance都fit到车道上，车道宽度使用超参数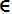
控制，越大越宽
使用LinearSVR
from sklearn.svm import LinearSVR svm_reg = LinearSVR(epsilon=1.5) svm_reg.fit(X, y)
使用SVR
from sklearn.svm import SVR svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1) svm_poly_reg.fit(X, y)
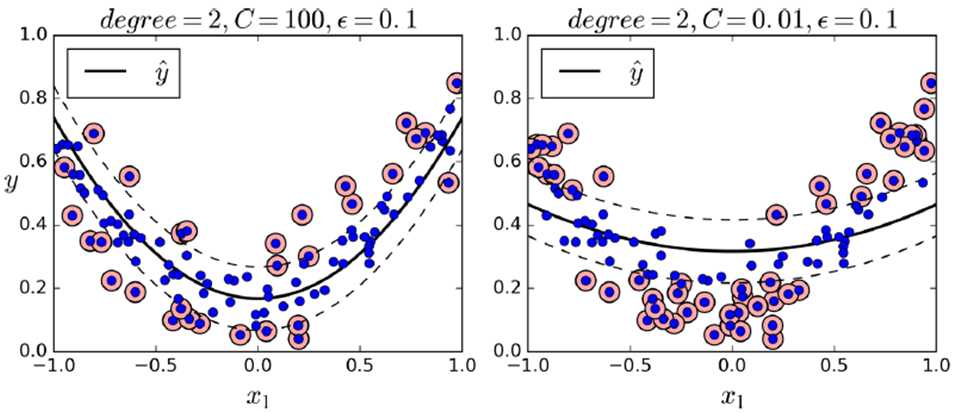
数学原理：
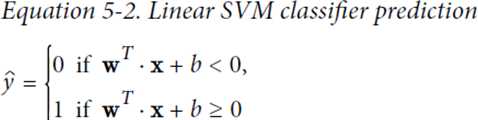
w通过控制h倾斜的角度，控制车道的宽度，越小越宽，并且使得违反分类的数据点更少
hard margin linear SVM
优化目标：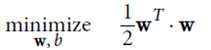
，并且保证
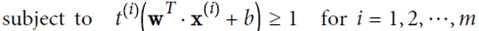
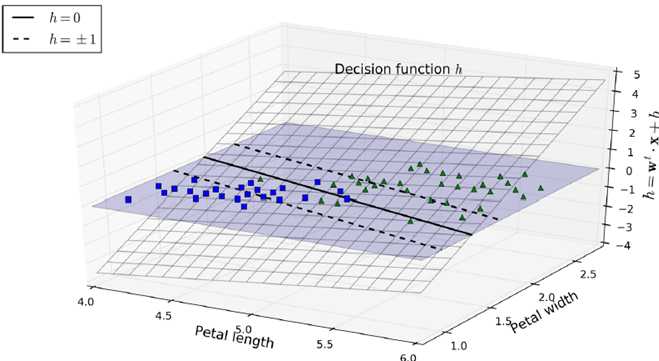
soft margin linear SVM
增加一个新的松弛变量（slack variable）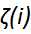
，起正则化作用
优化目标：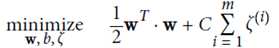
，并且保证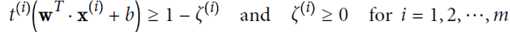
放宽条件，即使有个别实例违反条件，也惩罚不大
LinearSVM
使用拉格朗日乘子法进行计算，α是松弛项后的结果
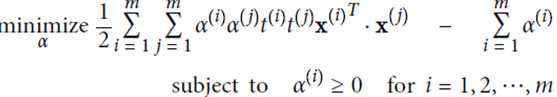
计算结果：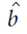
取平均值
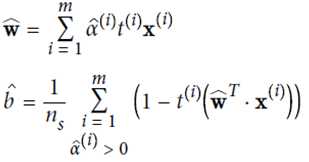
KernelizedSVM
由于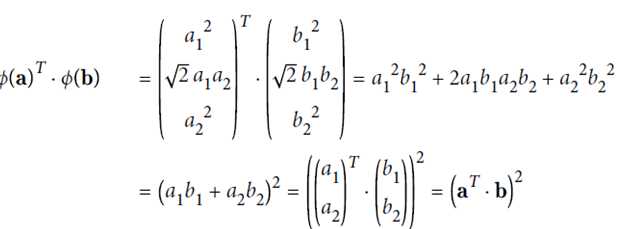
故可先在低位空间里做点积计算，再映射到高维空间中。
下列公式表示，在高维空间计算可用kernel trick方式，直接在低维上面计算
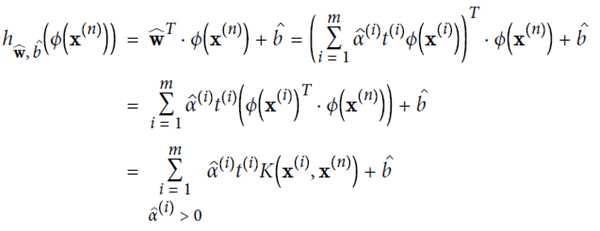
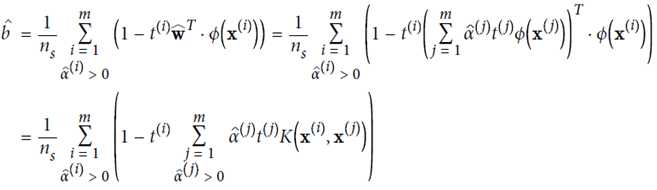
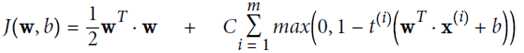
几个常见的kernal及其function
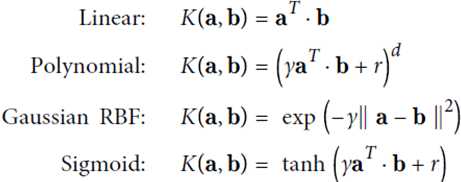
标签：port 参数 set 平均值 决策树 ast process 逻辑 ack
原文地址：http://www.cnblogs.com/rucwxb/p/7753330.html
