标签:break space highlight 最大 amp noip2009 png cst com
题目:洛谷P1074、Vijos P1755、codevs1174。
题目大意:给你一个数独,让你填完这个数独,并要求得分最大,问这个得分是多少(不能填完输出-1)。
每个格子的得分是当前格子所填的数乘格子的分值。
格子的分值如下: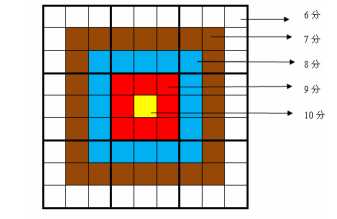
解题思路:暴力搜索。
然而不加优化的搜索是一定会超时的。
我用了这几个优化就过了这道题:
①位运算,用一个九位二进制数来保存每行/列/九宫格中已经用过的数字,则对于一个点,不能用的数字就是它所在行的状态or列的状态or九宫格的状态。
②每次搜索时,找一个能填的数字最少的格子进行搜索。
③register和手动O2(逃
之后只要你不像我一样把求最大值看成最小值,就能AC了。
C++ Code:
#include<cstdio>
using namespace std;
int nin[10][10]={{0},
{0,1,1,1,2,2,2,3,3,3},
{0,1,1,1,2,2,2,3,3,3},
{0,1,1,1,2,2,2,3,3,3},
{0,4,4,4,5,5,5,6,6,6},
{0,4,4,4,5,5,5,6,6,6},
{0,4,4,4,5,5,5,6,6,6},
{0,7,7,7,8,8,8,9,9,9},
{0,7,7,7,8,8,8,9,9,9},
{0,7,7,7,8,8,8,9,9,9}
},sco[10][10]={{0},
{0,6,6,6,6,6,6,6,6,6},
{0,6,7,7,7,7,7,7,7,6},
{0,6,7,8,8,8,8,8,7,6},
{0,6,7,8,9,9,9,8,7,6},
{0,6,7,8,9,10,9,8,7,6},
{0,6,7,8,9,9,9,8,7,6},
{0,6,7,8,8,8,8,8,7,6},
{0,6,7,7,7,7,7,7,7,6},
{0,6,6,6,6,6,6,6,6,6},
};
int sd[10][10],hang[10]={0},lie[10]={0},kuai[10]={0},ans;
__attribute__((optimize("-O2")))void dfs(int s,int p){
if(p==81){
if(ans<s)ans=s;
return;
}
int x,y,mn=0x3f3f3f3f;
for(register int i=1;i<=9;++i){
for(register int j=1;j<=9;++j)
if(!sd[i][j]){
int t=hang[i]|lie[j]|kuai[nin[i][j]],js=0;
for(register int k=0;k<9;++k)
js+=!(t&(1<<k));
if(js<mn)mn=js,x=i,y=j;
if(js==1)break;
}
if(mn==1)break;
}
if(mn==0x3f3f3f3f)return;
int t=hang[x]|lie[y]|kuai[nin[x][y]];
for(register int k=9;k;--k)
if(!(t&(1<<(k-1)))){
int f=1<<(k-1);
hang[x]^=f;
lie[y]^=f;
sd[x][y]=k;
kuai[nin[x][y]]^=f;
dfs(s+sco[x][y]*k,p+1);
hang[x]^=f;
sd[x][y]=0;
lie[y]^=f;
kuai[nin[x][y]]^=f;
}
}
int main(){
ans=-1;
int s=0,p=0;
for(int i=1;i<=9;++i){
for(int j=1;j<=9;++j){
int& now=sd[i][j];
scanf("%d",&now);
if(now)s+=now*sco[i][j],++p,hang[i]|=1<<(now-1),lie[j]|=1<<(now-1),kuai[nin[i][j]]|=1<<(now-1);
}
}
dfs(s,p);
printf("%d\n",ans);
return 0;
}
标签:break space highlight 最大 amp noip2009 png cst com
原文地址:http://www.cnblogs.com/Mrsrz/p/7762674.html