题目描述
出题是一件痛苦的事情!
题目看多了也有审美疲劳,于是我舍弃了大家所熟悉的A+B Problem,改用A-B了哈哈!
好吧,题目是这样的:给出一串数以及一个数字C,要求计算出所有A-B=C的数对的个数。(不同位置的数字一样的数对算不同的数对)
输入输出格式
输入格式:第一行包括2个非负整数N和C,中间用空格隔开。
第二行有N个整数,中间用空格隔开,作为要求处理的那串数。
输出格式:输出一行,表示该串数中包含的所有满足A-B=C的数对的个数。
输入输出样例
说明
对于90%的数据,N <= 2000;
对于100%的数据,N <= 200000。
所有输入数据都在longint范围内。
解题思路
- 对于90%的数据,容易得出我们可以直接用两重for循环暴力枚举求得,复杂度为O(N2)
- 即:
- 而对于100%的数据,N高达200000.
- 做题的时候并没有什么想法,只是想到要不排序一遍?然后再阉割一下这个数列,减少一下循环次数?
- 深入考虑又发现了这个思路的不可做性
- 于是转而考虑用一个桶的思想
- 考虑将每个读入的数计入,再考虑一个数+C是否有出现(即有被计数)
- 如果有即证明已经存在一对数
- 那么只需要O(N)扫描一遍即可
- 总体复杂度O(N)
关于代码

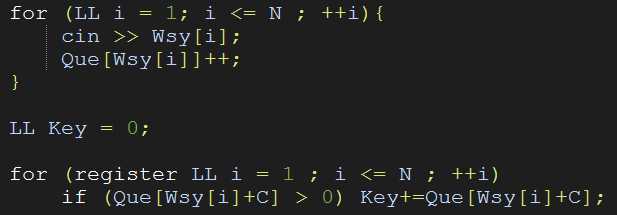
1 #include <bits/stdc++.h> 2 #define LL long long 3 4 using namespace std; 5 6 LL Read() 7 { 8 LL val = 0, opt = 1; 9 char ch; 10 while (!(isdigit( ch = getchar() ) || ch == ‘-‘)); 11 if (ch == ‘-‘) opt =-1; 12 else val = ch - ‘0‘; 13 while (isdigit( ch = getchar() )) (val *= 10) += ch - ‘0‘; 14 return val * opt; 15 } 16 17 map <LL , LL> Que; 18 LL Wsy[200222]; 19 int main() 20 { 21 22 ios::sync_with_stdio(0); 23 24 LL N , C; 25 N = Read(); 26 C = Read(); 27 for (LL i = 1; i <= N ; ++i){ 28 cin >> Wsy[i]; 29 Que[Wsy[i]]++; 30 } 31 32 LL Key = 0; 33 34 for (register LL i = 1 ; i <= N ; ++i) 35 if (Que[Wsy[i]+C] > 0) Key+=Que[Wsy[i]+C]; 36 37 cout << Key; 38 39 return 0; 40 }
解题思路
关于代码
 A-B
A-B