《神经网络与深度学习》（三） 稀疏编码

标签：em算法   样本   建模   情况下   矩阵   logistic   over   优化   组合   

转自：http://www.cnblogs.com/caocan702/p/5666175.html

借鉴前人的文章链接

http://blog.csdn.net/zouxy09/article/details/8777094

http://www.gene-seq.com/bbs/thread-2853-1-1.html

http://ibillxia.github.io/blog/2012/09/26/convex-optimization-overview/

UFLDL教程

http://ufldl.stanford.edu/wiki/index.php/%E7%A8%80%E7%96%8F%E7%BC%96%E7%A0%81

如果我们把输出必须和输入相等的限制放松，同时利用线性代数中基的概念，即O = a₁*Φ₁ + a₂*Φ₂+….+ a_n*Φ_n， Φ_i是基，a_i是系数，我们可以得到这样一个优化问题：

Min |I – O|，其中I表示输入，O表示输出。

通过求解这个最优化式子，我们可以求得系数a_i和基Φ_i，这些系数和基就是输入的另外一种近似表达。

因此，它们可以用来表达输入I，这个过程也是自动学习得到的。如果我们在上述式子上加上L1的Regularity限制，得到：

Min |I – O| + u*(|a₁| + |a₂| + … + |a_n |)

这种方法被称为Sparse Coding。通俗的说，就是将一个信号表示为一组基的线性组合，而且要求只需要较少的几个基就可以将信号表示出来。“稀疏性”定义为：只有很少的几个非零元素或只有很少的几个远大于零的元素。要求系数 a_i 是稀疏的意思就是说：对于一组输入向量，我们只想有尽可能少的几个系数远大于零。选择使用具有稀疏性的分量来表示我们的输入数据是有原因的，因为绝大多数的感官数据，比如自然图像，可以被表示成少量基本元素的叠加，在图像中这些基本元素可以是面或者线。同时，比如与初级视觉皮层的类比过程也因此得到了提升（人脑有大量的神经元，但对于某些图像或者边缘只有很少的神经元兴奋，其他都处于抑制状态）。

稀疏编码算法是一种无监督学习方法，它用来寻找一组“超完备”基向量来更高效地表示样本数据。虽然形如主成分分析技术（PCA）能使我们方便地找到一组“完备”基向量，但是这里我们想要做的是找到一组“超完备”基向量来表示输入向量（也就是说，基向量的个数比输入向量的维数要大）。超完备基的好处是它们能更有效地找出隐含在输入数据内部的结构与模式。然而，对于超完备基来说，系数a_i不再由输入向量唯一确定。因此，在稀疏编码算法中，我们另加了一个评判标准“稀疏性”来解决因超完备而导致的退化（degeneracy）问题。

比如在图像的Feature Extraction的最底层要做Edge Detector的生成，那么这里的工作就是从Natural Images中randomly选取一些小patch，通过这些patch生成能够描述他们的“基”，也就是右边的8*8=64个basis组成的basis，然后给定一个test patch, 我们可以按照上面的式子通过basis的线性组合得到，而sparse matrix就是a，下图中的a中有64个维度，其中非零项只有3个，故称“sparse”。

Sparse coding分为两个部分：

1）Training阶段：给定一系列的样本图片[x1, x 2, …]，我们需要学习得到一组基[Φ1, Φ2, …]，也就是字典。

稀疏编码是k-means算法的变体，其训练过程也差不多（EM算法的思想：如果要优化的目标函数包含两个变量，如L(W, B)，那么我们可以先固定W，调整B使得L最小，然后再固定B，调整W使L最小，这样迭代交替，不断将L推向最小值。

训练过程就是一个重复迭代的过程，按上面所说，我们交替的更改a和Φ使得下面这个目标函数最小。

每次迭代分两步：

a）固定字典Φ[k]，然后调整a[k]，使得上式，即目标函数最小（即解LASSO问题）。见下

b）然后固定住a [k]，调整Φ [k]，使得上式，即目标函数最小（即解凸QP问题）。见下

不断迭代，直至收敛。这样就可以得到一组可以良好表示这一系列x的基，也就是字典。

2）Coding阶段：给定一个新的图片x，由上面得到的字典，通过解一个LASSO问题得到稀疏向量a。这个稀疏向量就是这个输入向量x的一个稀疏表达了。

例如：

LASSO问题

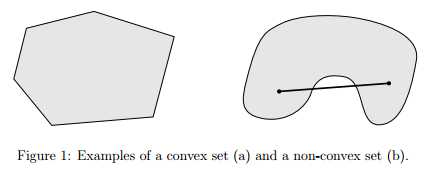
常见的凸集有：n维实数空间；一些范数约束形式的集合；仿射子空间；凸集的并集；n维半正定矩阵集；凸优化中的一个核心概念就是凸函数。

凸函数定义：一个函数f:Rn→R是凸函数当且仅当其定义域（设为D(f)）是凸集， 且对任意的x,y∈D(f)和θ∈R且0≤θ≤1，都有

f(θx+(1?θ)y≤θf(x)+(1?θ)f(y))

 

设f(x)为一元函数，那么上式的几何意义在于，曲线上任意两点处的割线在函数曲线的上方，常见的凸函数有指数函数（f(x)=ax，a>1）、负对数函数（f(x)=?logax，a>1，x>0）、开口向上的二次函数等。

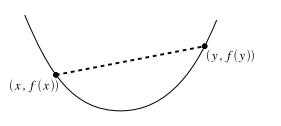
有了凸集和凸函数的定义，现在我们重点讨论凸优化问题的求解方法。凸优化的一般描述为：

其中f(x)为凸函数，C是一个凸集，这是不带约束条件的情况下的凸优化问题。对于带约束条件的问题而言，其一般描述为：
其中f(x)为凸函数，gi(x)对所有的ii均为凸函数，hj(x)均为仿射函数。注意gi(x)不等式中不等号的方向。

 

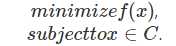
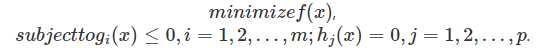
凸问题中的全局优化：首先要分清楚什么是局部最优，什么是全局最优。局部最优是指在该最优值附近的点对应的函数值 都比该最优值大，而全局最优是指对可行域里所有点，其函数值都比该最优值大。对于凸优化问题，它具有一个很重要的特性， 那就是所有的局部最优值都是全局最优的。

（1）线性规划（Linear Programing, LP）: 目标函数和约束条件函数都是线性函数的情况，一般形式如下：

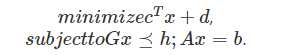
（2）二次规划（Quadratic Programing, QP）: 目标函数为二次函数，约束条件为线性函数，一般形式为：

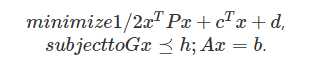
LP可以看做是QP的特例，QP包含LP。

（3）二次约束的二次规划（Quadratically Constrained Quadratic Programming, QCQP）: 目标函数和约束条件均为 二次函数的情况，QP可以看做是QCQP的特例，QCQP包含QP。

（4）半正定规划（Semide?nite Programming，SDP）QCQP可以看做是SDP的特例，SDP包含QCQP。SDP在machine learning中有非常广泛的应用。

凸优化应用举例

下面我们来看几个实例。
（1）支持向量机（Support Vector Machines，SVM）：凸优化在machine learning中的一个典型的应用就是基于支持向量机分类器， 它可以用如下优化问题表示：

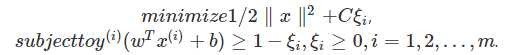
其中决策变量w∈Rn,ξ∈Rn,b∈R. C∈R,x(i),y(i),i=1,2,…,m由 具体问题定义。可以看出，这是一个典型的QP问题。

（2）带约束的least squares问题：其一般描述为

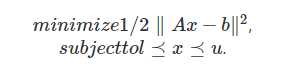
这也是一个很典型的QP问题。

（3）Maximum Likelihood for Logistic Regression：该问题的目标函数为:其中g(z)g(z)为Sigmoid函数，

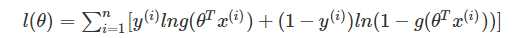
对于凸优化问题，目前没有一个通用的解析式的 解决方案，但是我们仍然可以用非解析的方法来有效的求解很多问题。内点法被证明是很好的解决方案， 特别具有实用性，在某些问题中，能够在多项式时间复杂度下，将解精确到指定精度。

《神经网络与深度学习》（三） 稀疏编码

标签：em算法   样本   建模   情况下   矩阵   logistic   over   优化   组合   

原文地址：http://www.cnblogs.com/flippedkiki/p/7765721.html