标签:obj utils open multi file cti none 导入 arrays
When SciPy is built using the optimized ATLAS LAPACK and BLAS libraries, it has very fast linear algebra capabilities.
If you dig deep enough, all of the raw lapack and blas libraries are available for your use for even more speed.
All of these linear algebra routines expect an object that can be converted into a 2-dimensional array. The output of these routines is also a two-dimensional array.

NAME
numpy.linalg
DESCRIPTION
Core Linear Algebra Tools
-------------------------
Linear algebra basics:
- norm Vector or matrix norm
- inv Inverse of a square matrix
- solve Solve a linear system of equations
- det Determinant of a square matrix
- lstsq Solve linear least-squares problem
- pinv Pseudo-inverse (Moore-Penrose) calculated using a singular
value decomposition
- matrix_power Integer power of a square matrix
Eigenvalues and decompositions:
- eig Eigenvalues and vectors of a square matrix
- eigh Eigenvalues and eigenvectors of a Hermitian matrix
- eigvals Eigenvalues of a square matrix
- eigvalsh Eigenvalues of a Hermitian matrix
- qr QR decomposition of a matrix
- svd Singular value decomposition of a matrix
- cholesky Cholesky decomposition of a matrix
Tensor operations:
- tensorsolve Solve a linear tensor equation
- tensorinv Calculate an inverse of a tensor
Exceptions:
- LinAlgError Indicates a failed linear algebra operation

LA.info?
Type: module
String form: <module ‘numpy.linalg.info‘ from ‘F:\\Anaconda3\\lib\\site-packages\\numpy\\linalg\\info.py‘>
File: f:\anaconda3\lib\site-packages\numpy\linalg\info.py
Docstring:
Core Linear Algebra Tools
-------------------------
Linear algebra basics:
- norm Vector or matrix norm
- inv Inverse of a square matrix
- solve Solve a linear system of equations
- det Determinant of a square matrix
- lstsq Solve linear least-squares problem
- pinv Pseudo-inverse (Moore-Penrose) calculated using a singular
value decomposition
- matrix_power Integer power of a square matrix
Eigenvalues and decompositions:
- eig Eigenvalues and vectors of a square matrix
- eigh Eigenvalues and eigenvectors of a Hermitian matrix
- eigvals Eigenvalues of a square matrix
- eigvalsh Eigenvalues of a Hermitian matrix
- qr QR decomposition of a matrix
- svd Singular value decomposition of a matrix
- cholesky Cholesky decomposition of a matrix
Tensor operations:
- tensorsolve Solve a linear tensor equation
- tensorinv Calculate an inverse of a tensor
Exceptions:
- LinAlgError Indicates a failed linear algebra operation
‘bench‘,‘cholesky‘,‘cond‘,‘det‘,‘division‘,‘eig‘,‘array‘,‘eigh‘,‘eigvals‘,‘eigvalsh‘,‘info‘,‘inv‘,‘lapack_lite‘,‘linalg‘,‘lstsq‘,‘matrix_power‘,‘matrix_rank‘,‘multi_dot‘,‘norm‘,‘pinv‘,‘print_function‘,‘qr‘,‘slogdet‘,‘solve‘,‘svd‘,‘tensorinv‘,‘tensorsolve‘,‘test‘
eig : eigenvalues and right eigenvectors of general arrays
eigvalsh : eigenvalues of symmetric or Hermitian arrays.
eigh : eigenvalues and eigenvectors of symmetric/Hermitian arrays.
首先导入相关模块
import numpy as np from scipy import linalg as LA #or #from numpy import linalg as LA
3.1求数组的行列式:det

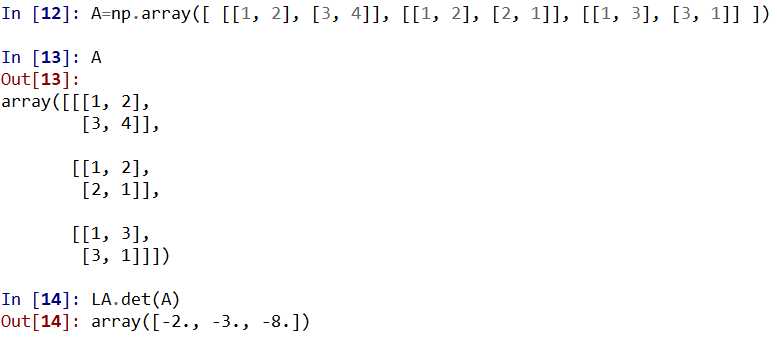
3.2求方阵的特征值、特征向量:eig

3.3求方阵的逆矩阵::inv


3.4求解线性方程组:solve
Solve the system of equations 3 * x0 + x1 = 9 and x0 + 2 * x1 = 8:

3.5一个方阵的整数次幂:matrix_power


3.6计算在一个函数调用两个或两个以上的阵列的点积:multi_dot

https://docs.scipy.org/doc/numpy/reference/routines.linalg.html
标签:obj utils open multi file cti none 导入 arrays
原文地址:http://www.cnblogs.com/jasonhaven/p/7777712.html