标签:进制 动态 哪些 sizeof inline city 2.0 while algo
T1不难,
原图是一棵满二叉树
一定连通
通过两端点的编号二进制可以找到LCA
LCA = 两端点编号二进制串的最长公共前缀
之后易计算距离
T2期望直接不懂,需要花一天时间学一下期望,
不让要是真的出了关于期望的题,可别读不懂题目。
N=1, Li=Ri,即只有一张画纸
动态规划计算K次操作后最后呈现出每种颜色的概率
F[i][j]表示涂色i次后显示颜色j的概率
转移时枚举t,表示刷上颜色t
F[i+1][j*t%c] += F[i][j]/c
G[i][j]表示i次被包含在区间里,j次被选中的概率
G[i][j] = C(i,j)/2i = (G[i-1][j]+G[i-1][j-1])/2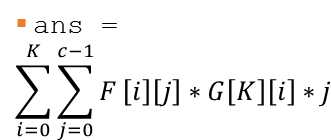
和的期望=期望的和
无论区间长短,区间内每个被覆盖到的画纸都有1/2的概率被选中上色
对每张画纸单独计算,统计被多少个区间覆盖
用和之前一样的方法计算每张画纸最后的期望
T3
状态压缩DP
Floyd预处理两两之间最短路,并预处理:
F[i][sta]表示从家开始,当前走到点i,已经走过sta中的点,走过的最短距离是多少
G[i][sta]表示从花店开始,当前走到点i,已经走过sta中的点,走过的最短距离是多少
枚举先收割哪些花田,记为A,其余的花田记为B
分交货前和交货后两段,单独计算最短距离。以交货前为例:
枚举A中最后一个收割的点i、B中第一个收割的点j
求min{F[i][A]+dis(i,j)+G[j][B]}
T1三向城
/* 这道题应该不难,画个图就出来了嘛,再GG可就没救了 */ #include <iostream> #include <cstdio> #include <algorithm> #include <cmath> #include <cstring> #include <string> using namespace std; inline int read(){ int x = 0; char c = getchar(); while(c < ‘0‘ || c > ‘9‘) c = getchar(); while(c >= ‘0‘ && c <= ‘9‘) x = x * 10 + c - ‘0‘, c = getchar(); return x; } int a[60]; int main() { freopen("city.in", "r", stdin); freopen("city.out", "w", stdout); int T = read(); while(T --){ int x = read(); int y = read(); if(x == 0 || y == 0){ printf("-1\n"); continue ; } if(x == y){ printf("0\n"); continue ; } int js = 0; a[0] = x; while(x){ a[++ js] = x / 2; x /= 2; } bool flag = 1; int ans = 0; while(y && flag){ for(int i = 0; flag && i < js; i ++) if(y == a[i]){ printf("%d\n", i + ans); flag = 0; } ans ++; y /= 2; } if(flag) printf("-1\n"); } return 0; } /* 3 5 7 2 4 1 1 */
T2灵魂画师
#include <cstdio> #include <cstring> #define eps 1e-9 int k,n,T,i,j,c,K,x,y,mx,cnt[105]; double g[105][105],f[105][105],ans; int main() { freopen("paint.in", "r", stdin); freopen("paint.out", "w", stdout); g[0][0] = 1; for (i=0; i<100; ++i) for (j=0; j<=i; ++j) { g[i+1][j] += g[i][j]/2.0; g[i+1][j+1] += g[i][j]/2.0; } scanf("%d%d%d", &n, &c, &K); mx = 0; memset(cnt, 0, sizeof cnt); for (i=1; i<=K; ++i) { scanf("%d%d", &x, &y); for (j=x; j<=y; ++j) { ++cnt[j]; if (cnt[j] > mx) mx = cnt[j]; } } memset(f, 0, sizeof f); f[0][1] = 1; for (i=0; i<mx; ++i) for (j=0; j<c; ++j) if (f[i][j] > eps) for (k=0; k<c; ++k) f[i+1][j*k%c] += f[i][j]/c; ans = 0; for (i=1; i<=n; ++i) for (j=0; j<=cnt[i]; ++j) for (k=0; k<c; ++k) ans += g[cnt[i]][j]*f[j][k]*k; printf("%.3lf\n", ans); return 0; }
T3香子兰
#include <cstdio> #define inf 1000000007 #define N 24 int a[N][N],d[N][N],f[2][N][1050000],e[N],cnt[1050000],n,n1,n2,x,y,z,i,j,m,k,q,ans,sta; int main() { freopen("vanilla.in", "r", stdin); freopen("vanilla.out", "w", stdout); e[0] = 1; //预处理2^i for (i=1; i<=22; ++i) e[i] = e[i-1]<<1; //预处理每个二进制数中有几个1 for (i=0; i<e[20]; ++i) for (x=i; x!=0; x>>=1) cnt[i] += x&1; scanf("%d%d", &n, &m); for (i=1; i<=n; ++i) for (j=1; j<=n; ++j) d[i][j] = inf*(i!=j); for (i=1; i<=m; ++i) { scanf("%d%d%d", &x, &y, &z); ++x; ++y; if (z<d[x][y]) d[x][y] = d[y][x] = z; } // floyd求两两最短路 for (k=1; k<=n; ++k) for (i=1; i<=n; ++i) for (j=1; j<=n; ++j) if (d[i][k]+d[k][j] < d[i][j]) d[i][j] = d[i][k]+d[k][j]; if (n == 3) { printf("%d\n", (d[1][2]+d[2][3])*2); return 0; } n1 = (n-2)/2; n2 = n-2-n1; //求从家、花店开始,走到点i,经过的点为j的最短路 //q=0:从家开始,q=1:从花店开始 for (q=0; q<=1; ++q) { //初始化状态 for (i=1; i<=n; ++i) for (j=0; j<e[n-2]; ++j) f[q][i][j] = inf; if (q == 0) { for (i=2; i<n; ++i) f[q][i][e[i-2]] = d[1][i]; } else { for (i=2; i<n; ++i) f[q][i][e[i-2]] = d[n][i]; } //dp for (j=1; j<e[n-2]; ++j) if (cnt[j] < n2) for (i=2; i<n; ++i) if (f[q][i][j] < inf) for (k=2; k<n; ++k) if (f[q][i][j]+d[i][k] < f[q][k][j|e[k-2]]) f[q][k][j|e[k-2]] = f[q][i][j]+d[i][k]; } ans = inf; //枚举先走到的一半为sta for (sta=0; sta<e[n-2]; ++sta) if (cnt[sta] == n1) { //前半段 x = inf; //x记录前半段的最短距离 //枚举前一半中最后一个收割的点是i for (i=2; i<n; ++i) if (sta&e[i-2]) //枚举后一半中第一个收割的点是j for (j=2; j<n; ++j) if (!(sta&e[j-2])) if (f[0][i][sta]+d[i][j]+f[1][j][e[n-2]-1-sta] < x) x = f[0][i][sta]+d[i][j]+f[1][j][e[n-2]-1-sta]; //后半段 //枚举前一半中最后一个播种的点是i for (i=2; i<n; ++i) if (sta&e[i-2]) //枚举后一半中第一个播种的点是j for (j=2; j<n; ++j) if (!(sta&e[j-2])) if (x+f[1][i][sta]+d[i][j]+f[0][j][e[n-2]-1-sta] < ans) ans = x+f[1][i][sta]+d[i][j]+f[0][j][e[n-2]-1-sta]; } printf("%d\n", ans); return 0; }
标签:进制 动态 哪些 sizeof inline city 2.0 while algo
原文地址:http://www.cnblogs.com/lyqlyq/p/7780370.html