Logistic Regression-Cost Fuction

标签：rac   ict   ram   div   other   class   cti   csu   全局最优   

1. 二分类问题

• 样本：  ，训练样本包含  个；
• 其中  ，表示样本 包含 个特征；
•  ，目标值属于0、1分类；
• 训练数据： 

输入神经网络时样本数据的形状：

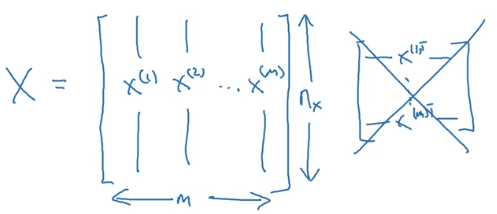
目标数据的形状： 

2. logistic Regression

逻辑回归中，预测值： 

其表示为1的概率，取值范围在  之间。 引入Sigmoid函数，预测值： 

其中

注意点：函数的一阶导数可以用其自身表示， 

这里可以解释梯度消失的问题，当  时，导数最大，但是导数最大为  ，这里导数仅为原函数值的0.25倍。 参数梯度下降公式的不断更新，  会变得越来越小，每次迭代参数更新的步伐越来越小，最终接近于0，产生梯度消失的现象。

3. logistic回归 损失函数

Loss function

一般经验来说，使用平方错误（squared error）来衡量Loss Function： 

但是，对于logistic regression 来说，一般不适用平方错误来作为Loss Function，这是因为上面的平方错误损失函数一般是非凸函数（non-convex），其在使用低度下降算法的时候，容易得到局部最优解，而不是全局最优解。因此要选择凸函数。 

逻辑回归的Loss Function： 

• 当  时，  。如果  越接近1，  ，表示预测效果越好；如果  越接近0，  ，表示预测效果越差； 
• 当  时，  。如果  越接近0，  ，表示预测效果越好；如果  越接近1，  ，表示预测效果越差； 
• 我们的目标是最小化样本点的损失Loss Function，损失函数是针对单个样本点的。

Cost function

全部训练数据集的Loss function总和的平均值即为训练集的代价函数（Cost function）。

• Cost function是待求系数w和b的函数；
• 我们的目标就是迭代计算出最佳的w和b的值，最小化Cost function，让其尽可能地接近于0。

################################################################################################################################################

注意：

1）定义cost function的目的是为了训练logistic 回归模型的参数 w 和 b

loss fuction 是在单个训练样本上定义的，而cost fuction 是在全体训练样本上定义的

Logistic Regression-Cost Fuction

标签：rac   ict   ram   div   other   class   cti   csu   全局最优   

原文地址：http://www.cnblogs.com/Bella2017/p/7780586.html