标签:实现 子矩阵 rand 治法 就是 multi com matlab 代码
在公茂果老师的课件中,给出了三种矩阵相乘的方法:
1. 利用矩阵定义,对矩阵进行运算。即C(i,j)=A(i,k)*B(k,j),时间复杂度为:
其实现代码为:
tic;
C2=zeros(n(m));
for i=1:n(m)
for j=1:n(m)
for k=1:n(m)
C2(i,j)=C2(i,j)+A(i,k)*B(k,j);
end
end
end
t2(m)=toc;
2.利用分治法进行计算。分治法的核心,在于将原问题切割,这里将原矩阵A与B,分别切割成四个子矩阵,分别得到C11,C12,C21,C22,在矩阵相乘阶段,利用的是MATLAB自带的矩阵相乘函数。
对于C11为例,其时间复杂度为:
期实代码为
A11=A(1:n(m)/2,1:n(m)/2);
A12=A(1:n(m)/2,n(m)/2+1:n(m));
A21=A(n(m)/2+1:n(m),1:n(m)/2);
A22=A(n(m)/2+1:n(m),n(m)/2+1:n(m));
B11=B(1:n(m)/2,1:n(m)/2);
B12=B(1:n(m)/2,n(m)/2+1:n(m));
B21=B(n(m)/2+1:n(m),1:n(m)/2);
B22=B(n(m)/2+1:n(m),n(m)/2+1:n(m));
%矩阵计算,开始计时
tic;
C3=zeros(n(m));
C11=A11*B11+A12*B21;
C12=A11*B12+A12*B22;
C21=A21*B11+A22*B21;
C22=A21*B12+A22*B22;
C3=[C11 C12;C21 C22];
t3(m)=toc;
3.利用Strassen方法

上面的图片,已经给的非常的清楚,其时间复杂度为n2.81
下面贴出完整的代码
clc;
close all;
clear all;
n=[2^2 2^3 2^4 2^5 2^6 2^7 2^8 2^9 2^10 2^11 2^12];
for m=1:11
%%%%采用MATLAB自带函数进行矩阵相乘
A=round(rand(n(m)));%生成随机矩阵A
B=round(rand(n(m)));%生成随机矩阵B
%自带函数计时
tic;
C1=A*B;
t1(m)=toc;
%按照矩阵相乘的定义进行计算
tic;
C2=zeros(n(m));
for i=1:n(m)
for j=1:n(m)
for k=1:n(m)
C2(i,j)=C2(i,j)+A(i,k)*B(k,j);
end
end
end
t2(m)=toc;
%分治法,思路,对AB矩阵进行切割后,仍使用MATLAB自带的函数进行
%步骤一,将原来的矩阵分块切割成四个,这四个子矩阵,还会用到Strassen的方法中
A11=A(1:n(m)/2,1:n(m)/2);
A12=A(1:n(m)/2,n(m)/2+1:n(m));
A21=A(n(m)/2+1:n(m),1:n(m)/2);
A22=A(n(m)/2+1:n(m),n(m)/2+1:n(m));
B11=B(1:n(m)/2,1:n(m)/2);
B12=B(1:n(m)/2,n(m)/2+1:n(m));
B21=B(n(m)/2+1:n(m),1:n(m)/2);
B22=B(n(m)/2+1:n(m),n(m)/2+1:n(m));
%矩阵计算,开始计时
tic;
C3=zeros(n(m));
C11=A11*B11+A12*B21;
C12=A11*B12+A12*B22;
C21=A21*B11+A22*B21;
C22=A21*B12+A22*B22;
C3=[C11 C12;C21 C22];
t3(m)=toc;
%Strassen方法,公茂果老师的课件中,已经给出了初始化方法
tic;
C4=zeros(n(m));
M1=A11*(B12-B22);
M2=(A11+A12)*B22;
M3=(A21+A22)*B11;
M4=A22*(B21-B11);
M5=(A11+A22)*(B11+B22);
M6=(A12-A22)*(B21+B22);
M7=(A11-A21)*(B11+B12);
C11=M5+M4-M2+M6;
C12=M1+M2;
C21=M3+M4;
C22=M5+M1-M3-M7;
C4=[C11 C12;C21 C22];
t4(m)=toc;
end
%这里四个方法已经全部结束,接下来就是输出图片
x=log(n)/log(2)%横轴取对数
plot(x,t1,x,t2,x,t3,x,t4);
xlabel(‘log(n)/log(2)‘);
ylabel(‘time‘);
title(‘The comparison chart of four different methods for Matrix multiplication‘)
运行时间比较长,请耐心等待。其结果为:
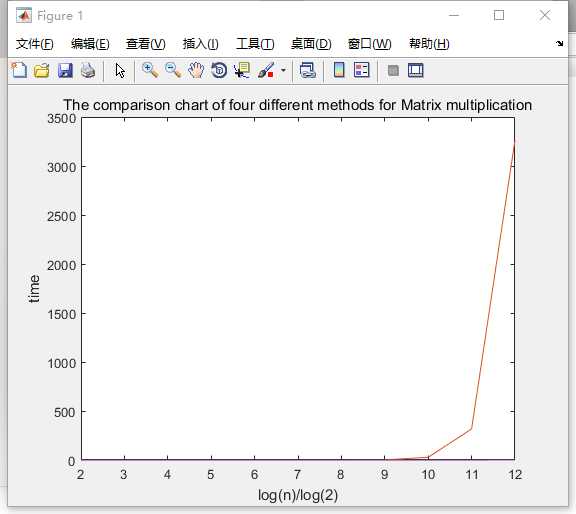
没设置好,所以,看着不是特别清楚,可以在关键的节点处,设置*等,特别现实一下。
标签:实现 子矩阵 rand 治法 就是 multi com matlab 代码
原文地址:http://www.cnblogs.com/jtailong/p/7783023.html