标签:替换 创建 文件夹 arch 后序 roo logs for 遍历
一、二叉树的基本概念
一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。如下图:
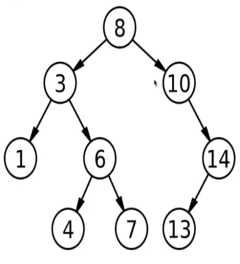
数字8为根节点,1、4、7、13为叶子节点,8的左边为左子树,数值都比根节点8小,右边为右子树,数值都比根节点8大。
二、二叉树的遍历
前序遍历:根->左->右(8-3-1-6-4-7-10-14-13);
中序遍历:左->根->右(1-3-4-6-7-8-10-13-14);
后序遍历:左->右->根(1-4-7-6-3-13-14-10-8);
典型应用分析:
1) 输出某个文件夹下所有文件名称(可以有子文件夹)---用先序遍历实现:
如果是文件夹,先输出文件夹名,然后再依次输出该文件夹下的所有文件(包括子文件夹),如果有子文件夹,则再进入该子文件夹,输出该子文件夹下的所有文件名。
2) 统计某个文件夹的大小(该文件夹下所有文件的大小--用后序遍历实现:
若要知道某文件夹的大小,必须先知道该文件夹下所有文件的大小,如果有子文件夹,若要知道该子文件夹大小,必须先知道子文件夹所有文件的大小。
3)从小到大输出数据---中序遍历实现
三、创建二叉树的实现(递归算法)
//创建二叉树
var BinaryTree=function(){
var Node=function(key){//初始化节点
this.key=key;
this.left=null;
this.right=null;
}
var rootNode=null;
var insertNode=function(node,newNode){
//插入的节点与父节点比较,小的在左边,大的在右边
if(newNode.key< node.key){
if(node.left ===null){
node.left=newNode;
}else{
insertNode(node.left,newNode);
}
}else{
if(node.right===null){
node.right=newNode;
}else{
insertNode(node.right,newNode);
}
}
}
this.insert=function(key){
var newNode=new Node(key);
if(rootNode===null){
rootNode=newNode;
}else{
insertNode(rootNode,newNode);
}
}
}
var nodes=[8,3,10,1,6,14,4,7,13];
var binaryTree=new BinaryTree();
nodes.forEach(function(key){
binaryTree.insert(key);
});
四、三种遍历的实现
//中序遍历
var inOrderTraverseNode=function(node,callback){
if(node !==null){
inOrderTraverseNode(node.left,callback);
callback(node.key);
inOrderTraverseNode(node.right,callback);
}
}
this.inOrderTraverse=function(callback){
inOrderTraverseNode(rootNode,callback);
};
//前序遍历
var preOrderTraverseNode=function(node,callback){
if(node !==null){
callback(node.key);
preOrderTraverseNode(node.left,callback);
preOrderTraverseNode(node.right,callback);
}
}
this.preOrderTraverse=function(callback){
preOrderTraverseNode(rootNode,callback);
};
//后序遍历
var afterOrderTraverseNode=function(node,callback){
if(node !==null){
afterOrderTraverseNode(node.left,callback);
afterOrderTraverseNode(node.right,callback);
callback(node.key);
}
}
this.afterOrderTraverse=function(callback){
afterOrderTraverseNode(rootNode,callback);
};
//以上代码放在BinaryTree函数里面定义
var callback=function(key){
console.log(key);
}
binaryTree.preOrderTraverse(callback);
五、二叉树节点查找
最小值:由于左节点总是比右节点大,所以只要判断该节点没有左节点就是最大值。
最大值:只要判断该节点没有右节点就是最大值。
指定值:运用递归方法进行比较,小于父节点就走左子树,大于就走右子树,直到等于指定值。代码如下:
var minNode=function(node){
if(node){
while(node && node.left !==null){
node=node.left;
}
return node.key;
}
return null;
}
this.min=function(){
return minNode(rootNode);
}
var maxNode=function(node){
if(node){
while(node && node.right !==null){
node=node.right;
}
return node.key;
}
return null;
}
this.max=function(){
return maxNode(rootNode);
}
var searchNode=function(node,key){
if(node===null){
return false;
}
if(key<node.key){
return searchNode(node.left,key);
}else if(key>node.key){
return searchNode(node.right,key);
}else{
return true;
}
}
this.search=function(key){
return searchNode(rootNode,key)
}
//以上代码放在BinaryTree函数里面定义;
console.log(binaryTree.min())//查找最小值
console.log(binaryTree.search(7)?‘has‘:‘no found 7‘)//查找指定值7
六、删除节点
1、删除叶子节点
通过递归方法,如果节点没有左节点和右节点就是叶子节点,通过node =null删除该节点。
2、删除只有左子树或者右子树的节点,比如删除节点10,那原先指向10的箭头就指向14.
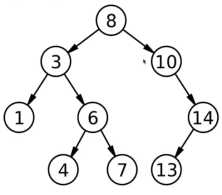
3、删除左子树右子树都有的节点,比如节点3。由于左节点一定比父节点和右节点大,所以删除节点3后,节点4将代替节点3的位置,节点4和连接的箭头消失。如下图:
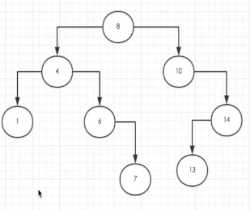
4、代码实现如下:
var findMinNode=function(node){
if(node){
while(node && node.left !==null){
node=node.left;
}
return node;
}
return null;
}
var removeNode=function(node,key){
if(node===null){
return null;
}
if(key<node.key){
node.left=removeNode(node.left,key);
return node;
}else if(key>node.key){
node.right=removeNode(node.right,key);
return node;
}else{
//删除左右节点都没有的节点
if(node.left===null && node.right===null){
node=null;
return node;
}else if(node.left===null){//删除左节点没有的节点
node=node.right;
return node;
}else if(node.right===null){//删除右节点没有的节点
node=node.left;
return node;
}
//删除左右节点都有的节点
var aux=findMinNode(node.right);//查找该节点右子树最小值
node.key=aux.key;//替换要删除的节点
//删除掉要删除节点的右子树的最小值,也就是aux;
node.right=removeNode(node.right,aux.key);
return node;
}
}
this.remove=function(key){
rootNode=removeNode(rootNode,key)
}
以上代码放在BinaryTree这个函数里面定义。
binaryTree.remove(3);
这里的代码实现主要用的是递归方法,大家可以在浏览器上打断点执行理解。
标签:替换 创建 文件夹 arch 后序 roo logs for 遍历
原文地址:http://www.cnblogs.com/wangdan0915/p/7791785.html