标签:2-2 解决 探讨 就是 分割 img 技术分享 重要 区间
积分,简而言之,可以分为不定积分与定积分,不定积分只是导数的逆运算,而定积分是求一个函数的图形在一个闭区间上和x坐标轴围成的面积,定积分的正式名称是黎曼积分,用黎曼自己的话来说,就是把直角坐标系上的函数的图象用平行于y轴的直线把其分割成无数个矩形,然后把某个区间[a,b]上的矩形累加起来,所得到的就是这个函数的图象在区间[a,b]的面积,实际上,定积分的上下限就是区间的两个端点a,b,在一定条件之下,函数f(x)在闭区间[a, b]上的定积分(黎曼积分)为:
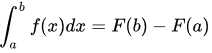
我将不定积分与定积分(黎曼积分)都叫作一般积分,黎曼积分的核心思想就是试图通过无限逼近来确定这个积分值,我们称这个积分值为黎曼和,但是,黎曼积分也有一些不可积的问题,例如:狄利克雷函数,狄拉克δ函数.
狄利克雷函数
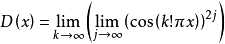
狄拉克δ函数
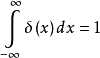
这时,我们就要推广黎曼积分,以求能解决一些不可积的问题.
我们知道,黎曼积分他是面积的推广,在相当广泛的场合,他也够用了,但是,随着人们对客观世界的不断深化,特别是在18世纪,有关热,波,电磁等的研究需要,数学上必须对函数项级数,含参变量的函数等进行更深入的探讨,若导数是质点运动的速度,加速度的表达,那积分就是表达功,能量的重要思想,随着物理学的发展,迫切需要一个比黎曼积分更有效的积分,他既保持黎曼积分的直观性,又能在逐项积分方面比黎曼积分所需的条件有较大的改进,于是,勒贝格积分产生了.
黎曼积分与勒贝格积分之差异
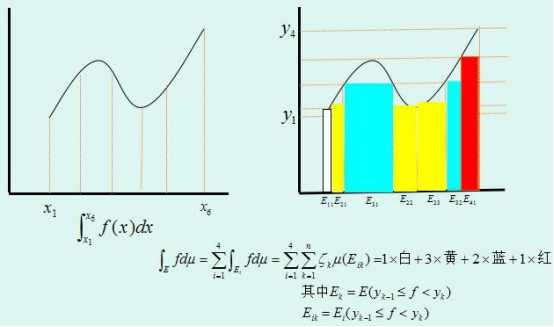
标签:2-2 解决 探讨 就是 分割 img 技术分享 重要 区间
原文地址:http://www.cnblogs.com/milantgh/p/7794054.html