题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入输出格式
输入格式:
第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式:
一行,包含一个正整数,即为该网络的最大流。
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
样例说明:
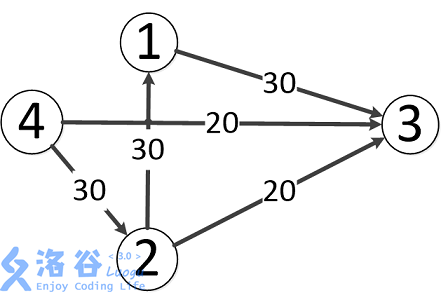
题目中存在3条路径:
4-->2-->3,该路线可通过20的流量
4-->3,可通过20的流量
4-->2-->1-->3,可通过10的流量(边4-->2之前已经耗费了20的流量)
故流量总计20+20+10=50。输出50。
#include<queue> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define NAXN 10001 #define MAXN 100001 using namespace std; int n,m,s,t; int tot=1,ans; int cur[NAXN],lev[NAXN]; int to[MAXN*2],net[MAXN*2],cap[MAXN*2],head[NAXN]; void add(int u,int v,int w){ to[++tot]=v;cap[tot]=w;net[tot]=head[u];head[u]=tot; to[++tot]=u;cap[tot]=0;net[tot]=head[v];head[v]=tot; } bool bfs(){ queue<int>que; for(int i=1;i<=n;i++){ lev[i]=-1; cur[i]=head[i]; } lev[s]=0; que.push(s); while(!que.empty()){ int now=que.front(); que.pop(); for(int i=head[now];i;i=net[i]) if(lev[to[i]]==-1&&cap[i]>0){ lev[to[i]]=lev[now]+1; que.push(to[i]); if(to[i]==t) return true; } } return false; } int dinic(int now,int flow){ if(now==t) return flow; int rest=0,detal; for(int & i=cur[now];i;i=net[i]) if(cap[i]>0&&lev[to[i]]==lev[now]+1){ detal=dinic(to[i],min(flow-rest,cap[i])); if(detal){ rest+=detal; cap[i]-=detal; cap[i^1]+=detal; if(rest==flow) break; } } if(rest!=flow) lev[now]=-1; return rest; } int main(){ cin>>n>>m>>s>>t; for(int i=1;i<=m;i++){ int u,v,w; scanf("%d%d%d",&u,&v,&w); add(u,v,w); } while(bfs()) ans+=dinic(s,0x7fffffff); cout<<ans; }
