标签:span set 测试的 优化 .com vector find 防止 str
引用请注明出处:http://www.cnblogs.com/lihaiping/p/7799495.html
最近项目开发中遇到一个和找零钱很相似的问题,所以网上搜索了一下,大部分的问题,都是关于如何求出找零钱的方法数(有多少种找零的方法)和如何求少找零的方案。
但我这次的问题,需要在求出找零钱方法数的同时还需要求出这些方法中的每种具体找零方法。
根据网上的代码,求找零方法数种类:(动态规划的算法)
1 int countWays(vector<int> changes, int n, int x) { 2 // 待兑换的金额是i,可用的范围是0-j-1 3 // i = x,j = 0-n-1 4 //int dp[x+1][n]; 5 6 //使用动态开辟二维数组 7 int **dp = new int*[x+1]; 8 for(int i=0;i<(x+1);i++) 9 { 10 dp[i] = new int[n]; 11 memset(dp[i],0,n*sizeof(int)); 12 } 13 // 当待兑换的金额是0的时候,都是只有一种,就是空集 14 for(int i=0;i<n;i++){// 15 dp[0][i] = 1; 16 } 17 18 // 第1列,待兑换的钱是i,因为只能用第一种零钱,所以只有当是第一种零钱的整数倍的时候,才有一种兑换方法 19 for (int i = 1; i <= x; i++) { 20 if (i % changes[0] == 0) { 21 dp[i][0] = 1; 22 } 23 } 24 for (int i = 1; i <= x; i++) 25 { 26 for (int j = 1; j < n; j++) 27 { 28 if (i - changes[j] >= 0) 29 { 30 dp[i][j] += (dp[i][j-1] + dp[i - changes[j]][j]); 31 } 32 else{ 33 dp[i][j] += dp[i][j-1]; 34 } 35 } 36 } 37 int count=dp[x][n-1]; 38 39 40 for(int k=0;k<(x+1);k++) 41 delete []dp[k]; 42 43 delete []dp; 44 45 return count; 46 }
下面为我改造求找零方法数的同时并记录下找零的具体方法:
1 //map<待兑换金额,map<所用找零的面值,找零具体方案vector<vector<int> > >> 2 map<int,map<int,vector<vector<int> > > > mapAimChanges; 3 4 int countWaysEx(vector<int> changes, int n, int x) { 5 // 待兑换的金额是i,可用的范围是0-j-1 6 // i = x,j = 0-n-1 7 //int dp[x+1][n]; 8 9 //使用动态开辟二维数组 10 int **dp = new int*[x+1]; 11 for(int i=0;i<(x+1);i++) 12 { 13 dp[i] = new int[n]; 14 memset(dp[i],0,n*sizeof(int)); 15 } 16 17 18 19 // 当待兑换的金额是0的时候,都是只有一种,就是空集 20 for(int i=0;i<n;i++){// 21 dp[0][i] = 1; 22 } 23 //mapAimChanges.insert(pair<int,map<int,vector<vector<int> > > >(0,mapVecVecTemp_0)); 24 25 // 第1列,待兑换的钱是i,因为只能用第一种零钱,所以只有当是第一种零钱的整数倍的时候,才有一种兑换方法 26 for (int i = 1; i <= x; i++) { 27 if (i % changes[0] == 0) { 28 //一维数组,具体找零方案 29 vector<int> vecTemp(i/changes[0],changes[0]); 30 //找零方案的组合,形成一个二维数组 31 vector<vector<int> > vecvecTemp(1,vecTemp); 32 //存储所用零钱 33 map<int,vector<vector<int> > > mapVecVecTemp; 34 mapVecVecTemp.insert(pair<int,vector<vector<int> > >(0,vecvecTemp)); 35 36 mapAimChanges.insert(pair<int,map<int,vector<vector<int> > > >(i,mapVecVecTemp)); 37 38 dp[i][0] = 1; 39 } 40 } 41 for (int i = 1; i <= x; i++) 42 { 43 for (int j = 1; j < n; j++) 44 { 45 if (i - changes[j] >= 0) 46 { 47 //找零方案的组合,二维数组 48 vector<vector<int> > vecvecTempGoup; 49 //存储所用零钱索引j的找零方案组合 50 map<int,vector<vector<int> > > mapVecVecTemp; 51 52 map<int,map<int,vector<vector<int> > > >::iterator iter1=mapAimChanges.find(i); 53 if (iter1!=mapAimChanges.end()) 54 { 55 mapVecVecTemp=iter1->second;//进行一次拷贝,防止后续在earse的时候出现其他内容的丢失 56 //查找上一个索引j-1 57 map<int,vector<vector<int> > >::iterator iter2=iter1->second.find(j-1); 58 if (iter2!=iter1->second.end()) 59 {//如果找到 60 //先把j-1的内容拷贝 61 vecvecTempGoup=iter2->second; 62 } 63 } 64 65 //添加新的方案 66 vector<vector<int> > vecvecTemp2;//新的找零二维数组方案 67 iter1=mapAimChanges.find(i - changes[j]);//查找之前对i-change[j]的找零方案 68 if (iter1!=mapAimChanges.end()) 69 { 70 //查找上一个索引j 71 map<int,vector<vector<int> > >::iterator iter2=iter1->second.find(j); 72 if (iter2!=iter1->second.end()) 73 {//如果找到 74 //对于i-changes[j]的零钱在j这个索引上所用的所有找零方案, 75 //我们需要在之前的基础上插入一个新的元素changes[i],形成一个新的找零方案 76 vector<vector<int> > vecvecTemp; 77 vecvecTemp=iter2->second; 78 79 vector<vector<int> >::iterator vecvecIter3=vecvecTemp.begin(); 80 for (;vecvecIter3!=vecvecTemp.end();vecvecIter3++) 81 { 82 vector<int> vecTemp=*vecvecIter3; 83 vecTemp.push_back(changes[j]); 84 //将生成的新找零方案,放入二维数组 85 vecvecTemp2.push_back(vecTemp); 86 } 87 } 88 } 89 else//说明找到的是为空集 90 {//说明i - changes[j]==0,才会为空集 91 vector<int> vecTemp_0(1,changes[j]); 92 vecvecTemp2.push_back(vecTemp_0); 93 } 94 95 if (!vecvecTemp2.empty()) 96 { 97 vecvecTempGoup.insert(vecvecTempGoup.end(),vecvecTemp2.begin(),vecvecTemp2.end()); 98 } 99 if (!vecvecTempGoup.empty()) 100 { 101 mapVecVecTemp.erase(j); 102 mapVecVecTemp.insert(pair<int,vector<vector<int> > >(j,vecvecTempGoup)); 103 mapAimChanges.erase(i); 104 mapAimChanges.insert(pair<int,map<int,vector<vector<int> > > >(i,mapVecVecTemp)); 105 } 106 107 108 dp[i][j] += (dp[i][j-1] + dp[i - changes[j]][j]); 109 } 110 else{ 111 //找零方案的组合,二维数组 112 vector<vector<int> > vecvecTemp; 113 map<int,map<int,vector<vector<int> > > >::iterator iter1=mapAimChanges.find(i); 114 if (iter1!=mapAimChanges.end()) 115 { 116 //存储所用零钱索引j的找零方案组合 117 map<int,vector<vector<int> > > mapVecVecTemp=iter1->second; 118 //查找上一个索引 119 map<int,vector<vector<int> > >::iterator iter2=iter1->second.find(j-1); 120 if (iter2!=iter1->second.end()) 121 {//如果找到 122 vecvecTemp=iter2->second; 123 mapVecVecTemp.insert(pair<int,vector<vector<int> > >(j,vecvecTemp)); 124 125 //map操作的时候,相同的key的时候,会出现insert失败,而不是覆盖 126 //所以这里需要先进行删除 127 mapAimChanges.erase(i); 128 //mapAimChanges.erase(iter1); 129 mapAimChanges.insert(pair<int,map<int,vector<vector<int> > > >(i,mapVecVecTemp)); 130 } 131 } 132 dp[i][j] += dp[i][j-1]; 133 } 134 } 135 } 136 int count=dp[x][n-1]; 137 138 139 for(int k=0;k<(x+1);k++) 140 delete []dp[k]; 141 142 delete []dp; 143 144 return count; 145 }
下面为测试的代码:
1 vector<int> vecRmb; 2 vecRmb.push_back(1); 3 vecRmb.push_back(2); 4 vecRmb.push_back(3); 5 6 int ret=countWays(vecRmb,vecRmb.size(),5); 7 printf("ret=%d\n",ret); 8 9 ret=countWaysEx(vecRmb,vecRmb.size(),5); 10 printf("ret=%d\n",ret); 11 map<int,map<int,vector<vector<int> > > >::iterator map_iter=mapAimChanges.find(5); 12 if (map_iter!=mapAimChanges.end()) 13 { 14 map<int,vector<vector<int> > >::iterator map_iter2=map_iter->second.find(vecRmb.size()-1); 15 if (map_iter2!=map_iter->second.end()) 16 { 17 vector<vector<int> >::iterator vec_vec_iter3=map_iter2->second.begin(); 18 printf("size:%d\n",map_iter2->second.size()); 19 for (;vec_vec_iter3!=map_iter2->second.end();vec_vec_iter3++) 20 { 21 vector<int> vecTemp=*vec_vec_iter3; 22 for (int i=0;i<vecTemp.size();i++) 23 { 24 printf("["); 25 printf(" %d ",vecTemp.at(i)); 26 printf("]"); 27 } 28 printf("\n"); 29 } 30 } 31 32 }
打印结果:
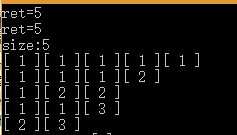
其中方法和数据结构没有进行优化,如果有优化的方法,各位可以提出来,我们一起改造这个经典问题。
标签:span set 测试的 优化 .com vector find 防止 str
原文地址:http://www.cnblogs.com/lihaiping/p/7799495.html