吴恩达 DeepLearning.ai课程笔记（1-3）神经网络和深度学习 --- 浅层神经网络

标签：random   code   --   过程   范围   项目   original   二分   梯度下降算法   

以下为在Coursera上吴恩达老师的DeepLearning.ai课程项目中，第一部分《神经网络和深度学习》第二周课程部分关键点的笔记。笔记并不包含全部小视频课程的记录，如需学习笔记中舍弃的内容请至 Coursera 或者 网易云课堂。同时在阅读以下笔记之前，强烈建议先学习吴恩达老师的视频课程。

1. 二分类问题

对于二分类问题，大牛给出了一个小的Notation。

• 样本：  ，训练样本包含  个；
• 其中  ，表示样本 包含 个特征；
•  ，目标值属于0、1分类；
• 训练数据： 

输入神经网络时样本数据的形状：

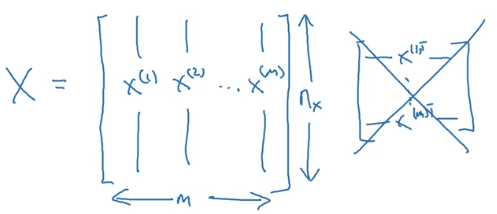
目标数据的形状：

2. logistic Regression

逻辑回归中，预测值：

其表示为1的概率，取值范围在  之间。 引入Sigmoid函数，预测值：

其中

注意点：函数的一阶导数可以用其自身表示，

这里可以解释梯度消失的问题，当  时，导数最大，但是导数最大为  ，这里导数仅为原函数值的0.25倍。 参数梯度下降公式的不断更新，  会变得越来越小，每次迭代参数更新的步伐越来越小，最终接近于0，产生梯度消失的现象。

3. logistic回归 损失函数

Loss function

一般经验来说，使用平方错误（squared error）来衡量Loss Function：

但是，对于logistic regression 来说，一般不适用平方错误来作为Loss Function，这是因为上面的平方错误损失函数一般是非凸函数（non-convex），其在使用低度下降算法的时候，容易得到局部最优解，而不是全局最优解。因此要选择凸函数。

逻辑回归的Loss Function：

• 当  时，  。如果  越接近1，  ，表示预测效果越好；如果  越接近0，  ，表示预测效果越差；
• 当  时，  。如果  越接近0，  ，表示预测效果越好；如果  越接近1，  ，表示预测效果越差；
• 我们的目标是最小化样本点的损失Loss Function，损失函数是针对单个样本点的。

Cost function

全部训练数据集的Loss function总和的平均值即为训练集的代价函数（Cost function）。

• Cost function是待求系数w和b的函数；
• 我们的目标就是迭代计算出最佳的w和b的值，最小化Cost function，让其尽可能地接近于0。

4. 梯度下降

用梯度下降法（Gradient Descent）算法来最小化Cost function，以计算出合适的w和b的值。

每次迭代更新的修正表达式：

在程序代码中，我们通常使用dw来表示  ，用db来表示  。

5. 逻辑回归中的梯度下降法

对单个样本而言，逻辑回归Loss function表达式：

反向传播过程：

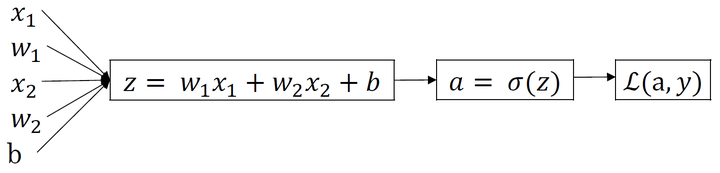
前面过程的da、dz求导：

再对  和b进行求导：

梯度下降法：

6. m个样本的梯度下降

对m个样本来说，其Cost function表达式如下：

Cost function 关于w和b的偏导数可以写成所有样本点偏导数和的平均形式：

7. 向量化（Vectorization）

在深度学习的算法中，我们通常拥有大量的数据，在程序的编写过程中，应该尽最大可能的少使用loop循环语句，利用python可以实现矩阵运算，进而来提高程序的运行速度，避免for循环的使用。

逻辑回归向量化

• 输入矩阵X：
• 权重矩阵w： 
• 偏置b：为一个常数
• 输出矩阵Y： 

所有m个样本的线性输出Z可以用矩阵表示：

python代码：

db = 1/m*np.sum(dZ)

单次迭代梯度下降算法流程

Z = np.dot(w.T,X) + b
A = sigmoid(Z)
dZ = A-Y
dw = 1/m*np.dot(X,dZ.T)
db = 1/m*np.sum(dZ)

w = w - alpha*dw
b = b - alpha*db

8. python的notation

虽然在Python有广播的机制，但是在Python程序中，为了保证矩阵运算的正确性，可以使用reshape()函数来对矩阵设定所需要进行计算的维度，这是个好的习惯；

如果用下列语句来定义一个向量，则这条语句生成的a的维度为（5，），既不是行向量也不是列向量，称为秩（rank）为1的array，如果对a进行转置，则会得到a本身，这在计算中会给我们带来一些问题。

a = np.random.randn(5)

如果需要定义（5，1）或者（1，5）向量，要使用下面标准的语句：

a = np.random.randn(5,1)
b = np.random.randn(1,5)

可以使用assert语句对向量或数组的维度进行判断。assert会对内嵌语句进行判断，即判断a的维度是不是（5，1），如果不是，则程序在此处停止。使用assert语句也是一种很好的习惯，能够帮助我们及时检查、发现语句是否正确。

assert(a.shape == (5,1))

可以使用reshape函数对数组设定所需的维度

a.reshape((5,1))

8. logistic regression代价函数的解释

Cost function的由来

预测输出  的表达式：

其中，  。

 可以看作预测输出为正类（+1）的概率：

当  时，  ；当  时，  。

将两种情况整合到一个式子中，可得：

对上式进行log处理（这里是因为log函数是单调函数，不会改变原函数的单调性）：

概率  越大越好，即判断正确的概率越大越好。这里对上式加上负号，则转化成了单个样本的Loss function，我们期望其值越小越好：

m个训练样本

假设样本之间是独立同分布的，我们总是希望训练样本判断正确的概率越大越好，则有：

同样引入log函数，加负号，则可以得到Cost function：

吴恩达 DeepLearning.ai课程笔记（1-3）神经网络和深度学习 --- 浅层神经网络

标签：random   code   --   过程   范围   项目   original   二分   梯度下降算法   

原文地址：http://www.cnblogs.com/koushihao/p/7801104.html