标签:前缀 play for 因子 ret span click 情况下 bre
其实我更想把他类比于符号函数,定义域N+,值域{-1,0,1}
定义函数:
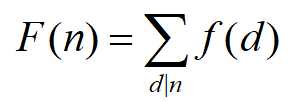
根据定义有:
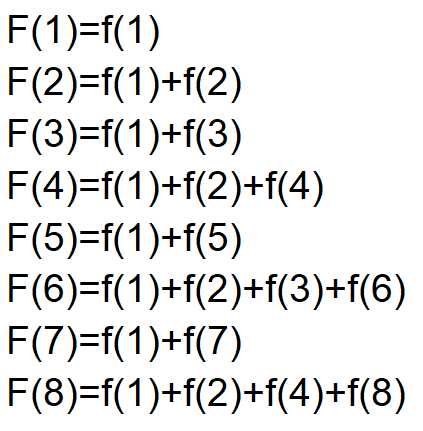
同时容易得出:

现定义公式:
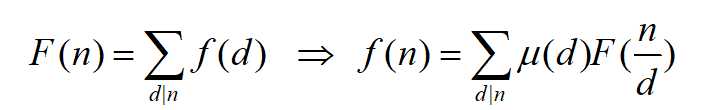
代入到上述f(i)的求取,我们可以得到:
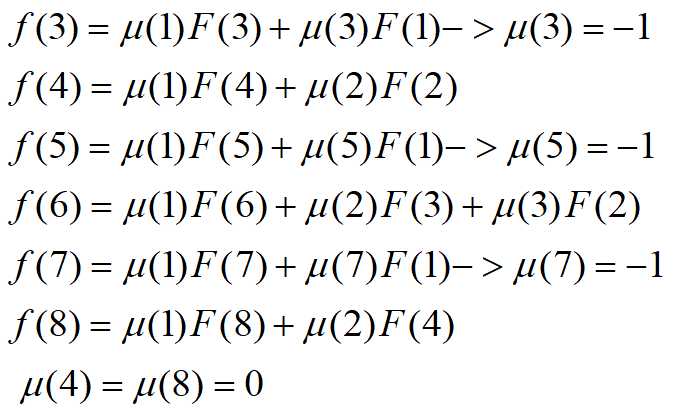
那么其中的μ(d)就是莫比乌斯函数,定义如下:
(1)当d=1时,μ(d)=1;
(2)当d=p1p2...pk为互异素数,μ(d)=-1;
(3)其他情况下,μ(d)=0.
莫比乌斯函数的性质:
(1)对于任意正整数有:
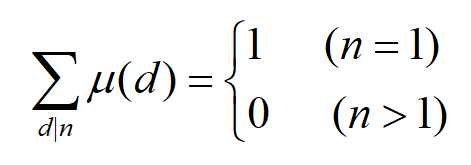
i:当n=1时,显然成立
ii:当n>1时,因为素因子存在,可以将n分解为:
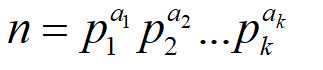
在r的所有因子中, 值不为零的只有所有质因子次数都为1的因子,其中质因数个数为r个的因子有Crk个
可以拿n=51450=2*3*5*5*7*7*7举例
其中质因数个数为1的因子有C17=7个。有:2 3 5 7 25 49 343
其他类比即可
那么有:
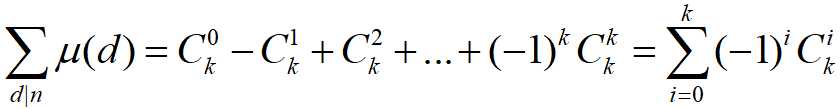
即证明:
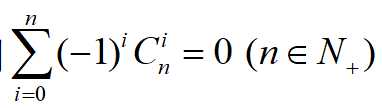
因为有二项式定理,将x=-1,y=-1,即证。
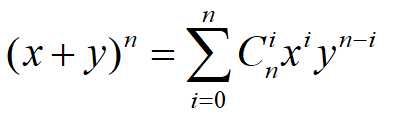
(2)莫比乌斯函数也是积性函数,所以其前缀和也是积性函数
两种求莫比乌斯函数的模板:
在线:

1 ll mubi(ll n) { 2 ll mu=1; 3 for(ll i=2;i*i<=n;++i) { 4 if(n%i==0) { 5 mu*=-1; 6 ll k=0; 7 do { 8 k++; 9 if(k>1) { 10 mu=0;break; 11 } 12 n/=i; 13 }while(n%i==0); 14 } 15 } 16 if(n>1) mu*=-1; 17 return mu; 18 }
离线:

1 mu[1]=1; 2 for(i=2;i<=n;i++) 3 { 4 if(!not_prime[i]) 5 { 6 prime[++tot]=i; 7 mu[i]=-1; 8 } 9 for(j=1;prime[j]*i<=n;j++) 10 { 11 not_prime[prime[j]*i]=1; 12 if(i%prime[j]==0) 13 { 14 mu[prime[j]*i]=0; 15 break; 16 } 17 mu[prime[j]*i]=-mu[i]; 18 } 19 }
标签:前缀 play for 因子 ret span click 情况下 bre
原文地址:http://www.cnblogs.com/lemonbiscuit/p/7801935.html