题目链接:http://115.28.76.232/problem?pid=1075
题意:定义一个f(n)函数,f(n) = a * f(n - 1) + b * f(n - 2), f(1) = c, f(2) = d.问f(n)在模1000000007情况下的最小循环节。即求最小的m,使对任意的n有f(n) % 1000000007 = f(n + m) % 1000000007.
思路:



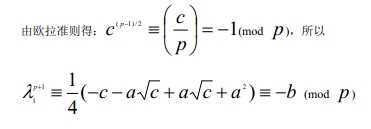


|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63 |
i64 p[] = {2, 3, 7, 109, 167, 500000003};i64 cnt[] = {4, 2, 1, 2, 1, 1 };i64 a,b,c,d;int judge(i64 x){ if(myPow(x,(mod-1)>>1,mod)==1) return
1; return
-1;}int
ok(i64 n){ Matrix A; A.init(0); A.a[0][0]=a; A.a[0][1]=b; A.a[1][0]=1; A.a[1][1]=0; A=A.Pow(n); i64 cc=(A.a[0][0]*c%mod+A.a[0][1]*d%mod)%mod; i64 dd=(A.a[1][0]*c%mod+A.a[1][1]*d%mod)%mod; return
cc==c&&dd==d;}i64 ans;void
DFS(i64 cur,int
dep){ if(dep==6) { if(ok(cur)&&(ans==-1||cur<ans)) ans=cur; return; } int
i; for(i=0;i<=cnt[dep];i++) { DFS(cur,dep+1); cur*=p[dep]; }}int
main(){ while(cin>>a>>b>>c>>d) { ans=-1; if(judge(a*a+4*b)==1) { if(ok(1)) ans=1; else
if(ok(2)) ans=2; else
if(ok(500000003)) ans=500000003; else
if(ok(mod-1)) ans=mod-1; } else { DFS(1,0); } printf("%lld\n",ans); }} |
acdream1075 神奇的%系列三(线代-矩阵-数论),布布扣,bubuko.com
原文地址:http://www.cnblogs.com/jianglangcaijin/p/3721017.html