线性判别分析（Linear Discriminant Analysis-LDA）

标签：目标   中心   es2017   方向   区分   限制   线性   width   .com   

Linear Discriminant Analysis(LDA线性判别分析)

　　用途：数据预处理中的降维，分类任务

　　目标：LDA关心的是能够最大化类间区分度的坐标轴成分，将特征空间（数据集中的多维样本）投影到一个维度更小的k维子空间中，同时保持区分类别的信息。

　　原理：投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近方法

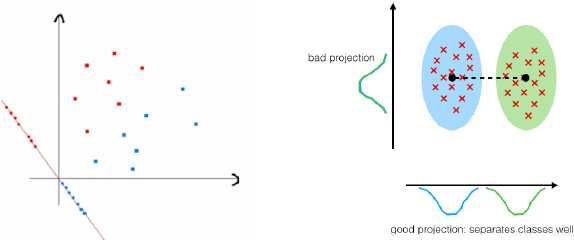
　　监督性：LDA是“有监督”的，它计算的是另一类特定的方向

　　投影：找到更合适分类的空间

　　与PCA不同，更关心分类而不是方差

数学原理

　　原始数据　　　　　　　　　　　　变换数据

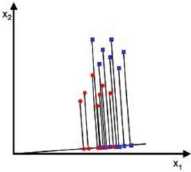
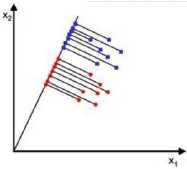
　　目标：找到该投影

　　LDA分类的一个目标是使得不同类别之间的距离越远越好，同一类别之中的距离越近越好

　　每类样例的均值

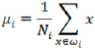
　　投影后的均值

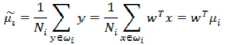
　　投影后的两类样本中心点尽量分离

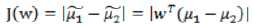
　　X1的方向可以最大化J(w)，但是却分的不好

　　散列值：样本点的密集程度，值越大，越分散，反之，越集中

　　同类之间应该越密集些：

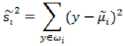
　　目标函数：

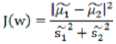
　　散列值公式展开：

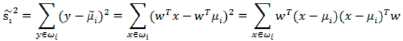
　　散列矩阵（scatter matrices）

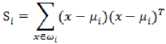
　　类内散步矩阵

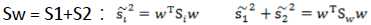
　　目标函数分子展开：

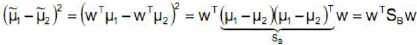
　　S_B称作类间散布矩阵

　　最终目标函数：

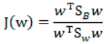
　　分母进行归一化：如果分子、分母是都可以取任意值的，那就会使得有无穷解，我们将分母限制为长度为1

　　拉格朗日乘子法：

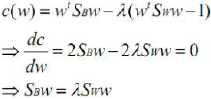
　　两边都乘以Sw的逆：

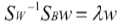
线性判别分析（Linear Discriminant Analysis-LDA）

标签：目标   中心   es2017   方向   区分   限制   线性   width   .com   

原文地址：http://www.cnblogs.com/hellojack/p/7804199.html