标签:移动 queue 问题 cond opp 100% 游戏 typedef eof
【问题描述】
小 B 最近迷上了华容道,可是他总是要花很长的时间才能完成一次。于是,他想到用编程来完成华容道:给定一种局面, 华容道是否根本就无法完成,如果能完成, 最少需要多少时间。
小 B 玩的华容道与经典的华容道游戏略有不同,游戏规则是这样的:
在一个 n*m 棋盘上有 n*m 个格子,其中有且只有一个格子是空白的,其余 n*m-1个格子上每个格子上有一个棋子,每个棋子的大小都是 1*1 的;
有些棋子是固定的,有些棋子则是可以移动的;
游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。
给定一个棋盘,游戏可以玩 q 次,当然,每次棋盘上固定的格子是不会变的, 但是棋盘上空白的格子的初始位置、 指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次
玩的时候, 空白的格子在第 EXi 行第 EYi 列,指定的可移动棋子的初始位置为第 SXi 行第 SYi列,目标位置为第 TXi 行第 TYi 列。
假设小 B 每秒钟能进行一次移动棋子的操作,而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间,或者告诉他不可能完成游戏。
输入格式:
输入文件为 puzzle.in。
第一行有 3 个整数,每两个整数之间用一个空格隔开,依次表示 n、m 和 q;
接下来的 n 行描述一个 n*m 的棋盘,每行有 m 个整数,每两个整数之间用一个空格隔开,每个整数描述棋盘上一个格子的状态,0 表示该格子上的棋子是固定的,1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行,每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi,每两个整数之间用一个空格隔开,表示每次游戏空白格子的位置,指定棋子的初始位置和目标位置。
输出格式:
输出文件名为 puzzle.out。
输出有 q 行,每行包含 1 个整数,表示每次游戏所需要的最少时间,如果某次游戏无法完成目标则输出−1。
【输入输出样例说明】
棋盘上划叉的格子是固定的,红色格子是目标位置,圆圈表示棋子,其中绿色圆圈表示目标棋子。
移动过程如下:
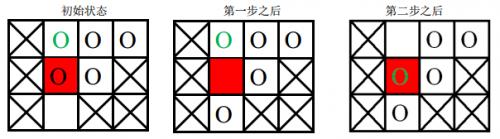
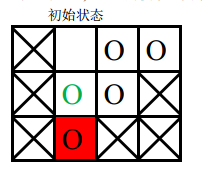
要将指定块移入目标位置,必须先将空白块移入目标位置,空白块要移动到目标位置,必然是从位置(2, 2)上与当前图中目标位置上的棋子交换位置,之后能与空白块交换位置的只有当前图中目标位置上的那个棋子,因此目标棋子永远无法走到它的目标位置, 游戏无法完成。
【数据范围】
对于 30%的数据,1 ≤ n, m ≤ 10,q = 1;
对于 60%的数据,1 ≤ n, m ≤ 30,q ≤ 10;
对于 100%的数据,1 ≤ n, m ≤ 30,q ≤ 500。
偶然发现快要联赛了历届的联赛题还没做完。。
感觉此题一看就有思路,毕竟n和m这么小,随便预处理
好吧我的算法其实和标算不大一样,
通过观察可以发现,空白块和目标棋子swap前后他们都是相邻的,所以只要处理处空白块从某个格子的相邻格子不经过该格,到达该格的另一个相邻格的最小代价,
最后每次SPFA一波,复杂度约为O(n ^ 4 + q * n ^ 2(玄学SPFA))。反正A了就是
#大括号不要换行!不要用tab缩进!运算符两边要空格!
#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
#define fi first
#define se second
#define mp make_pair
#define oppo(x) ((x + 2) & 3)
#define rep(i, x, y) for (int i = (x); i <= (y); i ++)
using namespace std;
typedef pair <int, int> pii;
const int N = 32;
const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int INF = 1e6;
struct node {
int x, y, p;
};
int cost[N][N][4][4], can[N][N];
int n, m, q;
int dis[N][N], vis[N][N], state = 0;
int Dis[N][N][4];
int inq[N][N][4];
inline int bfs(int sx, int sy, int ex, int ey, int bx = 0, int by = 0) {
if (!can[sx][sy] || !can[ex][ey]) return INF;
int f = can[bx][by];
can[bx][by] = 0;
state ++;
queue <pii> Q;
Q.push(mp(sx, sy));
vis[sx][sy] = state;
dis[sx][sy] = 0;
pii c; int x, y;
while (!Q.empty()) {
c = Q.front(); Q.pop();
if (c.fi == ex && c.se == ey) break;
x = c.fi; y = c.se;
rep(i, 0, 3)
if (can[x + dx[i]][y + dy[i]] && vis[x + dx[i]][y + dy[i]] != state) {
vis[x + dx[i]][y + dy[i]] = state;
dis[x + dx[i]][y + dy[i]] = dis[x][y] + 1;
Q.push(mp(x + dx[i], y + dy[i]));
}
}
if (vis[ex][ey] != state) dis[ex][ey] = INF;
can[bx][by] = f;
return dis[ex][ey];
}
inline void prework() {
int sx, sy, ex, ey;
rep(x, 1, n) rep(y, 1, m)
if (can[x][y])
rep(i, 0, 3) rep(j, i + 1, 3) {
sx = x + dx[i]; sy = y + dy[i];
ex = x + dx[j]; ey = y + dy[j];
cost[x][y][i][j] = cost[x][y][j][i] = bfs(sx, sy, ex, ey, x, y);
}
}
inline void solve() {
int sx, sy, ex, ey, tx, ty;
scanf("%d%d%d%d%d%d", &tx, &ty, &sx, &sy, &ex, &ey);
if (sx == ex && sy == ey) return (void) puts("0");
int d = bfs(sx, sy, ex, ey);
if (d == INF) return (void) puts("-1");
memset(Dis, 127, sizeof Dis);
queue <node> Q;
node c;
rep(i, 0, 3) {
d = bfs(tx, ty, sx + dx[i], sy + dy[i], sx, sy);
if (d != INF) {
Dis[sx + dx[i]][sy + dy[i]][oppo(i)] = d + 1;
Q.push((node){sx + dx[i], sy + dy[i], oppo(i)});
inq[sx + dx[i]][sy + dy[i]][oppo(i)] = 1;
}
}
int p, x, y;
while (!Q.empty()) {
c = Q.front(); Q.pop();
p = c.p; x = c.x; y = c.y;
inq[x][y][p] = 0;
rep(i, 0, 3)
if (i != p && cost[x][y][p][i] != INF && Dis[x + dx[i]][y + dy[i]][oppo(i)] > Dis[x][y][p] + cost[x][y][p][i] + 1) {
Dis[x + dx[i]][y + dy[i]][oppo(i)] = Dis[x][y][p] + cost[x][y][p][i] + 1;
if (!inq[x + dx[i]][y + dy[i]][oppo(i)]) {
inq[x + dx[i]][y + dy[i]][oppo(i)] = 1;
Q.push((node){x + dx[i], y + dy[i], oppo(i)});
}
}
}
int ans = INF;
rep(i, 0, 3) ans = min(ans, Dis[ex][ey][i]);
if (ans == INF) puts("-1");
else printf("%d\n", ans);
}
int main() {
scanf("%d%d%d", &n, &m, &q);
rep(i, 1, n)
rep(j, 1, m) scanf("%d", &can[i][j]);
prework();
while (q --) solve();
return 0;
}
标签:移动 queue 问题 cond opp 100% 游戏 typedef eof
原文地址:http://www.cnblogs.com/the-unbeatable/p/7805322.html