标签:相互 映射 .com 结果 component com ipa 最大 pca
Principal Component Analysis-PCA
用途:降维中最常用的一种手段
目标:提取最有价值的信息(基于方差)
内积:
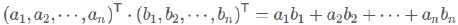
解释:
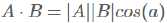
设向量B的模为1,则A与B的内积值等于A向B所在直线投影的矢量长度
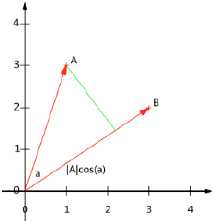
向量的表示及基变换
向量可以表示为(3,2)
实际上表示线性组合:
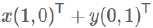
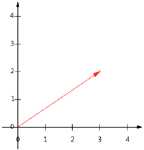
基:(1,0)和(0,1)叫做二位空间中的一组基
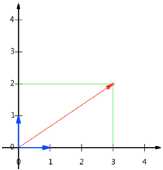
基变换
基是正交的(即内积为0,或直观说相互垂直)
要求:线性无关
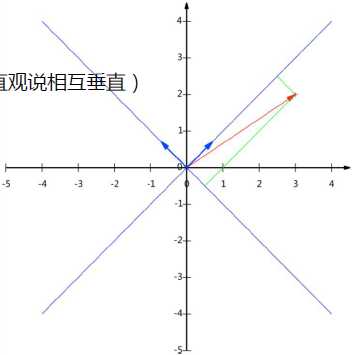
变换:数据与一个基做内积运算,结果作为第一个新的坐标分量,然后与第二个基做内积运算,结果作为第二个新坐标的分量
数据(3 , 2)映射到基中坐标:
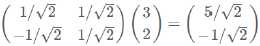
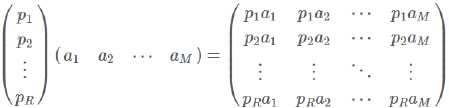
两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中的每一行行向量为基所表示的空间中去
协方差矩阵
方向:如何选择这个方向(或者说基)才能尽量保留最多的原始信息,希望投影后的投影值尽可能分散
方差:
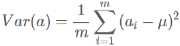
寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大
协方差(假设均值为0时):
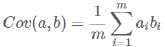
标签:相互 映射 .com 结果 component com ipa 最大 pca
原文地址:http://www.cnblogs.com/hellojack/p/7805048.html