标签:add target ref opened 乘法 iostream while matrix lld
哇!突然发现搜索‘模板’能搜到一坨。。。开始了默默刷模板的漫长之路。。。就让我最后在挣扎一下下吧!!!
待续。。。持续更新中。。。
好吧,不可相信这也是个模板。。

虽然说的那么。。那什么。。可是,真的不想自己弄唉(STL大法好)
①sort大法好!

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int n;
long long a[100010];
int main() {
scanf("%d",&n);
for(int i=0; i<n; i++) scanf("%lld",&a[i]);
sort(a,a+n);
for(int i=0; i<n; i++) printf("%lld ",a[i]);
return 0;
}
②真板子
——快速排序

#include <iostream>
#include <cstdio>
#include <algorithm>
#define mid ((l+r)>>1)
#define LL long long
using namespace std;
int n;
LL a[100010];
void Mysort(int l,int r) {
int i=l,j=r,m=a[mid];
while(i<=j) {
while(a[i]<m) i++;
while(a[j]>m) j--;
if(i<=j) {
LL tmp=a[i];
a[i]=a[j],a[j]=tmp;
i++,j--;
}
}
if(l<j) Mysort(l,j);
if(i<r) Mysort(i,r);
}
int main() {
scanf("%d",&n);
for(int i=0; i<n; i++) scanf("%lld",&a[i]);
Mysort(0,n-1);
for(int i=0; i<n; i++) printf("%lld ",a[i]);
return 0;
}
——归并排序

#include <iostream>
#include <cstdio>
#define LL long long
using namespace std;
const int M = 100010;
int n;
LL a[M],b[M];
void gsort(int l,int r) {
if(l==r) return;
int mid=l+r>>1;
gsort(l,mid),gsort(mid+1,r);
int i=l,j=mid+1,k=l;
while(i<=mid && j<=r) {
if(a[i]<=a[j]) b[k++]=a[i++];
else b[k++]=a[j++];
}
while(i<=mid) b[k++]=a[i++];
while(j<=r) b[k++]=a[j++];
for(int q=l; q<=r; q++) a[q]=b[q];
}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%lld",&a[i]);
gsort(1,n);
for(int i=1; i<=n; i++) printf("%lld ",a[i]);
return 0;
}
我以前原来没做过qaq,这样的板子题。。意会了好久233
我们可以以第一个串为标准,用第二个串来匹配第一个串,看能匹配多少。
所以,其实第一个串的每个数字其实影响不大,只有知道它对应了第二串的哪个数字就行,然后最后只要求一下上升序列就好辣~

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int M = 100010;
int n,len;
int a[M],b[M],belong[M];
int main() {
scanf("%d",&n);
//离散化一下
for(int i=1,x; i<=n; i++) {
scanf("%d",&x);
belong[x]=i;
}
for(int i=1,x; i<=n; i++) {
scanf("%d",&x);
a[i]=belong[x];
}
for(int i=1; i<=n; i++) { //find上升序列
if(a[i]>b[len]) {
b[++len]=a[i];
continue;
}
int k=lower_bound(b+1,b+1+len,a[i])-b;
b[k]=a[i];
}
printf("%d\n",len);
return 0;
}
今天刚学会qaq,考前的学新东西之一233
具体的嘛~我表示,只会背过+推矩阵

#include <iostream>
#include <cstdio>
typedef long long LL;
using namespace std;
inline LL readl() {
LL x=0,f=1; char c=getchar();
while(c<‘0‘ || c>‘9‘) { if(c==‘-‘) f=-1; c=getchar(); }
while(c>=‘0‘ && c<=‘9‘) x=x*10+c-‘0‘,c=getchar();
return x*f;
}
const int Mod = 1000000007;
LL n,m,i,j,k;
struct A {
LL a[105][105];
inline A operator * (const A &b) const {
A ret;
for(LL i=1; i<=n; i++)
for(LL j=1; j<=n; j++) {
ret.a[i][j]=0;
for(LL k=1; k<=n; k++)
ret.a[i][j]+=a[i][k]*b.a[k][j],
ret.a[i][j]%=Mod;
}
return ret;
}
}q;
A ksm(A a,LL x) {
A ret,k;
ret=a,k=a;
x--;
for(; x; x>>=1,k=k*k)
if(x&1) ret=ret*k;
return ret;
}
int main() {
n=readl();m=readl();
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
q.a[i][j]=readl();
q=ksm(q,m);
for(i=1; i<=n; i++) {
for(j=1; j<n; j++) printf("%d ",q.a[i][j]);
printf("%d\n",q.a[i][n]);
}
return 0;
}
先看这个特征方程F[i] = F[i - 1] + F[i - 3],那么就有一个矩阵如下
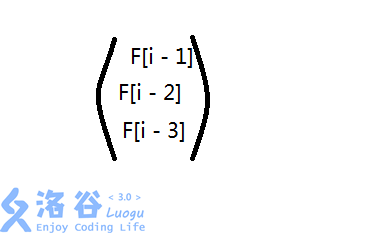
我们的目标矩阵就是
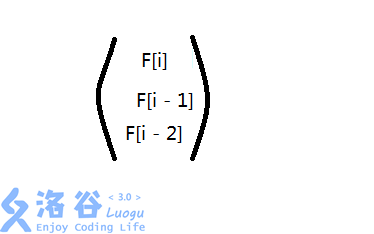
那么,针对这个矩阵我们如何转置呢?
先看目标矩阵第一个:F[i]
F[i] = F[i - 1] + F[i - 3]
那么,由矩阵乘法,转置矩阵第一行,似乎就定了:1 0 1
同样的,二三行就是1 0 0 和 0 1 0
整个矩阵如下:
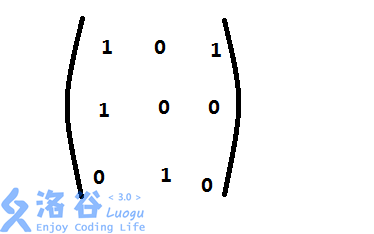
至于转置矩阵和初始矩阵的用法?
矩阵快速幂什么各种杂七杂八的

#include <iostream>
#include <cstdio>
#define LL long long
using namespace std;
inline LL read() {
LL x=0,f=1; char c=getchar();
while(c<‘0‘ || c>‘9‘) { if(c==‘-‘) f=-1; c=getchar(); }
while(c>=‘0‘ && c<=‘9‘) x=x*10+c-48,c=getchar();
return x*f;
}
const int Mod = 1000000007;
LL T,n;
struct Q {
LL a[5][5];
Q operator * (const Q &b) const {
Q ret;
for(int i=1; i<=3; i++)
for(int j=1; j<=3; j++) {
ret.a[i][j]=0;
for(int k=1; k<=3; k++)
ret.a[i][j]+=a[i][k]*b.a[k][j];
ret.a[i][j]%=Mod;
}
return ret;
}
}A,B;
inline Q ksm(Q A,LL x) {
Q ret=A,k=A;
x--;
for(; x; x>>=1,k=k*k)
if(x&1) ret=ret*k;
return ret;
}
int main() {
T=read();
while(T--) {
n=read();
if(n<=3) {
printf("1\n");
continue;
}
else {
A.a[1][1]=A.a[1][3]=A.a[2][1]=A.a[3][2]=1;
A.a[1][2]=A.a[2][2]=A.a[2][3]=A.a[3][1]=A.a[3][3]=0;
B.a[1][1]=B.a[1][2]=B.a[1][3]=1;
Q P=ksm(A,n);
printf("%lld\n",P.a[1][3]);
}
}
return 0;
}
呼~今天刚整理了这个qaq,还好还有印象。。。

#include <iostream>
#include <cstdio>
using namespace std;
const int N = 10010;
int n,m;
int dad[N];
inline int getdad(int x) {
return x == dad[x] ? x : dad[x]=getdad(dad[x]);
}
inline void Union(int u,int v) {
int f1=getdad(u),f2=getdad(v);
if(f1!=f2) dad[f1]=f2;
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1; i<=n; i++) dad[i]=i;
for(int i=1,x,u,v; i<=m; i++) {
scanf("%d%d%d",&x,&u,&v);
if(x==1) {
Union(u,v);
}
else {
int f1=getdad(u),f2=getdad(v);
if(f1!=f2) printf("N\n");
else printf("Y\n");
}
}
return 0;
}
第一次交上竟然WA了qaq,我我我我原来是更新区间的时候忘记乘以长度了qaq,再犯蠢就打我自己qaq

#include <iostream> #include <cstdio> #define mid ((l+r)>>1) #define lson rt<<1 #define rson rt<<1|1 #define LL long long using namespace std; const int M = 100001; int n,m,a,b,x,s[M]; LL ans; struct Tree { LL l,r,w,f; } t[M<<2]; inline void update(int rt) { int l=t[rt].l,r=t[rt].r; t[rt].w=t[lson].w+t[rson].w; } inline void build(int rt,int l,int r) { t[rt].l=l,t[rt].r=r,t[rt].f=0; if(l==r) { t[rt].w=s[l]; return ; } build(lson,l,mid); build(rson,mid+1,r); update(rt); } inline void down(int rt) { int l=t[rt].l,r=t[rt].r; t[lson].f+=t[rt].f; t[rson].f+=t[rt].f; t[lson].w+=t[rt].f*(t[lson].r-t[lson].l+1); t[rson].w+=t[rt].f*(t[rson].r-t[rson].l+1); t[rt].f=0; } inline void addq(int rt) { int l=t[rt].l,r=t[rt].r; if(a<=l && r<=b) { t[rt].f+=x; t[rt].w+=(t[rt].r-t[rt].l+1)*x; return ; } if(t[rt].f) down(rt); if(a<=mid) addq(lson); if(b>mid) addq(rson); update(rt); } inline void asksum(int rt) { int l=t[rt].l,r=t[rt].r; if(a<=l && r<=b) { ans+=t[rt].w; return ; } if(t[rt].f) down(rt); if(a<=mid) asksum(lson); if(b>mid) asksum(rson); } int main() { scanf("%d%d",&n,&m); for(int i=1; i<=n; i++) scanf("%lld",&s[i]); build(1,1,n); for(int i=1,q; i<=m; i++) { scanf("%d",&q); if(q==1) { scanf("%d%d%d",&a,&b,&x); addq(1); } else { scanf("%d%d",&a,&b); asksum(1); printf("%lld\n",ans); ans=0; } } return 0; }
标签:add target ref opened 乘法 iostream while matrix lld
原文地址:http://www.cnblogs.com/zxqxwnngztxx/p/7809628.html