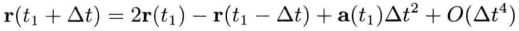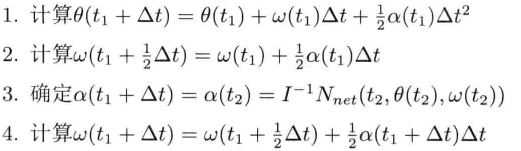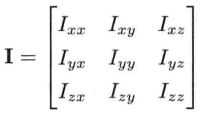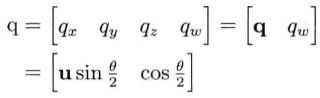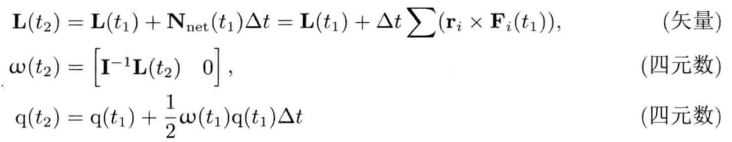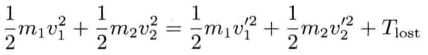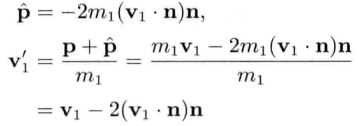标签:遍历 卡尔 异步 16px 去重 布娃娃 and 计算 微分方程
碰撞及刚体动力学
一些碰撞/物理系统:http://www.gamedev.net/community/forums/topic.asp?topic_id=463024
- I-Collide:http://cs.unc.edu/I-COLLIDE
- SWIFT:
- ODE:http://www.ode.org
- Bullet:http://code.google.com/p/bullet/
- TrueAxis:http://trueaxis.com/
- PhysX:
- Havok:
- PAL:http://www.adrianboeing.com/pal/index.ht ml
- DMM:
碰撞检测系统
物理世界
形状:
- 相交、
- 接触(分离矢量,沿该矢量运动就能高效脱离碰撞妆容)、
- 凸(由形状内发射的光线不会穿越形状两次以上)
原型:
- 球体、
- 胶囊体、
- 轴对其包围盒AABB、
- 定向包围盒OBB、
- 离散定向多胞形discrete oriented polytope DOP、
- 任意凸体积、
- 多边形汤(碰撞引擎必须和每个三角形测试)、
- 复合形状
碰撞测试:
- 点和球体相交
- 球体和球体相交
- 分离轴定理:凸形状于该轴(分离轴)上的投影不重叠,能确定两个形状不相交。分离两个物体的轴/面称为分离线/面。三维空间中,分离轴仍然是个轴,分离线变成分离面。可以把形状逐一投影到各个潜在分离轴,并检查投影区间是否相交
- AABB相交:分离轴定理。三个轴x,y,z。只有在三个轴都重叠,才是相交的。
- 检测凸碰撞:GJK算法。依赖闵可夫斯基差:把A中的所有点与B中的所有点都成对相减,得到的集合就是闵可夫斯基差。当且仅当两个形状相交,闵可夫斯基差包含原点。GJK尝试在闵科夫斯基的凸包内,尝试找出一个包含原点的四面体。若找到,则相交。
- 运动物体间的碰撞:
- 离散的静态碰撞;
- sweep shape扫琼形状做静态测试(结果不准确);
- 连续碰撞检测continuous collision detection CCD,求出最早的冲击时间TOI
性能优化:
- 利用时间一致性避免每帧重新计算一些类型的信息
- 空间划分:八叉树、二元空间分割树、kd树等
- 粗略阶段,中间阶段,精确阶段:先AABB测试哪些物体会碰撞;再用符合形状的逼近包围体检测;最终测试碰撞体中个别碰撞原形是否相交。
- 扫琼裁剪:sweep and prune,对各个膨胀提的AABB的最小,最大坐标再三个主轴上排序,然后通过遍历改有序表检测AABB之间是否重叠
碰撞查询:
- 光线投射:投射的物体并不存在于碰撞世界,不会影响其他物体。返回一个t值,P = P0(起点) + td(矢量增量)
struct RayCastContact{
F32 m_t;//此接触点的t值
U32 m_collidableId;//击中哪个可碰撞体?
Vector m_normal;//接触点的法向量
//其他信息
};
- 形状投射:传回的接触信息比光线投射更复杂,且必须返回多个接触点。
struct RayCastContact{
F32 m_t;//此接触点的t值
U32 m_collidableId;//击中哪个可碰撞体?
Point m_contactPoint;//实际接触点的位置
Vector m_normal;//接触点的法向量
//其他信息
};
- Phantom:查询碰撞体是否在其他指定体积里。对于其他碰撞体是透明的,也不参与动力学模拟。phantom会持续在碰撞世界里存在。
碰撞过滤:决定碰撞体之间的接触是否成立
- 碰撞掩码及碰撞层:对世界中物体分类,然后用一个查找表判断某类碰撞物体能否与另一些分类碰撞。
- 碰撞回调:当碰撞库检测到碰撞时调用回调函数。回调函数可以检查碰撞的具体信息,然后按自己的条件决定接受或拒绝碰撞。
- 碰撞材质:每个碰撞表面关联一组属性,它定义了某种表面在物理上和碰撞上的行为。包含碰撞属性,如音效,粒子效果,摩擦系数等等。
刚体动力学
无约束刚体指可以在3个笛卡尔轴上自由移动,并绕3个轴自由旋转,因此它含6个自由度(degree of freedom ,DOF)。
无约束刚体的运动分为两个部分:
- 线性动力学:刚体除旋转以外的运动
- 旋转动力学:刚体的旋转性运动
对于均匀密度的刚体,其质心位于刚体的几何中心;若刚体的密度不均匀,那么就要令每个小块以其质量为权值,求加权平均值作为整个刚体的质心
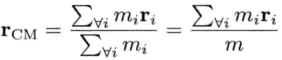
其中,
r表示半径或位置矢量,即从世界空间原点到该点的矢量。
线性动力学(质点)
运动方程求解
- 力作为函数:位置、速度、时间等的函数(常微分方程(ordinary differential equation ODE))。F(t,r(t),v(t),...) = ma(t)
- 解析解:找到闭合式函数,描述所有可能的时间值t的刚体位置(例如抛物线),但是游戏中几乎不可能。
- 数值积分:游戏引擎使用数值积分求解运动方程
- 显示欧拉:一阶近似,用切线逼近。
- 距离近似方程:r(t2) = r(t1) + v(t1)Δt
- 速度近似方程:v(t2) = v(t1) + a(t1)Δt
- 常微分方程的数值解的特性:
- 收敛性:Δt趋近于0的时候,近似解趋近真实解?
- 阶数:误差是O(t^?)
- 稳定性:数值解是否会稳定下来?
其他的数值积分方法
- 向后欧拉法
- 中点欧拉法
- Runge-Kutta方法族
- 韦尔莱积分
韦尔莱积分是三阶方法,它需要已知待求时间点的前两个Δt的位置信息或速度信息。实际上是通过泰勒展开消去重复项。
待求时间点是t1 + Δt,已知t1和t1 - Δt的位置信息。则:
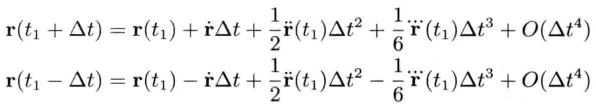
相减得到:
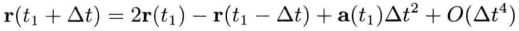
速度韦尔莱积分
- 计算r(t + Δt) = r(t1) + v(t1)Δt + 0.5a(t1)*Δt2
- 计算v(t1 + 0.5Δt) = v(t1) + 0.5a(t1)Δt
- 求a(t1 + Δt) (假设a仅仅依赖位置,如果依赖速度,则需要先计算速度近似值)a(t1 + Δt) = a(t2) = m-1F(t2,r(t2),v(t2))
- 计算v(t + Δt) = v(t1 + 0.5Δt) + 0.5a(t1 + Δt)Δt
旋转动力学(刚体)
- 二维:
- 定向:角度θ(t)(绕z轴旋转)
- 角速率&加速度:
-
- 转动惯量moment of inertia:改变角速率的难易程度。用I表示
- 力矩torque:用N表示:N = r x F
二维中力矩必然和z轴平行
二维旋转方程求解
速度韦尔莱积分
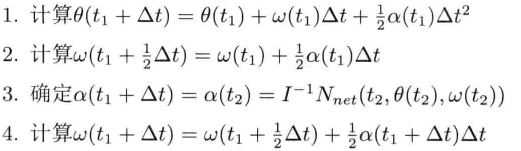
三维旋转动力学:
- 惯性张量:inertia tensor,标记为I。刚体的旋转质量由3x3矩阵表示。如果3个主轴对称,则主对角线以外的元素(也叫惯量积)就是0。物理引擎中惯性张量简化为三元素矢量[Ixx, Iyy, Izz]
刚体的定向可以用四元数q表示:
三维中的角速度:
三维旋转动力学中,一个刚体在无外力的情况下旋转,其角速度ω(t)可能不是常量,因为旋转轴方向可能会不断改变。因此角速度不守恒,但是角动量(angular momentum,表示为L)守恒。
由于ω不守恒,所以不会像线性速度一般,视角速度为一个基本的量。角速度是第二级别的量,在确定了角动量L后才计算出ω
三维力矩:N = r x F = Iα = I dω(t)/dt = d(Iω(t))/dt = dL/dt
三维旋转求解:
需要直接对L求解
将角速度转化成四元数:ω = [ωx, ωy, ωz, 0]
且:dq(t)/dt = ?ω(t))q(t)
显示欧拉:
需要定期把定向q(t)重新归一化,以消除浮点小数累计无法避免的误差。
碰撞响应
冲量碰撞响应
完全弹性碰撞无任何能量损失;完全非弹性碰撞,两个刚体一起损失动能。
- 无摩擦力下瞬时碰撞的牛顿恢复定律:假设接触点没有摩擦力,冲量必然垂直于表面法线
恢复系数:v2‘-v1‘=ε(v2 - v1)
将两者求解得

若恢复系数ε为1,刚体2的有效质量无穷大,则1/m2 = 0、v2 = 0;则:
其他碰撞响应方法
- 惩罚性力:力会在短但有限的时间内产生所需的碰撞响应。就类似一个坚硬的阻尼弹簧。它容易实现及理解,适合低速撞击,但不适合高速移动的物体。
- 约束
摩擦力
5. 休眠
将休眠物体移除模拟之外,但是仍然参与碰撞检测
条件:
- 刚体受到支持
- 刚体的线性和角动量低于阈值
- 线性和角动量的移动平均低于阈值
- 总动能(0.5p·v+0.5L·ω)低于阈值
- 逐渐减慢其运动,使其平滑的停止
Havok中有模拟岛:潜在近期会互动的物体组成。模拟岛能独立于其他岛模拟,并以整个岛为单位进入休眠。
6.约束
- 点对点约束:刚体中某个点和其他刚体的指定点对齐
- 弹簧约束:与点对点约束不同的是,它的两个点会分开一段距离
- 铰链约束:只能绕铰链旋转。
- 活塞约束:滑移铰,类似活塞一样的移动。
- 平面约束
轮子:无限旋转的铰链+阻尼弹簧加入某种形式的垂直悬挂系统
约束链:特殊群组,内含供求解程序使用的物体连接信息。模拟一长串的刚体信息。
布娃娃:刚体用约束互相链接,通常使用约束链提高模拟的稳定性。是由物理系统驱动的程序式动画。
富动力约束(powered constraint):外部引擎间接控制布娃娃的平移和定向。力+动
画,力改变动画
控制刚体的运动
- 引力
- 施加力:多数引擎设计为每帧调用一次,力的影响也在该帧内
- 施加力矩:改变速度&角速度;力偶:一样大,方向相反,离质心距离相同的对点上施加。
- 施加冲量:速度瞬间改变,无穷短时间内的施力
8.游戏对象和刚体:
物理驱动的刚体
游戏驱动的刚体(动画、玩家驱动):可当作含有无穷质量,力和力矩无法改变游戏驱动刚的速度
固定刚体:不参加动力学模拟,只有碰撞的刚体。
9.更新模拟
- 更新游戏驱动刚体
- 更新phantom
- 施以力,冲量并调整约束
- 步进模拟:
- 对运动方程数值积分,求出次帧物理状态
- 碰撞检测
- 碰撞决议
- 实行约束
- 更新物理驱动的游戏对象
- 执行phantom碰撞投射查询(以回调方式异步查询or使用上一帧的结果同步查询)
《游戏引擎架构》笔记十二
标签:遍历 卡尔 异步 16px 去重 布娃娃 and 计算 微分方程
原文地址:http://www.cnblogs.com/yeqluofwupheng/p/7717363.html
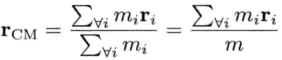 其中,r表示半径或位置矢量,即从世界空间原点到该点的矢量。
其中,r表示半径或位置矢量,即从世界空间原点到该点的矢量。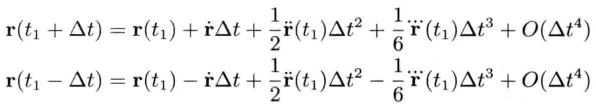 相减得到:
相减得到: