标签:表示 bool bsp eof [] std img 筛法 因此
请你想出一个算法求出n以内(含n)的所有素数,要求算法的时间复杂度越小越好。
这里介绍一种算法——快速线性素数筛法(欧拉筛法),时间复杂度O(n)。
诀窍在于:筛除合数时,保证每个合数只会被它的最小质因数筛去。因此每个数只会被标记一次,所以算法时间复杂度为O(n)。
具体请看下面的代码,主要函数是Prime(n)。
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 vector<int> Prime(int n) { // 求解n以内(含n)的素数 6 bool flag[n + 1]; // 标记数组,flag[i]==0表示i为素数,flag[i]==1表示i为合数 7 memset(flag, 0, sizeof(flag)); 8 vector<int> prime; 9 int cnt = 0; // 素数个数 10 for (int i = 2; i <= n; ++i) { 11 if (!flag[i]) { 12 prime.push_back(i); // 将i加入素数表 13 cnt++; 14 } 15 for (int j = 0; j < cnt; ++j) { // 保证每个合数只会被它的最小质因数筛去 16 if (i * prime[j] > n) break; 17 flag[i * prime[j]] = 1; 18 if (i % prime[j] == 0) break; 19 } 20 } 21 return prime; 22 } 23 int main(int argc, char const *argv[]) 24 { 25 int n; 26 while(1) { 27 printf("请输入n,将输出n以内(含n)的素数:"); 28 scanf("%d", &n); 29 if(n < 0) break; 30 vector<int> prime = Prime(n); 31 int cnt = prime.size(); 32 printf("一共有%d个素数:\n", cnt); 33 for(int i = 0; i < cnt; i++) { 34 printf("%3d ", prime[i]); 35 if(i % 10 == 9) puts(""); 36 } 37 puts("\n"); 38 } 39 return 0; 40 }
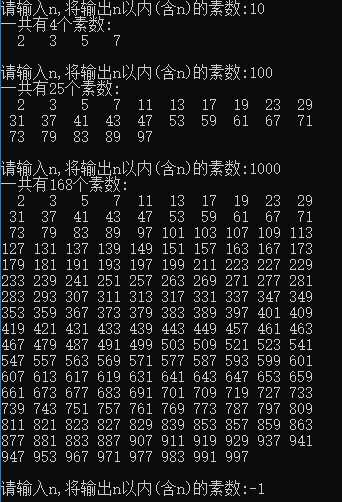
演示结果为:
标签:表示 bool bsp eof [] std img 筛法 因此
原文地址:http://www.cnblogs.com/jacen789/p/7816887.html