标签:测试 ted 全连接 images name 空间 res tempfile 3.0
卷积神经网络(Convolutional Neural Network, CNN)是一种前馈神经网络, 在计算机视觉等领域被广泛应用. 本文将简单介绍其原理并分析Tensorflow官方提供的示例.
关于神经网络与误差反向传播的原理可以参考作者的另一篇博文BP神经网络与Python实现.
卷积是图像处理中一种基本方法. 卷积核是一个nxn的矩阵通常n取奇数, 这样矩阵就有了中心点和半径的概念.
对图像中每个点取以其为中心的n阶方阵, 将该方阵与卷积核中对应位置的值相乘, 并用它们的和作为结果矩阵中对应点的值.
下面的动图展示了卷积的计算过程:
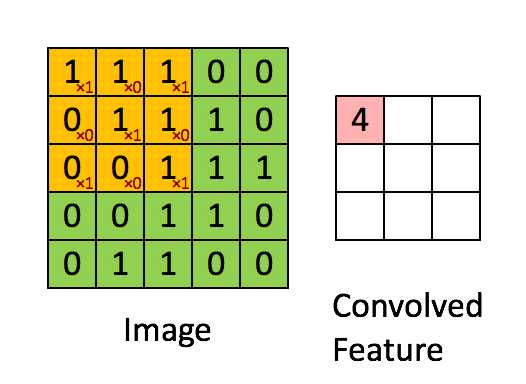
上述操作处理图像得到新图像的操作称为卷积, 卷积得到的结果矩阵被称为特征图(Feature Map). 灰度图使用一个矩阵便能表示, RGB图像则需要3个矩阵. 也就是说, 1个RGB图像使用一个卷积核卷积会得到3个Feature Map.
若卷积核中各元素和为1则图像亮度不变, 若小于1则变暗, 大于1则会变亮.
卷积核的中心无法对准原图像中边缘的像素点(与边缘距离小于卷积核半径), 若要对边缘的点进行计算必须填充(padding)外部缺少的点使卷积核的中心可以对准它们. 常用的填充策略有:
特殊的卷积核可以实现特殊的效果:
锐化

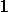

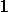

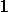





提取边缘



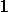
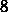

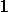

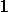




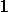

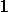
下面四张图片分别为:

一般认为人的视觉认知是从局部到全局的,而图像的空间联系也是局部的像素联系较为紧密,而距离较远的像素相关性则较弱.
同理, 每个神经元其实没有必要对全局图像进行感知, 只需要与局部图像建立连接. 在网络的更深层将神经元的局部感知进一步综合就可以了解到全局信息.
采用局部感知的方法减少了需要训练的权值数. 在实际应用中图像的分辨率和训练迭代次数都是有限的, 更少的权值数通常会带来更高精度.
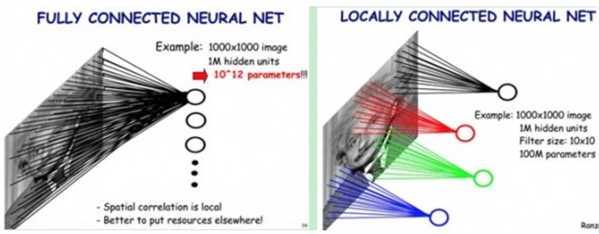
在卷积神经网络中对于同一个卷积核, 所有卷积层神经元和图像输入层的连接使用同一个权值矩阵.
权值共享进一步减少了所需训练的权值数, 一个卷积层的权值数变为了卷积核中元素个数.
权值共享隐含的原理是: 图像的一部分的统计特性与其他部分是一样的, 在图像某一部分学习到的特征也能应用到其它部分上.
从上文关于特殊卷积核的描述中可以得知, 一种卷积核通常只能提取图像中的一种特征. 且权值共享使得连接可以训练的权值数大为减少. 为了充分提取特征通常采用使用多个卷积核的方法.
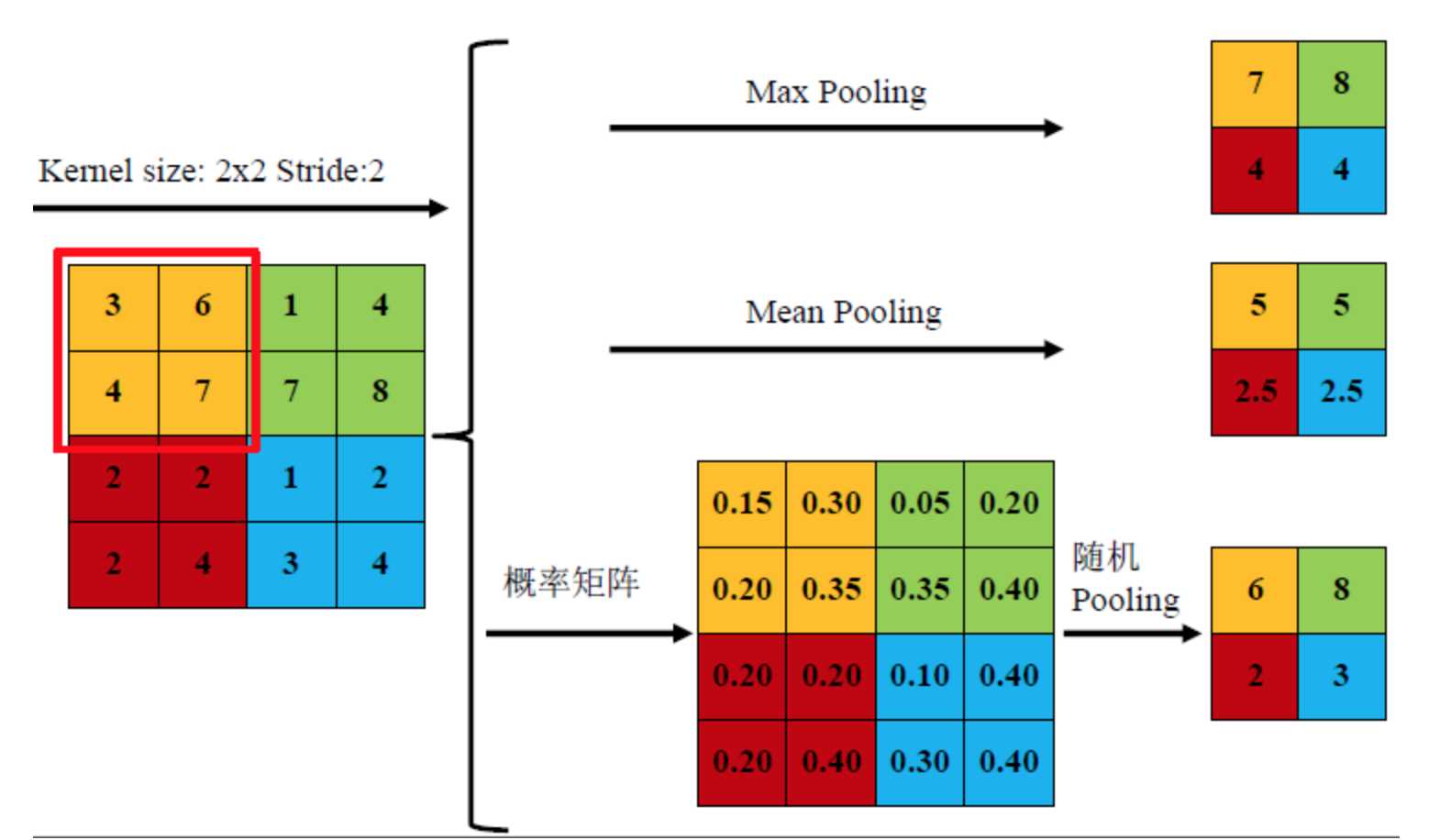
通过卷积学习到的图像特征仍然数量巨大, 不便直接进行分类. 池化层便用于减少特征数量.
池化操作非常简单, 比如我们使用一个卷积核对一张图片进行过滤得到一个8x8的方阵, 我们可以将方阵划分为16个2x2方阵, 每个小方阵称为邻域.
用16个小方阵的均值组成一个4x4方阵便是均值池化, 类似地还有最大值池化等操作. 均值池化对保留背景等特征较好, 最大值池化对纹理提取更好.
随机池化则是根据像素点数值大小赋予概率(权值), 然后按其加权求和.
TensorFlow的文档Deep MNIST for Experts介绍了使用CNN在MNIST数据集上识别手写数字的方法.
完整代码可以在GitHub上找到, 本文将对其进行简单分析. 源码来自tensorflow-1.3.0版本示例.
主要有3条引入:
import tempfile
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tfmain(_)函数负责网络的构建:
def main(_):
# 导入MNIST数据集
# FLAGS.data_dir是本地数据的路径, 可以用空字符串代替以自动下载数据集
mnist = input_data.read_data_sets(FLAGS.data_dir, one_hot=True)
# x是输入层, 每个28x28的图像被展开为784阶向量
x = tf.placeholder(tf.float32, [None, 784])
# y_是训练集预标注好的结果, 采用one-hot的方法表示10种分类
y_ = tf.placeholder(tf.float32, [None, 10])
# deepnn方法构建了一个cnn, y_conv是cnn的预测输出
# keep_prob是dropout层的参数, 下文再讲
y_conv, keep_prob = deepnn(x)
# 计算预测y_conv和标签y_的交叉熵作为损失函数
with tf.name_scope(‘loss‘):
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=y_,
logits=y_conv)
cross_entropy = tf.reduce_mean(cross_entropy)
# 使用Adam优化算法, 以最小化损失函数为目标
with tf.name_scope(‘adam_optimizer‘):
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
# 计算精确度(正确分类的样本数占测试样本数的比例), 用于评估模型效果
with tf.name_scope(‘accuracy‘):
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
correct_prediction = tf.cast(correct_prediction, tf.float32)
accuracy = tf.reduce_mean(correct_prediction)main函数与其它tensorflow神经网络并无二致, 关键分析deepnn方法如何构建cnn:
def deepnn(x):
# x的结构为[n, 784], 将其展开成[n, 28, 28]
# 第四维表示图像的特征, 当前为灰度图故为1. 也就是说每个像素点需要一个值来描述
# 类似地, RGB图像为3, RDBA图像为4
with tf.name_scope(‘reshape‘):
x_image = tf.reshape(x, [-1, 28, 28, 1])
# 第一个卷积层将28x28灰度图使用32个卷积核进行卷积
with tf.name_scope(‘conv1‘):
# 初始化连接权值, 为了避免梯度消失权值使用正则分布进行初始化
# 使用5x5大小的卷积核, 使用32个卷积核, 从原图中提取出32个特征(产生32个Feature-Map)
W_conv1 = weight_variable([5, 5, 1, 32])
# 初始化偏置值, 这里使用的是0.1
b_conv1 = bias_variable([32])
# conv2d实现: tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding=‘SAME‘)
# strides是卷积核移动的步幅
# padding有两个取值: SAME:表示卷积之后Feature-Map的长宽与x_image相同; VALID则表示忽略边缘像素, Feature-Map比x_image小
# h_conv1的结构为[n, 28, 28, 32]
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
# 第一个池化层, 将2x2方阵最大值池化为一个特征, 池化为14x14矩阵
with tf.name_scope(‘pool1‘):
h_pool1 = max_pool_2x2(h_conv1)
# 第二个卷积层, 将第一个卷积层提取32个特征使用64个卷积核提取64个特征
with tf.name_scope(‘conv2‘):
# 这里的卷积核是3维的, 有32个5*5的二维卷积核, 每个二维卷积核与一个14x14Feature-Map进行卷积
# 将这32个14x14结果矩阵累加起来便得到一个新的Feature-Map
# 64个三维卷积核得到64个新Feature-Map
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
# h_conv2的结构为[n, 14, 14, 64]
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
# 第二个池化层, 将2x2方阵最大值池化为一个特征, 池化为7x7矩阵
with tf.name_scope(‘pool2‘):
# h_pool2的结构为[n, 7, 7, 64]
h_pool2 = max_pool_2x2(h_conv2)
# 第一个全连接层, 将[7, 7, 64]特征矩阵用全连接层映射到1024各特征
with tf.name_scope(‘fc1‘):
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
# 使用dropout层避免过拟合
# 即在训练过程中的一次迭代中, 随机选择一定比例的神经元不参与此次迭代
# 参与迭代的概率值由keep_prob指定, keep_prob=1.0为使用整个网络
with tf.name_scope(‘dropout‘):
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# 第二个全连接层, 将1024个特征映射到10个特征, 即10个分类的one-hot编码
# one-hot编码是指用 `100`代替1, `010`代替2, `001`代替3... 的编码方式
with tf.name_scope(‘fc2‘):
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2
return y_conv, keep_prob请重点关注第二个卷积层的实现
整个网络暴露的接口有3个:
x[n, 784]y_conv[n, 10]keep_prob[1]现在可以继续关注main方法了, 完成网络构建之后main先将网络结构缓存到硬盘:
graph_location = tempfile.mkdtemp()
print(‘Saving graph to: %s‘ % graph_location)
train_writer = tf.summary.FileWriter(graph_location)
train_writer.add_graph(tf.get_default_graph())接下来初始化tf.Session()进行训练:
with tf.Session() as sess:
# 初始化全局变量
sess.run(tf.global_variables_initializer())
for i in range(10000):
# 每次取训练数据集中50个样本, 分10000次取出
# batch[0]为特征集, 结构为[50, 784]即50组784阶向量
# batch[1]为标签集, 结构为[50, 10]即50个采用one-hot编码的标签
batch = mnist.train.next_batch(50)
# 每进行100次迭代评估一次精度
if i % 100 == 0:
train_accuracy = accuracy.eval(feed_dict={
x: batch[0], y_: batch[1], keep_prob: 1.0})
print(‘step %d, training accuracy %g‘ % (i, train_accuracy))
# 进行训练, dropout keep prob设为0.5
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
# 评估最终精度, dropout keep prob设为1.0即使用全部网络
print(‘test accuracy %g‘ % accuracy.eval(feed_dict={
x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))启动代码会处理命令行参数和选项:
if __name__ == ‘__main__‘:
parser = argparse.ArgumentParser()
parser.add_argument(‘--data_dir‘, type=str,
default=‘/tmp/tensorflow/mnist/input_data‘,
help=‘Directory for storing input data‘)
FLAGS, unparsed = parser.parse_known_args()
tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)标签:测试 ted 全连接 images name 空间 res tempfile 3.0
原文地址:http://www.cnblogs.com/gongdiwudu/p/7821492.html