标签：pytho hub math ext idt k-means gif 随机梯度 随机梯度下降
摘要：
1.最小二乘法
2.梯度下降法
3.最大（对数）似然估计（MLE）
4.最大后验估计（MAP）
5.期望最大化算法（EM）
6.牛顿法
7.拟牛顿迭代（BFGS）
8.限制内存-拟牛顿迭代（L-BFGS）
9.深度学习中的梯度优化算法
10.各种最优化方法比较
拟牛顿法和牛顿法区别，哪个收敛快？
1.最小二乘法
注：这里假定你了解向量的求导公式，并且知道正态分布和中心极限定律（不知道的可以去数学知识索引翻翻）
(线性)最小二乘回归解法：
损失函数：平方损失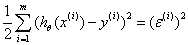
，这里的误差可能是多种独立因素加和造成的，所以我们假定其符合均值为0的高斯分布，继而可以推出平方损失。参考Andrew Ng机器学习公开课笔记 -- 线性回归和梯度下降的Probabilistic interpretation，概率解释 部分
适用场合：
优缺点：维数过高时，求逆效率过低
2.梯度下降法
这是一种迭代方法，先随意选取初始θ，然后不断的以梯度的方向修正θ，最终使J(θ)收敛到最小，当然梯度下降找到的最优是局部最优，也就是说选取不同的初值，可能会找到不同的局部最优点
常见的3终梯度下降算法：
1.批梯度下降（BGD）算法:
2.随机梯度下降（SGD）算法：
3.mini-batch随机梯度下降
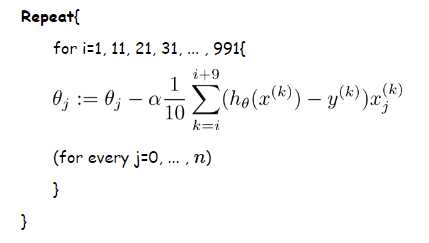
同样可以参照Andrew Ng机器学习公开课笔记 -- 线性回归和梯度下降的梯度下降（gradient descent）部分
3.最大（对数）似然估计（MLE）
参照：数理统计与参数估计杂记
4.最大后验估计（MAP）
引入了先验分布对参数做规范化，其参数估计是对贝叶斯后验概率求极值，而预测过程和最大似然估计一样
5.期望最大化算法（EM）
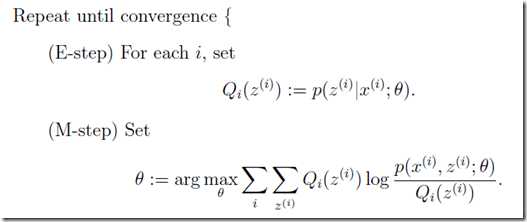
6.牛顿法：
在非线性优化问题上。牛顿法的基本思想是：在现有极小点估计值的附近对f(x)做二阶泰勒展开（如下图公式），进而找到极小点的下一个估计值,
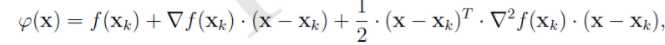
求驻点，并假设海森矩阵可逆，则得到如下迭代公式：
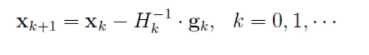
综合以上，得到牛顿发的算法流程如下：
7.拟牛顿迭代（BFGS）
同时利用梯度和二阶导数做优化，相当于在当前点处进行二阶的泰勒展开，并找到二次曲面的极小值点。
迭代公式为：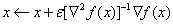
实际的优化问题中很难保证每一点的Hessian矩阵（二阶导数对应的矩阵）都正定(可逆)，而拟牛顿法构造了一个不太精确，但是可以保证正定的矩阵
Hessian矩阵的逆的更新公式是：
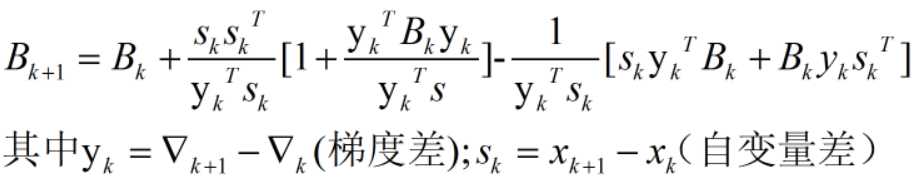
当学习速率满足Wolfe条件时，可以保证找到比现有函数更优的一个点；
Wolfe条件：
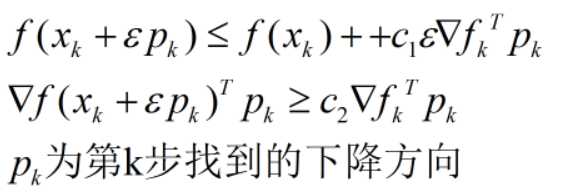
8.限制内存-拟牛顿迭代（L-BFGS）
它对BFGS算法进行了近似，其基本思想是：不在存储完整的矩阵D，而是存储计算过程中的向量s,y,需要矩阵D时,利用向量系列s,y的计算来代替。而且向量序列也不是所有的都存，
而是固定存最新的m个（参数m可由用户根据自己机器的内存自行指定）。每次计算D时，只利用最新的m个s,y.显然这样一来，我们将存储有原来的O(N*N)降到了O（mN）
9.深度学习中的梯度优化算法
算法介绍：梯度下降优化算法综述
Adam:
RMSprop: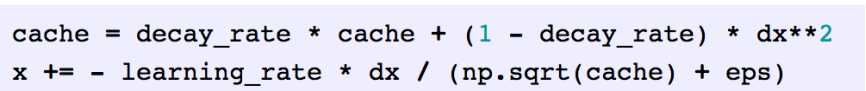
为什么adagrad适合处理稀疏梯度？它能够对每个参数自适应不同的学习速率，对稀疏特征，得到大的学习更新，对非稀疏特征，得到较小的学习更新，因此该优化算法适合处理稀疏特征数据。
10.各种最优化方法比较
1.牛顿法和拟牛顿法区别，哪个收敛快？
牛顿法:若函数的二次性态较强，牛顿法的收敛速度是很快的。但是牛顿法由于迭代公式中没有步长因子,而是定长迭代，对于非二次型目标函数，有时牛顿法不能保证函数值稳定地下降，在严重的情况下甚至不能收敛;
拟牛顿法:使用"伪逆"矩阵代替海森矩阵，所以无需计算二阶偏导，而且可以保证矩阵正定。通过一维搜索确定步长。参考链接
2.SGD,AdaGrad,Adam的区别
SGD:使用负梯度更新权重
AdaDelta和AdaGrad：1.自适应，省去了人工设定学习率的过程；2.只用到一阶信息，计算开销小；3.超参数不敏感性，其公式中额外增加的参数的选择对求解结果没有很大影响；4.鲁棒性；5.按维度分开计算学习率；
Adam:对于AdaGrad的泛化，其加入了：自适应时刻估计变量mt, μt
标签：pytho hub math ext idt k-means gif 随机梯度 随机梯度下降
原文地址：http://www.cnblogs.com/arachis/p/tools.html
