标签:最优 pack ... .com 记录 gns form 对齐 编辑
问题描述:
该问题在算法导论中引申自求解两个DNA序列相似度的问题。
可以从很多角度定义两个DNA序列的相似度,其中有一种定义方法就是通过序列对齐的方式来定义其相似度。
给定两个DNA序列A和B,对齐的方式是将空格分别插入到A和B序列中,得到具有相同长度的对齐后的序列C和D;空格可以插入到任意的位置(包括两端),但是相同位置不能同时为空格,也即是不存在C[i]和D[i]同时为空格的情况。然后为对齐后的序列的每个位置打分,总分为每个位置得分之和,具体的打分规则如下:
a、如果C[i] == D[i]且都不是空格,得3分;
b、如果C[i] != D[j]且都不是空格,得1分;
c、如果C[i] 或者D[i]是空格,得0分。
求给定原序列A和B的一个对齐方案,使得该对齐方案的总分最高。
例如,序列原序列A和B如下:
String strA = "GATC";
String strB = "ATCG";
则其中一个对齐方案如下:
GATC* *ATCG
该方案总得分score=2*0+3*3 = 9分。
实际上这是最优的对齐方案,在所有的对齐方案中总得分最高为9分。
问题分析:
为了用更加简单的方式来表示对齐的方案,我们尝试用一些特定的字符记号来表示对齐方案,对此,首先做一个约定,对于打分规则:
1、情况a用“=”字符标记;
2、情况b用“~”字符标记;
3、情况c用“*”字符标记,但是情况c实际上可以细分为两种情况:C[i]为空格时用“+”标记,D[i]为空格时用“-”号标记。这样用“+”和“-”细分的表示相比于统一用“*”来表示,本质的区别在于让对齐方案具有所谓的“方向性”,后面会看到这样的细分对于算法的实现有一定的好处。
有了这样的约定,可以将一个对齐方案用这些字符表示出来,该字符串称之为一个对齐规则字符串R。
例如上面的例子中,对齐规则就可以用字符串“-===+”来表示。
可以推断,任何两个原序列的对齐规则字符串R的长度必然满足:
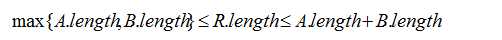
只要能够求得最优对齐方案的对齐规则字符串,就可以计算出最高分数,还可以还原出各自的对齐序列。
考察该问题的最优子结构性质,与最长公共子序列思考的角度比较类似,
用C(i,j)表示序列A[0]...A[i]和序列B[0]...B[j]的最优对齐方案的得分,不难得出其初始条件和递推求解式:

用R(i,j)表示序列A[0]...A[i]和序列B[0]...B[j]的最优对齐方案的对齐规则字符串,结合上面的递推求解式,不难推出对齐规则字符串的运算规则:

算法实现:
package agdp; public class Alignment { //根据对齐骨规则生成相应的对齐后的字符串 private static String[] generate(String base,String ...origin){ int num = origin.length; String[] align = new String[num]; for (int i = 0; i < num; i++) { if (origin[i].length() == base.length()) { align[i] = origin[i]; }else {//base.length()只能是等于或者大于两个原字符串的长度 String tmp = ""; for (int j = 0,k = 0; j < base.length(); j++) { if (base.charAt(j) == ‘+‘) { if (i == 0) {tmp = tmp+"*";} else{tmp = tmp+origin[i].charAt(k++);} }else if(base.charAt(j) == ‘-‘){ if (i == 0) {tmp = tmp+origin[i].charAt(k++);} else{tmp = tmp+"*";} } else { tmp = tmp+origin[i].charAt(k++); } } align[i] = tmp; } } return align; } public static String align(String strA,String strB){ int m = strA.length(),n = strB.length(),tmp; //aux数组记录子问题的最有对齐方案的分数,也即子问题的最高分数。 int[][] aux = new int[m+1][n+1]; //rule数组记录对齐方案,分别用"+"、"-"、"="和"~"记录四种情况。 String[][] rule = new String[m+1][n+1]; //rule初始化 rule [0][0] = ""; for (int i = 1; i < m+1; i++) { rule[i][0] = rule[i-1][0]+"-"; } for (int i = 1; i < n+1; i++) { rule[0][i] = rule[0][i-1]+"+"; } for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { if (strA.charAt(i-1) == strB.charAt(j-1)) { aux[i][j] = aux[i-1][j-1]+3; rule[i][j] = rule[i-1][j-1] + "=";//A[i]==B[j]:->"=" }else { tmp = Math.max(Math.max(aux[i-1][j], aux[i][j-1]), aux[i-1][j-1]+1); aux[i][j] = tmp; if (tmp == aux[i-1][j-1]-1) {//A[i]!=B[j]且A[i]和 B[j]不为空字符:->"~" rule[i][j] = rule[i-1][j-1]+"~"; }else if(tmp == aux[i-1][j]-2){//B[i]为空字符:->"-" rule[i][j] = rule[i-1][j]+"-"; }else{ rule[i][j] = rule[i][j-1]+"+";//A[i]为空字符:->"+" } } } } //格式化输出aux数组 for (int i = 0; i < m+1; i++) { for (int j = 0; j < n+1; j++) { System.out.format("%3d",aux[i][j]); } System.out.println(); } //格式化输出rule数组 for (int i = 0; i < m+1; i++) { for (int j = 0; j < n+1; j++) { System.out.format("%-15s",rule[i][j]); } System.out.println(); } //返回最优的对齐方法对应的规则 return rule[m][n]; } //根据规则字符串计算分数 public static int getScore(String ruleStr){ int score = 0; for (int i = 0; i < ruleStr.length(); i++) { if (ruleStr.charAt(i) == ‘=‘) { score += 3; }else if (ruleStr.charAt(i) == ‘~‘) { score += 1; } } return score; } public static void main(String[] args) { // TODO Auto-generated method stub int[] scoreAry = {3,1,0,0}; // String strA = "GATCGGCAT"; // String strB = "CAATGTGAATC"; String strA = "GATC"; String strB = "ATCG"; // String strA = "GAC"; // String strB = "ATCG"; String ruleStr = align(strA, strB); System.out.println(ruleStr); int score = getScore(ruleStr); System.out.println(score); String[] alignStr = generate(ruleStr, strA,strB); for(String str:alignStr){ System.out.println(str); } } }
还是以原始序列“GATC”和“ATCG”为例:
其子问题的得分的计算如下:
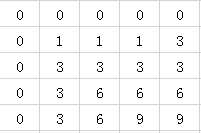
子问题的对齐规则字符串的计算如下:

需要特别注意的是,用“+”和“-”号来区分打分情况c后,对齐规则字符串是具有“方向性”的,也就是说对齐规则“-===+”是指从A->B方向的对齐规则。那如果需要B->A的对齐规则,只需要将对齐规则的字符串中+“和”-”相互替换即可。
实际上,从DNA序列对齐问题过渡到编辑距离问题是很比较自然的。本文也有意识的将这两个问题联系在一起,编辑距离问题见下一篇博文。
参考资料:
算法导论.第十五章 习题15-5
标签:最优 pack ... .com 记录 gns form 对齐 编辑
原文地址:http://www.cnblogs.com/qcblog/p/7820140.html