【搜索引擎（六）】布隆过滤器推导及应用

标签：mil   bsp   内存   es2017   精确   选中   情况下   src   数组   

介绍

    接上篇，【搜索引擎（五）】局部敏感哈希，本篇介绍的也是一个不精确的算法，用来不精确地排除重复元素。

    利用布隆过滤器，可以大大降低排重的时间。但是其实在实际中它的作用有限，还要结合其他的技巧才能达到较好的效果。另外，它本身不作为索引，如果不加处理地加以使用，在搜索引擎的快响应（小于1s）的目标中不扮演什么重要的角色。

    跟LSH一样，它其实也是线性地压缩了比较时间。以网页url去重为例，一个url可能达到上百byte, 字符串一一比较可是很要命的。所以在url去重中，将url进行哈希就可以达到想要的效果。如果以32bit为压缩的最后结果，只考虑非线性查找，压缩时间倍数达到了 25。

    原理：

        布隆过滤器的原理很简单：

　　当一个元素被加入集合时，通过K个Hash函数将这个元素映射成一个位阵列（Bitarray）中的K个点，把它们置为1。检索时，我们只要看看这些点是不是都是1就（大约）知道集合中有没有它了：

  如果这些点有任何一个0，则被检索元素一定不在；

  如果都是1，则被检索元素很可能在。

    误差率分析：

 初始状态时，Bloom Filter是一个包含m位的bit数组，每一位都为0。

        有k个不同的哈希函数，每个哈希函数会将集合中的n个元素映射到m个位中。

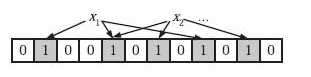
        k个哈希函数的要求是两两各自独立。

        误差率定义：

        对元素(x1, x2, x3 … xn)进行k次映射，结果bit数组中的某一位原来是0， 结果还是为0的概率(说明没有被选中)为：

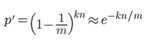
       令r为数组中0的比例，则r的数学期望E(r) = p‘, 在r已知的情况下，所求的误差率(误判为真)为：

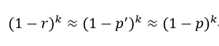
      因为1-r为1的期望比例, (1-r)^k表示某一位连续k次哈希为1的概率。

      误差率为 f = (1 – p)^k。

      为什么是false positive rate？k次哈希都选中了为1的区域，代表错误元素被判为真。由于在现实中假元素在全集中的比例远大于真元素，所以可以用这个来近似表示误差率。

  误判率最低的要求：

        现在计算对于给定的m和n，k为何值时可以使得误判率最低。设误判率为k的函数为：

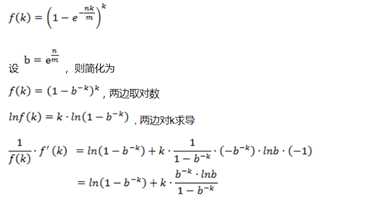
    即k在等于ln2* m / n的时候误差率最小，最小误差为：

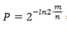
    布隆过滤器的参数确定：

        给定要加入的元素数n和误差率P, 求需要的每个元素的内存大小：

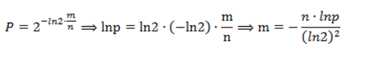
    再由m，n得到hash函数的个数：

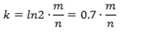
对应误差查询：

参考：

https://www.kancloud.cn/kancloud/the-art-of-programming/41619 (没有给出最优推导)

http://www.cnblogs.com/allensun/archive/2011/02/16/1956532.html (没有给出图例)

【搜索引擎（六）】布隆过滤器推导及应用

标签：mil   bsp   内存   es2017   精确   选中   情况下   src   数组   

原文地址：http://www.cnblogs.com/wangzming/p/7827425.html