标签:src 分割 分段 png 技术分享 等价 距离 哪些 思路
一个最原始粗暴的拟合任意函数的思路,是将函数切成很多段线性函数,之后用逻辑门控制当x在哪一个区间时,某些逻辑门被激活,对应的线性函数的权重w与偏移量b在逻辑门的包裹下变成非0,计算出y在这一段的输出值。
需要推导出拟合函数y=f(x)需要哪些逻辑门,以及如何使用神经网络构建这些逻辑门。
首先最简单的是开关门:
${s^{(1)}}(x) = t{\rm{ = Relu}}({\rm{1 - 1000*Relu}}({\rm{u}}))$
使用Relu激活函数构建的开关门比起使用sigmoid函数构建的开关门
${s^{(1)}}(x) = {\rm{\sigma (1000x)}}$
的作用是相同的,都是让x>0时t=1,否则t=0
通过平移技巧:f(x-p)等价于f(x)平移+p距离,可以指定门的位置。
接下来是将开关门进行与/或组合,得到的门。
假如t1负责激活x>6, t3负责激活x>9,那么定义t2 = t1 and (not t3) = ${s^{(1)}}( t1 - t3)$ ,即可用t2描述 6<x<=9的区间。
类似的,也可以定义t4 = t1 or t3 =
考虑任意函数,都可以被近似为多段线性函数。简便起见,假设三段线性函数的两个分割点是x=6以及x=9

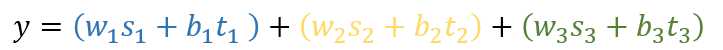
b是偏移量,t是激活门,当x落在对应分段区间i内,激活门 t_i=1,否则t_i = 0
y的值可以分拆成ws的值与bt的值。下面画出了bt与s的值。

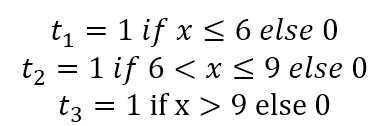
满足上述t条件的公式有:
${t_i}{\rm{ = Relu(1 - 1000 * Relu(}}{{\rm{u}}_i}{\rm{)) }}$ 对于i=1, 2, 3
${u_1} = - 1000x + 6000$
${u_2} = 1000x - 9000$
${u_3} = - 1000{t_1} - 1000{t_3} + 500$
这里通过Relu函数外加一层线性权重(w=-1000, b=1)构成了一个开关门 Relu(1-1000*Relu(x))。门的位置通过一层线性函数平移变换确定。
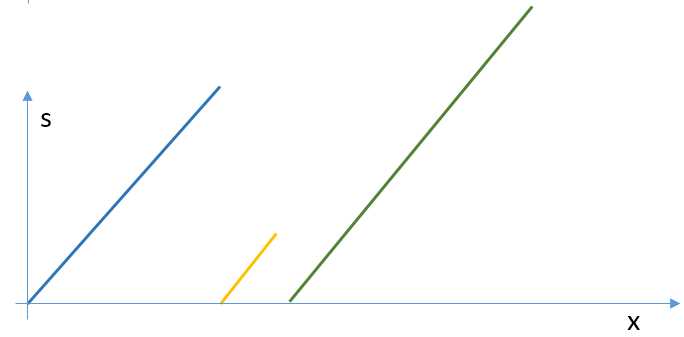
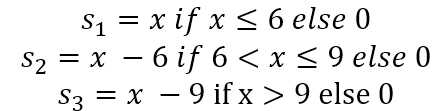
标签:src 分割 分段 png 技术分享 等价 距离 哪些 思路
原文地址:http://www.cnblogs.com/ws12345/p/7827600.html