标签:blog inline 极限 down 分享 mat math line 图像
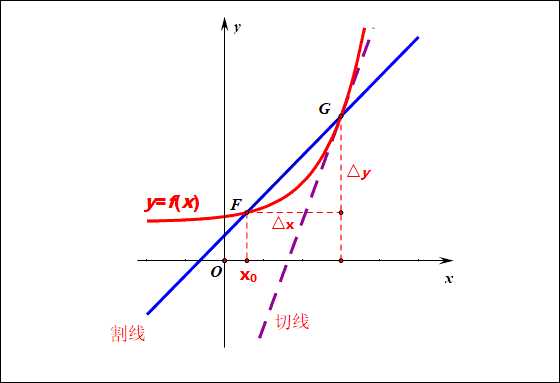
如图所示,已知函数\(y=f(x)\),给定其上的两个点\(F(x_0,y_0)\)和\(G(x_0+\Delta x,y_0+\Delta y)\),则经过这两个点的直线\(FG\),我们称为函数的割线,其斜率为\(k=\cfrac{\Delta y}{\Delta x}\), 当点\(F\)沿着函数图像向点\(G\)靠近时,即\(\Delta x\longrightarrow 0\)时,割线就变成了切线。
用数学式子表达如下:\(\lim\limits_{\Delta x \to 0} \cfrac{\Delta y}{\Delta x}\),如果这个极限存在,为常识\(k\),那么我们就称之为函数在点\(x=x_0\)的导数,记作\(f'(x_0)=\lim\limits_{\Delta x \to 0} \cfrac{\Delta y}{\Delta x}=k\)
标签:blog inline 极限 down 分享 mat math line 图像
原文地址:http://www.cnblogs.com/wanghai0666/p/7833713.html