标签:demo 出现 检测 基础上 构建 函数 左右 多个 nat
信息论大师香农给出了信息随机性的度量,称为信息墒。信息的随机性越大,信息墒就越大。假定事件s1,s2,s3……sn,它们出现的概率为p(s1),p(s2)……p(sn),则每个事件的平均不确定性用香农墒(Shannon entropy)来定义,为
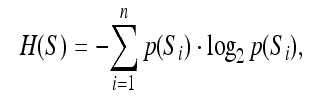
由香农墒的定义可以看出,只要把图像中的灰度值看作随机事件,就可以度量图像的信息量了。
1、对于一个灰度完全一致的图像,P(Si) = 1,图像的香农墒为0;
2、对于一个对比度很大的图像,图像的香农墒很大;假定图像一半白,一半黑,香农墒为1/2 * 2 = 1; 这个特性可以用来检测图像纹理中的缺陷,纹理均匀的地方,香农墒小;纹理缺陷的地方,香农墒大;然后在墒图像选取一个合适的阈值二值化,就可以检测出缺陷。
如果直接计算整张图的香农墒,得出来的是关于整张图像的对比度,均匀性等信息的度量,一个标量值(纹理特征);主要用于分类和识别。
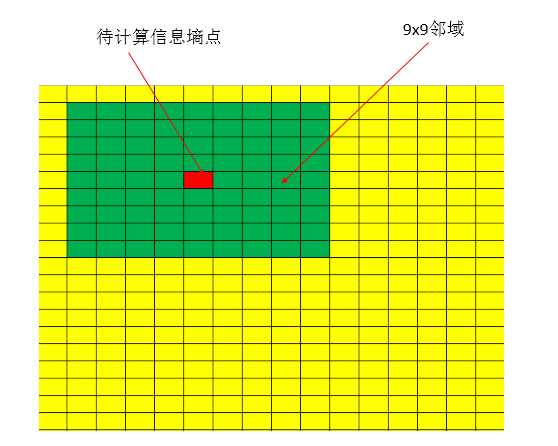
在缺陷检测中,我们更关心的是局部的特性,每个局部点的信息墒组成一个信息墒图。类似于滤波,matlab中的局部墒计算函数为entropyfilt,常用的墒滤波器是9x9大小的,因此可以按照空间域滤波滑动窗口的形式方法计算局部墒。
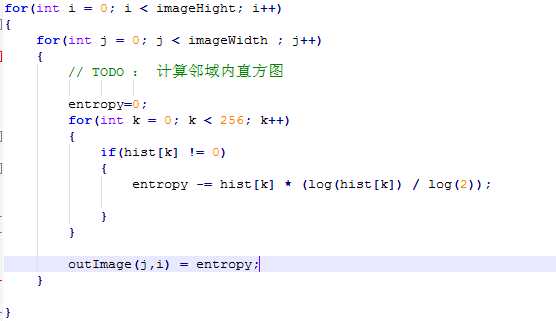
Native计算方式中最大的计算量为log(2)的重复除法
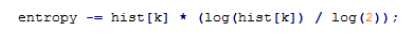
考虑到hist[k]的最大频数为81,因此计算概率的时候先不归一化处理,只计算频数,然后构建频率查找表:

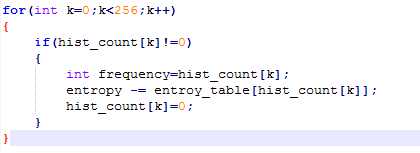
查找表方式优化效率,有质的提升。
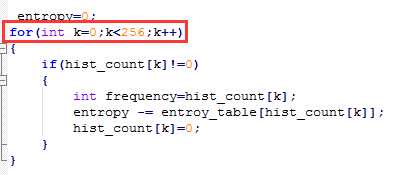
直方图中不是每个灰度频数都大于0,最多个频数大于0的个数为81,也就是邻域9x9 内的所有灰度值都不相同;因此对于那些频数为0的index可以先去除,然后在循环。测试后,提速不明显,主要是对直方图中256个index又要遍历一遍,然后还要存在索引表中,这本省要耗点时间。但对频数大于0的首尾index提取(很快就提取出来),会有10%左右的提速。
minIndex为频数不为0的最小索引值,maxIndex为频数不为0的最大索引值;
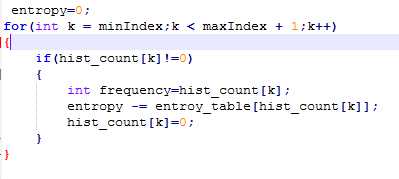
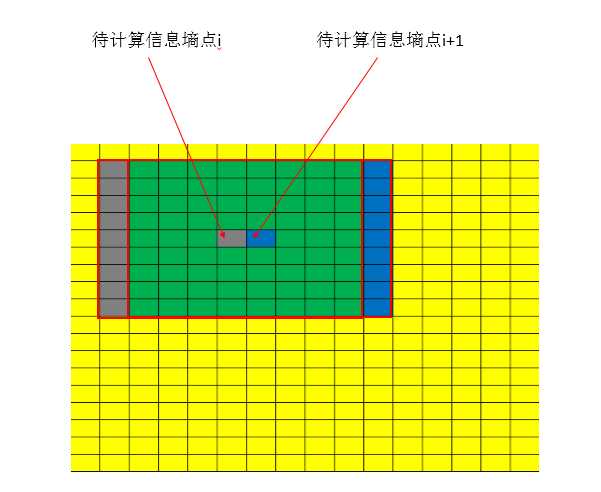
窗口在滑动时,只有第一列和最后一列是不同的元素,因此在计算下一个点邻域直方图时,只需在当前直方图的基础上减去第一列,然后在加上最后一列。这个减少了imageWidth * imageHeight * (81 - 18)次加法,600x500的图没提速前是50ms左右,提速后在40ms左右,提速20%-30%;
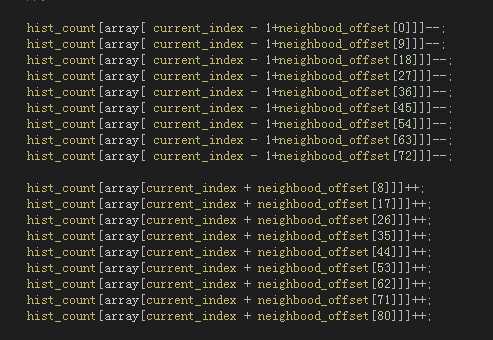





标签:demo 出现 检测 基础上 构建 函数 左右 多个 nat
原文地址:http://www.cnblogs.com/BellaVita/p/7857181.html