# 学号12 《程序设计与数据结构》第11周学习总结

教材学习内容总结

遍历

• 深度优先遍历：

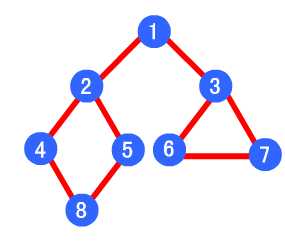
深度优先遍历，从初始访问结点出发，我们知道初始访问结点可能有多个邻接结点，深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点。总结起来可以这样说：每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。

• 特点：这样的访问策略是优先往纵向挖掘深入，而不是对一个结点的所有邻接结点进行横向访问。

• 算法步骤：

1.访问初始结点v，并标记结点v为已访问。
2.查找结点v的第一个邻接结点w。
3.若w存在，则继续执行4，否则算法结束。
4.若w未被访问，对w进行深度优先遍历递归（即把w当做另一个v，然后进行步骤123）。
5.查找结点v的w邻接结点的下一个邻接结点，转到步骤3。

• 例如：其深度优先遍历顺序为 1->2->4->8->5->3->6->7

• 广度优先遍历：

类似于一个分层搜索的过程，广度优先遍历需要使用一个队列以保持访问过的结点的顺序，以便按这个顺序来访问这些结点的邻接结点。

• 算法步骤：

1.访问初始结点v并标记结点v为已访问。
2.结点v入队列
3.当队列非空时，继续执行，否则算法结束。
4.出队列，取得队头结点u。
5.查找结点u的第一个邻接结点w。
6.若结点u的邻接结点w不存在，则转到步骤3；否则循环执行以下三个步骤：

1). 若结点w尚未被访问，则访问结点w并标记为已访问。
2). 结点w入队列
3). 查找结点u的继w邻接结点后的下一个邻接结点w，转到步骤6。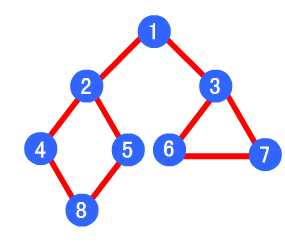

• 例如：其广度优先算法的遍历顺序为：1->2->3->4->5->6->7->8

最小生成树：

• Prim算法：

Prim算法是解决最小生成树的常用算法。它采取贪心策略，从指定的顶点开始寻找最小权值的邻接点。图G=

• Kruskal算法：

Kruskal算法是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列，接着按照顺序选取每条边，如果这条边的两个端点不属于同一集合，那么就将它们合并，直到所有的点都属于同一个集合为止。

教材学习中的问题和解决过程

• 问题1：上课最后的时候对于AOE关键路径计算不是很理解

• 问题1解决方案：和同学讨论并查阅相关资料：　
  首先，在AOE网中，从始点到终点具有最大路径长度（该路径上的各个活动所持续的时间之和）的路径为关键路径。

计算关键路径，只需求出上面的四个特征属性，然后取e(i)=l(i)的边即为关键路径上的边。
　　? Ve(j)：是指从始点开始到顶点Vj的最大路径长度

　　　计算技巧：

　　　(1)从前向后，取大值：直接前驱结点的Ｖe(j)＋到达边（指向顶点的边）的权值，有多个值的取较大者

　　　(2)首结点Ve(j)已知，为0

Vl(j)：在不推迟整个工期的前提下，事件vj允许的最晚发生时间

　　　计算技巧：

　　　(1)从后向前，取小值：直接后继结点的Ｖl(j) –发出边（从顶点发出的边）的权值，有多个值的取较小者;

　　　(2)终结点Vl(j)已知，等于它的Ve(j)）

        ?  e(i): 若活动ai由弧<vk,vj>表示，则活动ai的最早开始时间应该等于事件vk的最早发生时间。因而，有：e(i)=ve(k);（即：边（活动）的最早开始时间等于，它的发出顶点的最早发生时间） 
         ?  l(i): 若活动ai由弧<vk,vj>表示，则ai的最晚开始时间要保证事件vj的最迟发生时间不拖后。 因而有：l(i)=vl(j)-len<vk,vj>（为边（活动）的到达顶点的最晚发生时间减去边的权值）

## 代码调试中的问题和解决过程

• 问题：主要代码问题会在下周一实验报告体现。

错题及总结

• 

• 对软件的认识太过于绝对化

代码托管

结对及互评

讨论了两个遍历

本周结对学习情况

• 20162324

思考

学习还需要进一步深入

学习进度条

尝试一下记录「计划学习时间」和「实际学习时间」，到期末看看能不能改进自己的计划能力。这个工作学习中很重要，也很有用。
耗时估计的公式
：Y=X+X/N ，Y=X-X/N，训练次数多了，X、Y就接近了。

参考：软件工程软件的估计为什么这么难，软件工程 估计方法

• 计划学习时间:9小时

• 实际学习时间:8小时

• 改进情况：

(有空多看看现代软件工程 课件
软件工程师能力自我评价表)

参考资料

• 《Java程序设计与数据结构教程（第二版）》

• 《Java程序设计与数据结构教程（第二版）》学习指导