决策树

什么是决策树

决策树是一种简单高效并且具有强解释性的模型，广泛应用于数据分析领域。其本质是一颗由多个判断节点组成的树。

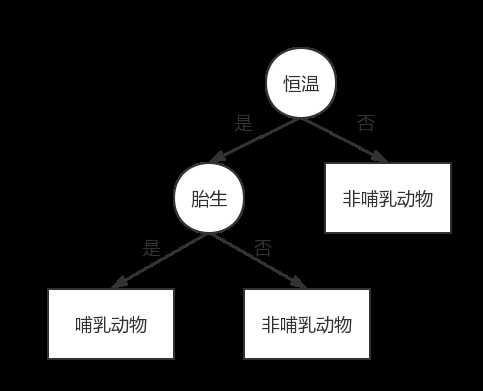
上图是一个简单的决策树模型，用来判断某个动物样本是否属于哺乳动物,树中包含三种节点：

• 根节点：没有入边，但有零条或者多条出边
• 内部节点：有一条或者多条出边
• 叶节点：只有一条入边，没有出边

在决策树中，每个叶子节点都赋予一个类标号。非叶子节点包含属性测试条件，用来分开具有不同特性的记录。

在上面的例子中，体温属性就可以把哺乳动物和非哺乳动物区分开来；如果体温是恒温的，通过是否胎生可以进一步区分哺乳动物和其他恒温动物（比如鸟类）。

一旦决策树构造完成，对记录进行分类就很容易了。从树的根节点开始，将测试条件用于检验，直到到达一个叶子节点。到达叶子节点后，这个叶子节点的类称号就被赋予这条记录。

我们现在用这颗决策树预测麻雀所属的类别：首先，麻雀是恒温动物，因此，因此，我们要检验麻雀是否是胎生，检验结果为‘否’，因此我们确定，麻雀不是哺乳动物。

决策树的构造

原则上讲，对于给定的属性集，可以构造的决策树的数目达指数级。尽管某些决策树比其他决策树更准确，但是由于搜索空间是指数规模的，找出最佳决策树在计算上是不可行的。尽管如此，人们还是开发了一些有效的算法。能够在合理的时间内构造出具有一定准确率的次最优决策树。这些算法通常都采用贪心策略，在选择划分数据的属性时，采取一系列局部最优决策来构造决策树，Hunt算法就是一种这样的算法。Hunt算法是许多决策树算法的基础，包括ID3，C4.5和CART。下面将叙述Hunt算法并讨论它的设计问题。

在Hunt算法中，通过将训练记录相继划分成较纯的子集，以递归方式建立决策树。设\(D_t\)是与结点\(t\)相关联的训练记录集，而\(y=\{y_1,y_2,...,y_c\}\)是类标号，Hunt算法的递归定义如下：

• 如果\(D_t\)中所有记录都属于同一个类\(y_t\)，则\(t\)是叶结点，用\(y_t\)标记。

• 如果\(D_t\)中包含属于多个类的记录，则选择一个属性测试条件将记录划分成较小的子集。对于测试条件的每个输出，创建一个子女结点，并根据测试结果将\(D_t\)中的记录分布到子女结点中。然后，对于每个子女结点，递归地调用该算法。

为了解释该算法如何执行，考虑如下问题:预测贷款申请者是会按时归还贷款，还是会拖欠贷款。对于这个问题，训练数据集可以通过考察以前贷款者的贷款记录来构造。下表每条记录都包含贷款者的个人信息，以及贷款者是否拖欠贷款的类标号。

该分类问题的初始决策树只有一个结点，类标号为“拖欠货款=否”,意味大多数贷款者都按时归还贷款。然而，该树需要进一步的细化，因为根结点包含两个类的记录。根据“有房者”测试条件，这些记录被划分为较小的子集。选取属性测试条件的理由稍后讨论，目前，我们假定此处这样选是划分数据的最优标准。接下来，对根结点的每个子女递归地调用Hunt算法。从给出的训练数据集可以看出，有房的贷款者都按时偿还了贷
款，因此，根结点的左子女为叶结点，标记为“拖欠贷款=否”。对于右子女，我们需要继续递归调用Hunt算法，直到所有的记录都属于同一个类为止。每次递归调用所形成的决策树如下图所示。

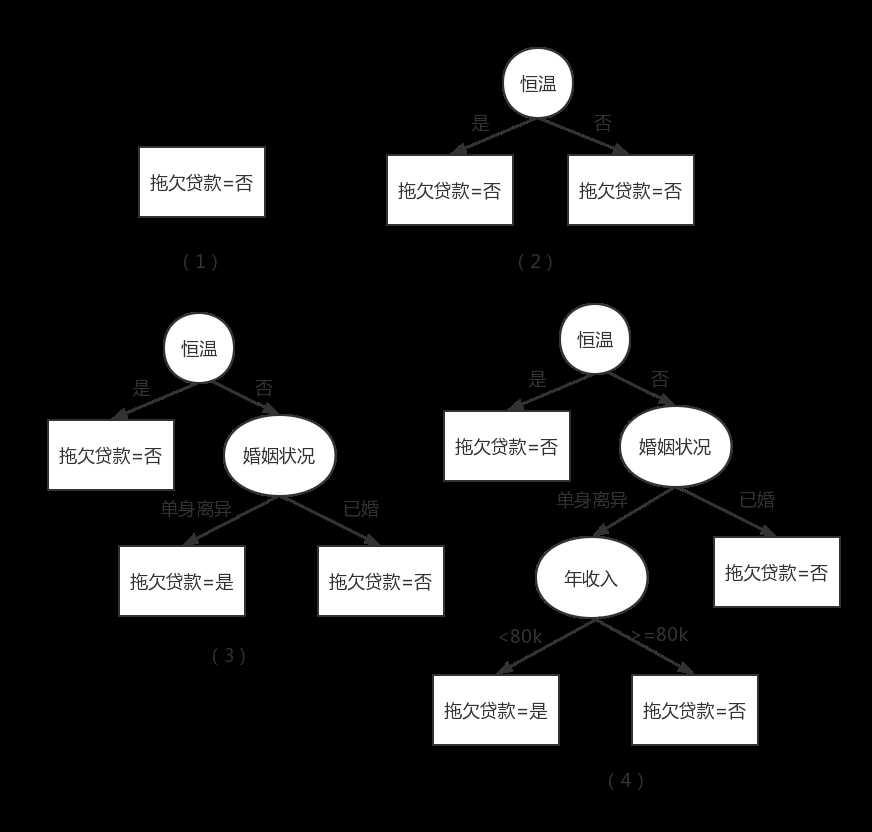
如果属性值的每种组合都在训练数据中出现，并且每种组合都具有唯一的类标号，则Hunt算法是有效的。但是对于大多数实际情况，这些假设太苛刻了，因此，需要附加的条件来处理以下的情况。

• 算法的第二步所创建的子女结点不能为空，即不存在与这些结点相关联的记录。如果没有一个训练记录包含与这样的结点相关联的属性值组合，这种情形就可能发生。这时，该结点成为叶结点，类标号为其父结点上训练记录中的多数类。
• 在第二步，如果与\(D_t\)相关联的所有记录都具有相同的属性值(目标属性除外)，则不可能进一步划分这些记录。在这种情况下，该结点为叶结点，其标号为与该结点相关联的训练记录中的多数类。

决策树归纳的学习算法必须解决下面两个问题。

• 如何分裂训练记录? 树增长过程的每个递归步都必须选择一个属性测试条件，将记录划分成较小的子集。为了实现这个步骤，算法必须提供为不同类别的属性指定测试条件的方法，并且提供评估每种测试条件的客观度量。

• 如何停止分裂过程? 需要有结束条件，以终止决策树的生长过程。一个可能的策略是分裂结点，直到所有的记录都属于同一个类，或者所有的记录都具有相同的属性值。尽管两个结束条件对于结束决策树归纳算法都是充分的，但是还可以使用其他的标准提前终止树的生长过程。

  选择最佳划分的度量

  接下来就是构造决策树的重点：选择最佳划分的度量，这也是ID3，C4.5，CART的出处。

  ID3算法

  ID3算法是构造决策树的常用算法，同时它也是C4.5和CART的基础。介绍ID3算法之前，首先要说一下信息熵和信息增益的概念。

在信息论中，期望信息越小，信息增益越大，从而纯度越高，这里纯度高的意思是不同类别的记录要分得足够开。所以ID3算法的核心思想就是根据信息增益进行属性选择，选择分裂后信息增益最大的属性进行分裂。

设\(D\)为用类别对训练元组进行的划分，则\(D\)的熵表示为

\[info(D)=-\sum_{i=1}^{m}p_ilog_2(p_i)\]

其中\(p_i\)表示第\(i\)个类别在整个训练元组中出现的概率，可以用属于此类别元素的数量除以训练元组元素总数量作为估计。熵的实际意义表示是\(D\)中元组的类标号所需要的平均信息量。

现在我们假设将训练元组\(D\)按属性\(A\)进行划分，则\(A\)对\(D\)划分的期望信息为：

\[info_A(D)=\sum_{j=1}^{v}\frac{|D_j|}{|D|}info(D_j)\]

这里\(v\)是属性\(A\)所有可能取值的个数。比如，用是否恒温检验是否为哺乳动物时，只有‘是’与‘否’两种可能取值，所以\(v=2\)。

至于信息增益，即为上两者之差：

\[gain(A)=info(D)-info_A(D)\]

ID3算法在每次需要分裂时，计算每个属性的增益率，然后选择增益率最大的属性进行分裂。

我们以贷款还款问题为例，分别用\(H,M,I\)代表是否有房，婚姻状况，年收入这三个属性，并假设年收入的划分点为80k：
|id |有房 |婚姻状况 |年收入 |拖欠贷款 |
|---|:------|:--------|:------|:-------|
|1 |是 |单身 |125k |否 |
|2 |否 |已婚 |100k |否 |
|3 |否 |单身 |70k |否 |
|4 |是 |已婚 |120k |否 |
|5 |否 |离异 |95k |是 |
|6 |否 |已婚 |60k |否 |
|7 |是 |离异 |220k |否 |
|8 |否 |单身 |85k |是 |
|9 |否 |已婚 |75k |否 |
|10 |否 |单身 |90k |是 |

\(info(D)=-0.7log_{2}0.7-0.3log_{2}0.3=0.879\)

\(info_H(D)=0.3*(-\frac{0}{3}log_{2}\frac{0}{3}-\frac{3}{3}log_{2}\frac{3}{3})+0.7*(-\frac{4}{7}log_{2}\frac{4}{7}-\frac{3}{7}log_{2}\frac{3}{7})=0.689\)

\(info_M(D)=0.4*(-\frac{2}{4}log_{2}\frac{2}{4}-\frac{2}{4}log_{2}\frac{2}{4})+0.4*(-\frac{0}{4}log_{2}\frac{0}{4}-\frac{4}{4}log_{2}\frac{4}{4})+0.2*(-\frac{1}{2}log_{2}\frac{1}{2}-\frac{1}{2}log_{2}\frac{1}{2})=0.6\)

\(info_I(D)=0.3*(-\frac{0}{3}log_{2}\frac{0}{3}-\frac{3}{3}log_{2}\frac{3}{3})+0.7*(-\frac{4}{7}log_{2}\frac{4}{7}-\frac{3}{7}log_{2}\frac{3}{7})=0.689\)

那么相应的信息增益分比为：

\(gain_H=info(D)-info_H(D_j)=0.19\)

\(gain_M=info(D)-info_M(D_j)=0.279\)

\(gain_I=info(D)-info_I(D_j)=0.19\)

由于选择婚姻状况为属性时信息增益最大，所以第一次检验条件选择婚姻状况。接下来只需处理叶子节点，或者递归调用上述步骤即可,最终可以得到整棵决策树。

C4.5算法

ID3算法在选择属性时偏向于多值属性，另外ID3不能处理连续属性，上面的例子中，我们在处理年收入属性时，认为的选择了阈值。ID3的后继算法C4.5被设计用于克服这些不足之处。C4.5算法首先定义了“分裂信息”，其定义可以表示成：

\[SplitInfo_A(D)=-\sum_{j=1}^{v}\frac{|D_j|}{|D|}log_{2}(\frac{|D_j|}{|D|})\]

其中各符号意义与ID3算法相同，然后，增益率被定义为：

\[GainRatio(A)=\frac{gain(A)}{SplitInfo(A)}\]

C4.5选择具有最大增益率的属性作为分裂属性。

在处理连续型属性时，C4.5将连续型变量由小到大递增排序，取相邻两个值的中点作为分裂点，然后按照离散型变量计算信息增益的方法计算信息增益，取其中最大的信息增益作为最终的分裂点。

CART算法

CART，又名分类回归树，是一种在ID3的基础上进行优化的二叉决策树。CART既能是分类树，又能是分类树.当CART是分类树时，采用GINI值作为节点分裂的依据；当CART是回归树时，采用样本的最小方差作为节点分裂的依据。注意，CART是二叉树。

分类树情况下，选择具有最小\(Gain_GINI\)的属性及其属性值，作为最优分裂属性以及最优分裂属性值。\(Gain_GINI\)值越小，说明二分之后的子样本的“纯净度”越高，即说明选择该属性（值）作为分裂属性（值）的效果越好。对于训练集\(D\)，\(GINI\)计算如下：

\[GINI(D)=1-\sum p_{k}^{2}\]

其中，在训练记录\(D\)中，\(p_k\)表示第\(k\)个类别出现的概率。

对于含有\(N\)个样本的训练集\(D\)，根据属性\(A\)的第\(i\)个属性值，将训练集\(D\)划分成两部分，则划分成两部分之后，\(Gain_GINI\)计算如下：

\($GainGINI_{A,i}(D)=\frac{n_1}{N}GINI(D_1)+\frac{n_2}{N}GINI(D_2)\) $

其中，\(n1,n2\)分别为样本子集\(S1,S2\)的样本个数。

对于属性\(A\)，分别计算任意属性值将数据集划分成两部分之后的\(GainGINI\)，选取其中的最小值，作为属性\(A\)得到的最优二分方案：
\[min_{i\in A}(GainGINI_{A,i}(D))\]

对于样本集\(D\)，计算所有属性的最优二分方案，选取其中的最小值，作为样本集\(D\)的最优二分方案：
\[min_{A\in Attribute}(min_{i\in A}(GainGINI_{A,i}(D)))\]

所得到的属性\(A\)及其第\(i\)属性值，即为样本集\(S\)的最优分裂属性以及最优分裂属性值。

回归树情况下，选取\(Gainσ\)为评价分裂属性的指标。选择具有最小\(Gainσ\)的属性及其属性值，作为最优分裂属性以及最优分裂属性值。\(Gainσ\)值越小，说明二分之后的子样本的“差异性”越小，说明选择该属性（值）作为分裂属性（值）的效果越好。
针对含有连续型分类结果的训练集\(D\)，总方差计算如下：

\[\sigma (D)=\sqrt{\sum{(C_k-\mu)^2}}\]

其中，\(\mu\)表示训练集\(D\)中分类结果的均值，\(C_k\)表示第\(k\)个分类结果。

对于含有\(N\)个样本的训练集\(D\)，根据属性\(A\)的第\(i\)个属性值，将训练集\(D\)划分成两部分，则划分成两部分之后，\(Gainσ\)计算如下：

\[Gain\sigma _{A,i}(D)=\sigma (D_1)+\sigma (D_2)\]

对于属性\(A\)，分别计算任意属性值将训练集\(D\)划分成两部分之后的\(Gainσ\)，选取其中的最小值，作为属性\(A\)得到的最优二分方案：

\[min_{i\in A}(Gain\sigma _{A,i}(D))\]

对于训练集\(D\)，计算所有属性的最优二分方案，选取其中的最小值，作为训练集\(D\)的最优二分方案：

\[min_{A\in Attribute}(min_{i\in A}(Gain\sigma _{A,i}(D)))\]

所得到的属性\(A\)及其第\(i\)属性值，即为训练集\(D\)的最优分裂属性以及最优分裂属性值。

决策树的优缺点

决策树的优点

• 决策树易于理解和实现，人们在通过解释后都有能力去理解决策树所表达的意义。
• 对于决策树，数据的准备往往是简单或者是不必要的，其他的技术往往要求先把数据一般化，比如去掉多余的或者空白的属性。
• 能够同时处理数据型和常规型属性。其他的技术往往要求数据属性的单一。
• 在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
• 可以处理不相关特征数据。
• 效率高，决策树只需要一次构建，反复使用，每一次预测的最大计算次数不超过决策树的深度。

• 决策树不需要相关领域知识，学习过程本身有一定的探索性。

  决策树的缺点

• 对有时间顺序的数据，需要很多预处理的工作。
• 当类别太多时，错误可能就会增加的比较快。
• 一般的算法分类的时候，只是根据一个字段来分类。
• 在处理特征关联性比较强的数据时表现得不是太好。

• 决策树的构建过程是一个递归的过程，所以需要确定停止条件，否则过程将不会结束。在决策树构造的最后一部分虽然提到过解决方案，但是很容易出现过拟合问题。

  决策树的优化

  剪枝用于解决决策树的过拟合问题，分为预剪枝（Pre-Pruning）和后剪枝（Post-Pruning）。

预剪枝（Pre-Pruning）

在构造决策树的同时进行剪枝。所有决策树的构建方法，都是在无法进一步降低熵的情况下才会停止创建分支的过程，为了避免过拟合，可以设定一个阈值，熵减小的数量小于这个阈值，即使还可以继续降低熵，也停止继续创建分支。但是这种方法实际中的效果并不好。

后剪枝（Post-Pruning）

决策树构造完成后进行剪枝。剪枝的过程是对拥有同样父节点的一组节点进行检查，判断如果将其合并，熵的增加量是否小于某一阈值。如果确实小，则这一组节点可以合并一个节点，其中包含了所有可能的结果。后剪枝是目前最普遍的做法。
后剪枝的剪枝过程是删除一些子树，然后用其叶子节点代替，这个叶子节点所标识的类别通过大多数原则(majority class criterion)确定。所谓大多数原则，是指剪枝过程中, 将一些子树删除而用叶节点代替,这个叶节点所标识的类别用这棵子树中大多数训练样本所属的类别来标识,所标识的类 称为majority class ，（majority class 在很多英文文献中也多次出现）。