标签:hbm eee uip hex bin gps clu roc 1.2
标签(空格分隔): 监督学习 线性代数
the proof of Normal equation and, before that, some linear algebra equations, which will be used in the proof.
For two matrices and
such that
is square,
.
Proof:
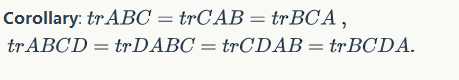
Some properties: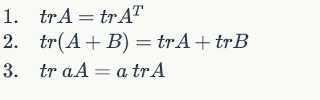
some facts of matrix derivative:
Proof:
Proof 1:
Proof 2:
Proof:
(refers to the cofactor)
(if we don’t include the intercept term)
since ,
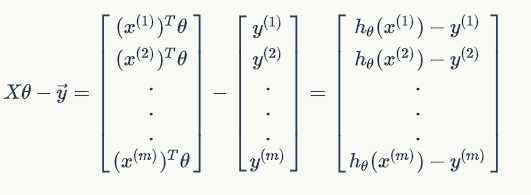
Thus,
$\frac{1}{2}(X\theta-\vec{y})^T(X\theta-\vec{y}) =
\frac{1}{2}\displaystyle{\sum{i=1}^{m}(h\theta(x^{(i)}) -y^{(i)})^2} = J(\theta) $.
Combine Equations :
Hence
Notice it is a real number, or you can see it as a matrix, so
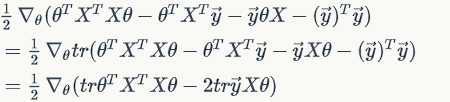
since and
involves no
elements.
then use equation with
,
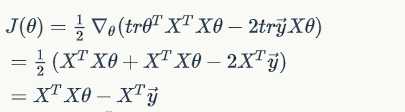
To minmize , we set its derivative to zero, and obtain the normal equation:
CS 229 notes Supervised Learning
标签:hbm eee uip hex bin gps clu roc 1.2
原文地址:http://www.cnblogs.com/EtoDemerzel/p/7881434.html