标签:技术 9.png 枚举 总数 sigma 最小值 huffman树 符号 分享


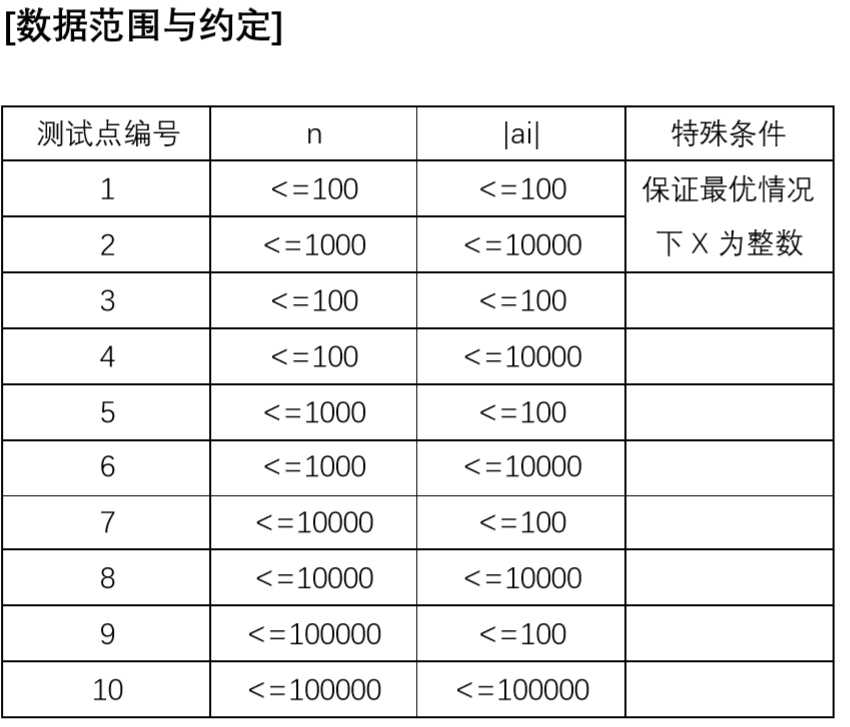
把那个sigma符号看成枚举。

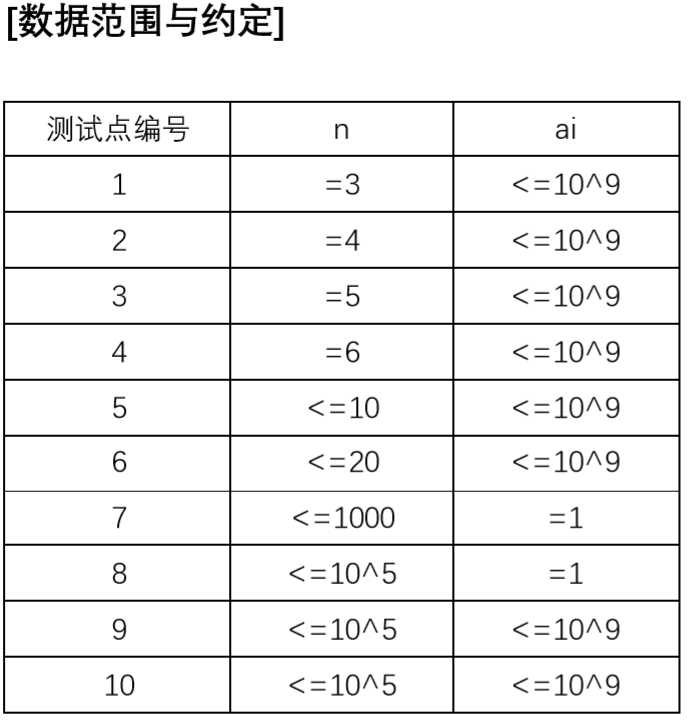
把搬砖的过程建成一棵树,根节点有所有的砖头,然后每次分成最多三个儿子。每个叶子节点可以看成每个工地。
我们可以发现,最终的答案就是每个点的点权(工地的所需砖头数)乘以深度的最小值。(根节点的深度为0)
我们想到了什么?三叉Huffman树!
由于我们要让它的深度尽量小,所以我们每个节点要尽量分3叉或者不分。
但是万一题目给出的数是偶数呢?补一个点权为0的节点,照常构造三叉Huffman树。(其实这棵树不用真正的建出来,我们只需要计算答案就行了)
还有一种思考方式:考虑到分砖头太难,我们考虑合并砖头。则题意变为:有n堆砖头,我们要把这些砖头合并成一堆。每次最多合并3堆砖头。合并的代价为你合并的砖头总数。求最小代价。
合并果子!这就比较好做,贪心,每次合并最小3堆。可是,偶数怎么办呢?
偶数就意味着你最后合并完了后只剩两堆,但这样合并一般不优啊。所以,我们就考虑先合并最小的两堆,然后3堆3堆的合。
至于为什么要合并最小的两堆,我们可以看成,这里还有一堆0个砖头,这样我们就要把这三堆合并。即先合并最小的两堆。
标签:技术 9.png 枚举 总数 sigma 最小值 huffman树 符号 分享
原文地址:http://www.cnblogs.com/lher/p/7892355.html