标签:法则 合数 解方程 images alt 导数 多少 res through
最新更新时间:2017/11/25
不定期更新
本文将进行介绍一些老师不会考诉你为什么的一些知识点,我们一个一个来。
目录:
4.杨辉三角?组合数。(待更新)
5.可重复选择的组合?(待更新)
1.关于极限0.999......等于1吗?
大多数数学老师不会考诉你,我记得我有个同学,上高一的时候问过数学老师0.999......等于1吗?然后老师很肯定的说不等于,然后就没有了。。。实际上这是一个有关于极限的问题,因为高中涉及的极限问题可以说很少了,你想想连基本函数的导数都不需要推导,只需要记住(如果你问老师这个怎么推出来的,老师会告诉你高中只要求记住,不要求推导过程,因为我就这样问过)。。。实际上0.999......是等于1的,网上的证明大概是:
由常识可知:1/3 = 0.333......
在根据等式的基本性质,对等式两边同时乘3,: 3/3 = 1 = 0.999...
得证。
这样的证明方法虽然看似正确的但是对于这个貌似没有什么太大的说服力,所以我们换一个方法:
我们可以利用方程来证明,我们设x = 0.999......
方程两边同时乘10 : 10 * x = 9.999......(没有任何问题)
因为 x = 0.999......,那么我们方程两边同时减去0.999......(也就是x):
9 * x = 9.999...... - 0.999...... = 9
解得 x = 1
所以有 0.999...... = 1
通过这个方法我们可以证明0.999......等于1,但他的用处可远不止这些。
这个方法应该是用来将无限小数化成分数的,我们可以通过这个方法将无限循环化成分数举个例子吧:
比如一道题:要求把0.978......化成分数形式。
那么我们可以设x = 0.978......
方程两边同时乘以1000(一般根据循环节长度来): 1000x = 978.978......
方程两边同时减去x(0.978......):999x = 978
所以:x = 978/999(可以验证一下,978/999是不是等于0.978......)
2.乌龟永远也追不上兔子吗?芝诺悖论。
有了上面的基础就可以看一个有趣的悖论了,这个悖论是芝诺提出的,也引发了第二次数学危机......悖论的内容大概为:
如果兔子在乌龟后面而兔子跑的比乌龟快,那么乌龟永远不会被兔子追上,芝诺是这样认为的:当兔子追到乌龟的起始位置时,乌龟会向前移动一部分距离,当兔子再一次追到乌龟上一次移动到的位置的时候,乌龟又会向前,以此类推,乌龟就不会被兔子追上了。
既然是悖论,我们思考为什么这样是错误的,我们将问题进行具体化:假如兔子速度为10m/s,乌龟速度是1m/s,兔子在乌龟后方100m,那么当兔子第一次达到乌龟的位置时时间为100/10 = 10s,此时乌龟前进10*1 = 10m,第二次达到乌龟的位置时间为10/10 = 1s,此时乌龟前进1*1 = 1m,第三次达到乌龟的位置时的时间为1/10 = 0.1s,此时乌龟前进0.1*1 = 0.1m......
这样一直下去,最后时间就是10 + 1 + 0.1 + 0.01 + 0.001 + ...... = 11.1......我们发现用100/9 = 10.1......,那么这个问题实际就是想说如果追击问题中时间一至达不到追击时间那么就永远追不上,芝诺认为这样加出来是趋近于无穷大(因为他限定了时间为11.1......之后,就一直在将11.1......进行划分)。
这里的11.1......也可以用1中介绍的方法进行转化,即将其转化成分数。
所以数学也并不是没有什么用(怎么感觉这么无力)......
3.神奇的生日聚会,真有这么高的概率吗?
这里的部分内容是从刘汝佳的《算法竞赛——入门经典》第二版中P324看到的,这里进行一个整理:
首先我们需要知道两个很基本的原理,叫做乘法原理和加法原理,这两个原理是用来计数的,我们分别举两个例子来说明这两个原理。
第一个例子:有两个空位,第一个空位可以填入1-9中任意的数字,第二个可以填入1-9中任意的数字两个空位不能不填,这样就可以组合成两位数字,问有多少个不同的两位数,答案是81,计算方法很简单,第一个空位可以填入9个数字,第二个空位也可以填入9个数字,让第一个空位中的每一个数字与第二空位中的每一个数字进行组合,可以得到不同的两位数就是9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 9 * 9 = 81。
第二个例子:现在老师给你发放了一个任务,你有2种不同的方式进行完成,第一种方式中你有3个不同的方法,第二种方式中你有3个不同的方法,问你一共有几种方法(233),答案是6,也就是3 + 3 = 6。
然后我们来看生日聚会......
有一天,你和你的好朋友“WA哈哈”去生日聚会,参加聚会的有23个人,你觉得这种聚会实在是无聊,又要给钱还吃不饱,于是too naive的你开始想一些interesting的事情,你产生了一个疑问“会不会这些宾客里有和寿星是同一天出生的,这样他不也是寿星了,interestingly!”然后你就问你的好朋友“WA哈哈”:“WA哈哈,你说这里面有人和寿星同一天生的吗?”,“WA哈哈”笑道:“你还是太天真了,才23个人,可能性接近0吧。”
“你说的有道理,但是如果换成至少有两人生日相同的概率又是多少呢?”,你笑道。
“......”,WA哈哈无语中。
然后问题就成功的被引发出来了,虽然背景有点长......我们如果考虑至少两人生日都相同并不是很好求,我们可以算出任何两个人生日不相同的概率,再用1去做差就可以得到至少两人生日相同的概率(这里至少两人的否定是没有两人),这里的原理应该是运用了集合的补集。
为了方便计算我们考虑一年有365天(即不考虑2.29出生的人),并且参加聚会的人的生日在365天中等概率选择(实际只要保证不是特意的根据参加者的生日宴请的,就可以确定为随机了)。那么任意两人生日不同的概率可以表示为:permutation(365,23)/ 365^23 = 0.4927(这里是近似值,我太弱了,不会输入“≈”)
Tips:permutation(365,23)表示365个数中中选23个方案数, 365^23表示23个365相乘。
来解释一下吧,因为有23个人每个人的生日都是从365天中随机获得,那么我们根据乘法原理就可以知道,23个人的所有方案数就是365 * 365 * 365 ...... (23个365),既然是要让每个人的生日的不相同,我们就有permutation(365,23)的方案数让任意两个人生日不同,考虑一下permutation(365,23)等于多少,第一个人的生日有365种选法,第二个人因为不能和第一个人选一样的,只有364种选法(即不选第一个人的生日)......那么最后用乘法原理进行汇总,就是365 * 364 * ...... * 343 = 很大的一个数(手动滑稽)
然后最会的概率应该用1 - 0.4927 = 0.5073(还是近似值,因为0.4927是近似值233)。哇,有至少两个人生日相同的概率竟然这么大。
4.杨辉三角?组合数。
5.可重复选择的组合?
6.孤独的根号二?无理数。
在某年某月某日某街,你无聊的在街道里寻觅着,一些疑似伟大的数学发现......,一张A4纸飘到你的脸上,你:“......”
正当你要扔掉A4纸的时候,你看着A4纸的长宽,“嗯?”(你开始疑问),然后用游标卡尺量出了长宽分别为:297mm和210mm,你用297/210 = 1.4142857142857这不是和√2(√2=1.4142135623730950488016887242097......)差不多吗?你陷入了沉思,这是为什么了呢,“从小被称为无理数的√2,怎么会和A4纸扯上关系?等等,√2为什么是无理数呢?”
来思考第一个问题:√2为什么是无理数。首先可以知道1 < √2 < 2(别问我为什么),所以说√2肯定不是整数(就是这么果断),因为有理数分为整数,有限小数,无线循环小数,我们只需要证明没有一个有限小数且没有一个无限循环小数的平方等于2就可以了,我们也可以证明分数(分母不为一)的平方一定不是整数,这里需要知道任意一个有限小数可以通过最开始介绍的方法化成分数,分数(形如a/b,a和b最大公约数为1)一定可以化成整数,或有限小数和无线循环小数,证明方法如下:
首先定义一个运算符(可能不是很准确):对于整数a % b表示a 除以 b 的余数举个栗子: 7 % 5 = 2;
7 % 5 = 2;
然后我们考虑为什么分数(整数相除)一定可以化成有限小数或无限不循环小数,考虑到除法,对于a,b(整数)相除,我们需要从高位开始算出余数(也就是a%b),如果余数为0,就代表可以除尽,否则我们就将余数乘以十再用获得的数来除以b,考虑什么时候回开始循环,当且仅当此次计算的余数在之前出现过,就会进入循环,因为余数的范围是:0 - (除数-1),这里也就是0 - (b-1)一共有b种不同的余数,因为此时我们讨论的是无限小数(既不考虑余数为0),那么对于计算b-1次后,一定会出现一个余数已经计算过了,此时就进入了循环。
我们接着正题讲“如何证明”,对于有理数我们将其写成a / b的形式,这里a,b均为整数并且互质(最大公因数为1)且分母不为1(为1就是整数了),这里介绍一个定理——唯一分解定理,内容如下:
对于任意一个大于1的正整数,可以将其写成一个或者多个质数之积的形式(此定理是欧几里得提出的,也就是小学讲的分解质因数,我们将这些质数称为它的质因子,我不会证明)。
有了这个定理我们可以推导一个结论对于一个正整数a(大于1)将其平方后不会增加它的质因子种类,只会增加数量,比如我们将144 分解 :144 = 2 * 2 * 3 * 2 * 2 * 3,然后平方得到144 * 144 = (2 * 2 * 3 * 2 * 2 * 3)^ 2,这里用幂的运算法则可以发现没有增加新的质因子。
有什么用?(我要这结论有什么用),有了这个定理,我们可以推导出一个结论,对于两个互质的正整数a,b那么一定有a*a,b*b互质(因为质因子的种类并没有增加)。有了这个就可以证明√2是无理数了,考虑对于任何有理数p,我们将其转换成分数形式:a/b(a,b互质),那么他的平方为:a*a/b*b(a*a与b*b还是互质)那么如果a/b是由有限小数转换过来,那么平方后还是有限小数,如果是整数,平方后就是整数,如果是无限循环小数那么平方后还是无限循环小数,也就是有限小数和无限循环小数的平方一定不是整数,所以√2一定不是有限小数和无限循环小数,也就是说2不是有理数的平方,所以√2一定是无理数。
如果这样不是很好理解,我们看看反证法(欧几里得给出的证明方法):
假设√2是有理数,那么√2一定可以化成a/b的形式(a,b互质,且b不为1,a和b均为正整数)
将两边平方有:2 = a*a / b*b
因为a,b互质,那么a*a和b*b依然互质
而上面的与这句话矛盾,那么推导没有问题,则假设错误,也就是√2是无理数。
证明了√2是无理数,考虑一下为什么A4纸的长宽之比如此接近√2,实际上不只是A4的长宽之比是√2,所有的Ax纸都是这样的,为什么?
关于A0纸的定义是长宽之比为√2且面积为100㎡的纸,而Ax纸就是Ax-1纸将长对折后得到的(x >= 1),那么为什么要这样定义呢?因为A级纸要求对折后长宽之比依然不变,看这个图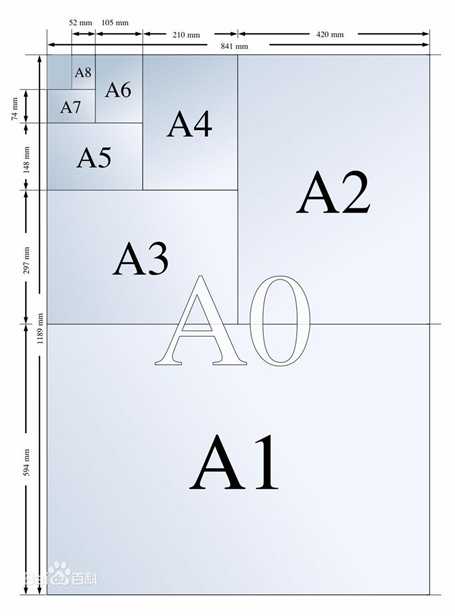 (来自百度)
(来自百度)
我们来看看为什么长宽之比为√2的纸对折后长宽之比依然不变:
设长为a则宽为√2/2*a
对折后长:√2/2*a宽:a/2(a/2 < √2/2*a)
那么√2/2*a / (a/2) = √2
我们也可以通过解方程来看:
设长宽之比为x的纸对折后长宽之比依然不变,设宽为b则长为x*b
对折后:长宽变成:x*b/2 和 b
考虑如果x*b/2 = x*b此时x无解则不可能
考虑如果x*x*b/2 = b解得x = √2或x = - √2(舍去)
呀!原来A4纸有这么多神奇得数学关系。
标签:法则 合数 解方程 images alt 导数 多少 res through
原文地址:http://www.cnblogs.com/zzozz/p/7866305.html