实验四 图的实现和应用 实验报告 20162305

实验一 邻接矩阵实现无向图

实验要求

• 用邻接矩阵实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器。给出伪代码，产品代码，测试代码（不少于5条测试）

实验过程

• 用邻接矩阵表示无向图，首先我们先明确什么是邻接矩阵。邻接矩阵就是用矩阵的方式来表示不同结点之间的关系，对于无向图来说，如果结点（i,j）之间有联系，则在矩阵中（i,j）所对应的的点的值为1，否则为0。对于邻接矩阵表示有向图，有关联的结点值对应在矩阵上的值为两者之间的权值，无关联的对应值为无穷大。想要建立一个邻接矩阵，我们需要定义好边和结点，再根据边的关系确定好对应结点之间的值。下面分析各个方法的实现。

（一）添加和删除结点

• 首先，我利用Java中的ArrayList类，生成一个vertexList用来存储结点，这样就可以利用ArrayList中自带的add方法和remove方法来实现结点的删除和添加功能。
• 相关代码

   //插入结点
    public void insertVertex(Object vertex) {
        vertexList.add(vertex);
    }

    //删除结点
    public void deleteVertex(Object vertex) {
        vertexList.remove(vertex);
    }

（二）添加和删除边

• 首先我先定义了一个int类型数组用来存储边，在添加和删除的方法中定义来了边的位置参数v1，v2，用来确定添加或删除的边的位置，添加一条边（v1,v2），则这条边在数组中对应的值为1，删除一条边（v1,v2），则这条边在数组中对应的值为0，若是想要删除的这条边不存在，那么就打印这条边不存在。
• 相关代码

    //插入边
    public void insertEdge(int v1, int v2) {
        edges[v1][v2] = 1;
        numOfEdges++;
    }

    //删除边
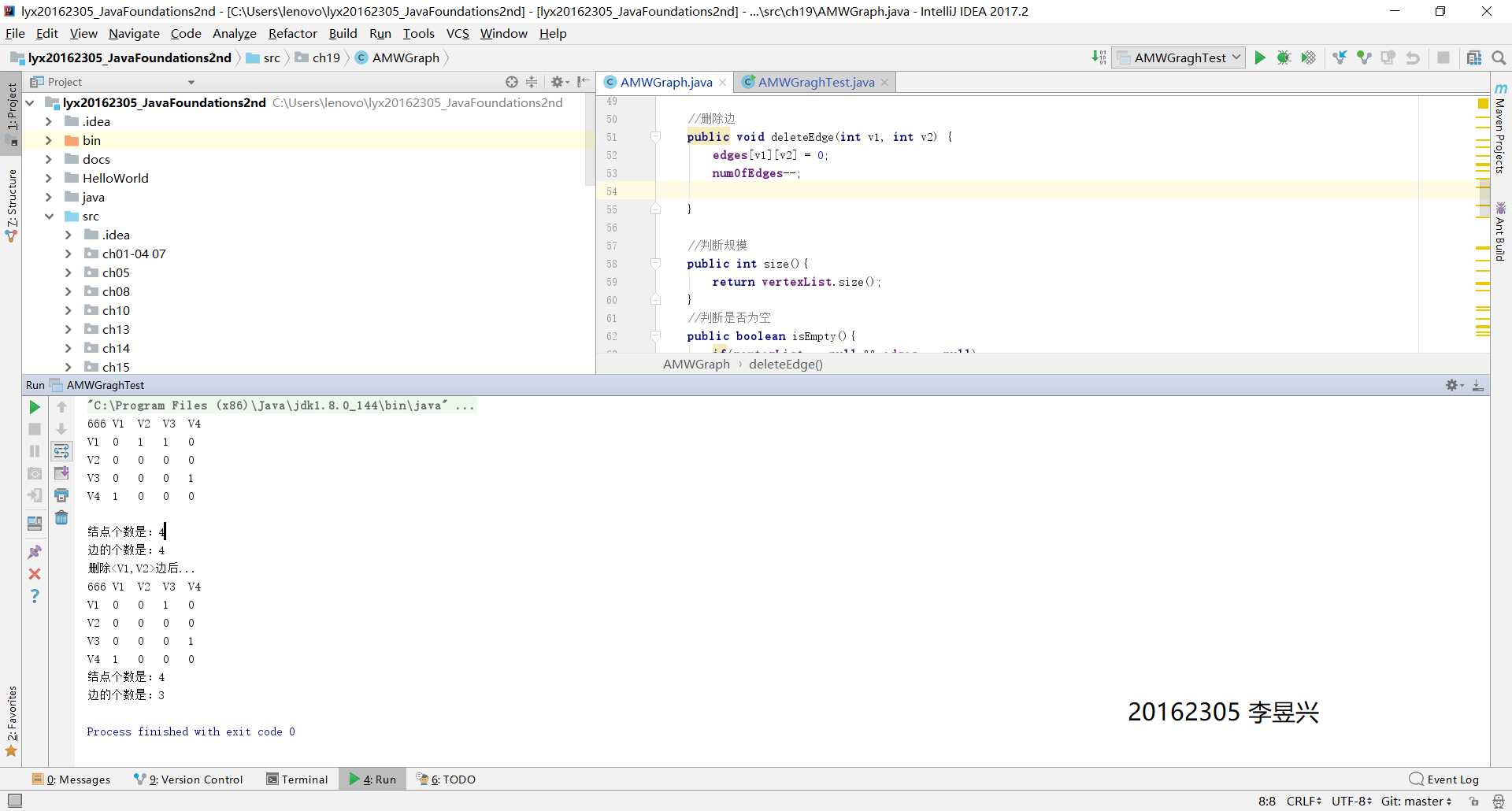
    public void deleteEdge(int v1, int v2) {
        edges[v1][v2] = 0;
        numOfEdges--;
        if (edges[v1][v2] == Integer.parseInt(null)) {
            System.out.print("该边不存在。");
        }
    }

（三）size方法

• 返回存储结点的vertex的规模，确定规模。
• 相关规模

 public int size(){
        return vertexList.size();
    }

（四）isEmpty()方法

• 判断是否为空，如果存储结点的vertexList和存储边的edges都为空，则返回true，否则返回false。
• 相关代码

 public boolean isEmpty(){
        if(vertexList == null && edges == null)
            return true;
        else
            return false;
    }

（五）广度优先迭代器

• 广度优先遍历，从一个顶点开始，辐射状地优先遍历其周围较广的区域，故称之为广度优先遍历。实现广度优先遍历，需要一个队列来保存遍历过的顶点顺序，以便按出队的顺序再去访问这些顶点的邻接顶点。我按照老师课堂讲义中给出的伪代码写出了这个方法。首先定义参数，数组visited中对应的参数位置为1，初始化队列Q；visited[N]=0；访问顶点v；visited[v]=1；顶点v入队列Q；当队列不为空的时候，弹出得到未访问的邻接点，再将得到的邻接点赋给result再回到队列，然后再判断是否队列中的元素是否都已经标记，最后打印result。

    //进行广度优先遍历的内部递归调用方法使用
    public void bfs(int i) {
        MyQueue queue = new MyQueue(100);
        System.out.print(i + " ");
        int visited[] = new int[vertexList.size()];
        for(int j= 0;j<visited.length;j++) {
            visited[j] = 0;
            queue.insert(i);
            visited[i] = 1;
            String result = vertexList.get(j) + " ";
            while (!queue.isEmpty()) {
                j = queue.peek();
                // 得到未访问过的邻接点
                int unvisitedVertex = getUnvisitedVertex(j);
                if (unvisitedVertex == -1) {
                    queue.remove();
                } else {
                    vertexList.get(unvisitedVertex);
                    result += vertexList.get(unvisitedVertex) + " ";
                    queue.insert(unvisitedVertex);
                }
                for (int i1 = 0; i1 < visited.length; i1++) {
                    if (vertexList.get(i1)!= null) 
                        if (visited[i1] != 0) {
                        queue.insert(i1);
                        visited[i1] = 1;
                    }
                }
            }
            System.out.print(result);
        }
    }

• 获取未访问顶点的方法，利用for循环判断，如果边存在可是结点对应值为null则返回i，循环结束得到为访问的顶点。

  //bfs中获取未访问的
    public int getUnvisitedVertex(int v) {
        for (int i = 0; i < numOfEdges; i++) {
            if(edges[v][i] == 1 && vertexList.get(i) == null) {
                return i;
            }
        }
        return -1;
    }

（六）深度优先迭代器

• 图的深度优先搜索，类似于树的先序遍历，所遵循的搜索策略是尽可能“深”地搜索图。如果它还有以此为起点而未探测到的边，就沿此边继续探寻下去。一直进行到已发现从源节点可达的所有节点为止。
• 深度优先遍历的内部递归方法,遍历结点和bian

    //深度优先遍历
    public void depthFirstSearch(int v) {       //驱动函数
        boolean visited[] = new boolean[vertexList.size()];
        for (int i = 0; i < vertexList.size(); i++) {
            visited[i] = false;
        }
        dfs(v, visited);                         //把每个结点遍历一次。
        System.out.println();
    }

    //进行深度优先遍历的内部递归方法使用
    private void dfs(int i, boolean visited[]) {  //工作函数
        System.out.print(i + " ");
        visited[i] = true;
        for (int j = 0; j < vertexList.size(); j++) {
            if (edges[i][j] != 0 && edges[i][j] != vertexList.size() && !visited[j]) {
                dfs(j, visited);
            }
        }
    }

实验成果截图

实验二 十字链表实现无向图

实验要求

• 用十字链表实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器；
  给出伪代码，产品代码，测试代码（不少于5条测试）

实验过程

• 十字链表是有向图的另一种存储结构，目的是将在有向图的邻接表和逆邻接表中两次出现的同一条弧用一个结点表示，由于在邻接表和逆邻接表中的顶点数据是相同的，则在十字链表中只需要出现一次，但需保留分别指向第一条"出弧"和第一条"入弧"的指针。
• 十字链表除了结构复杂一点外，其创建图的时间复杂度是和邻接表相同的，用十字链表来存储稀疏有向图，可以达到高效存取的效果，因此，在有向图的应用中，十字链表也是非常好的数据结构模型。

（一）添加和删除结点

• 首先先自己写一个Node类，定义一个新的结点。再定义一个ArrayList类中的结点node，利用带有的add方法添加入node，返回添加后的node

   public boolean addNode(Object data){
        Node a = new Node(data);
        return node.add(a);
    }

• 删除结点，先定义一个boolean类型的result为false，遍历整个node，如果找到要删除的结点，则remove删除，result为true，返回result结束。

 public boolean removeNode(Object data){
       boolean result = false;
       for (int i = 0;i<node.size();i++) {
           if (data == node.get(i).data)
           node.remove(data);
           result = true;
       }
       return result;
   }
 

（二）添加和删除边

• 十字链表中的添加边和删除边的操作，比起邻接矩阵的算法要复杂一些。十字链表中的元素由弧头、弧尾，同弧头和同弧尾这四个部分，每次删除和添加，各个部分的指针指向都有变化，都要发生相应的改变。具体操作在伪代码中显示。
• 相应代码

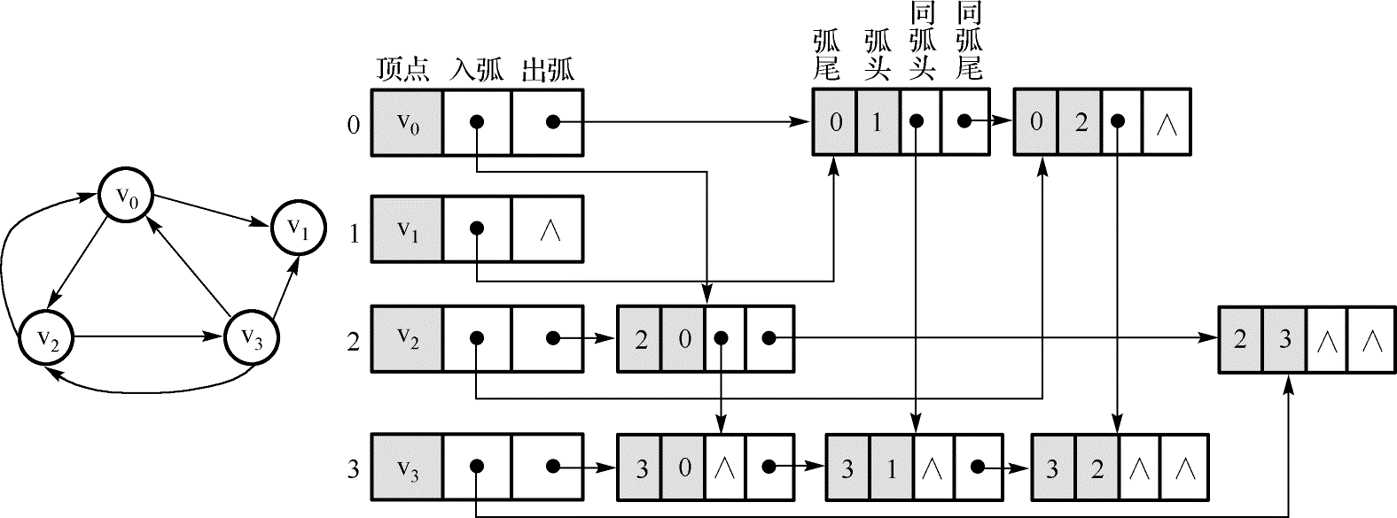
public void add (Edge<Integer> edge){
        int fromVertexIndex = edge.fromVertexIndex;
        int toVertexIndex = edge.toVertexIndex;
        Node <E, T> fromVertex = node.get(fromVertexIndex);
        Node <E, T> toVertex = node.get(toVertexIndex);

        if (fromVertex.firstOut == null) {
            //插入到顶点的出边属性

            fromVertex.firstOut = (Edge <T>) edge;
        } else {
            // 插入到edge的nextSameFromVertex属性

            Edge<Integer> tempEdge = (Edge <Integer>) fromVertex.firstOut;
            //找到最后一个Edge

            while (tempEdge.nextSameFromVertex != null) {
                tempEdge = tempEdge.nextSameFromVertex;
            }
            tempEdge.nextSameFromVertex = edge;
        }
        if (toVertex.firstIn == null) {
            //插入到顶点的入边属性

            toVertex.firstIn = (Edge <T>) edge;
        } else {
            // 插入到edge的nextSameToVertex属性

            Edge<Integer> tempEdge = (Edge <Integer>) toVertex.firstIn;
            //找到最后一个Edge

            while (tempEdge.nextSameToVertex != null) {
                tempEdge = tempEdge.nextSameToVertex;
            }
            tempEdge.nextSameToVertex = edge;
        }
    }

 public void removeEdge(int a,int b){
        Edge <T> node1;
        Edge <T> node2;
        node1 = node.get(a).firstOut;
        node2 = node.get(b).firstIn;
        if(node1.toVertexIndex==b)
            node.get(a).firstOut = node1.nextSameToVertex;
        else {
            while (node1.nextSameToVertex.toVertexIndex!=b){
                node1 = node1.nextSameToVertex;
            }
            node1.nextSameToVertex = (node1.nextSameToVertex).nextSameToVertex;
        }
        if (node2.fromVertexIndex == a){
            node.get(b).firstIn = node1.nextSameFromVertex;
        }else {
            while (node2.nextSameFromVertex.fromVertexIndex != b){
                node2 = node2.nextSameFromVertex;
            }
            node1.nextSameFromVertex = (node1.nextSameFromVertex).nextSameFromVertex;
        }
    }

(三)广度优先迭代器

• 广度优先迭代器的实现方式同实验一的实验方法类似，本次是在ArrayList的基础上实现的。

 public ArrayList<E> bfs(int a) {
        //初始化队列
        LinkedQueue linkedQueue = new LinkedQueue();
        //设立一个访问标志数组
        int[] visited = new int[node.size()];
        //设立list
        ArrayList<E> list = new ArrayList<E>();
        int current;
        Edge <T> headNode = null;
        //未访问的元素标记为0
        for (int i = 0; i<visited.length;i++){
            visited[i] = 0;
        }
        //标记访问a
        linkedQueue.enqueue(a);
        //访问后标记为1
        visited[a] = 1;

        while (!linkedQueue.isEmpty()){
            current = (int) linkedQueue.dequeue();
            list.add(node.get(current).data);
            for (int j = 0;j<visited.length;j++)
                headNode = node.get(j).firstOut;
            while (headNode!=null){
                if (visited[headNode.toVertexIndex] == 0) {
                    linkedQueue.enqueue(headNode.toVertexIndex);
                    visited[headNode.toVertexIndex] = 1;
                }
                headNode = headNode.nextSameToVertex;
            }
        }
        return list;
    }

(四)size方法

• 返回node的大小

 public int size(){
        return node.size();
    }

(五)isEmpty方法

• 判断结点集是否为空，如果为空返回true，不为空返回false。

  public boolean isEmpty(){
        if (node.size() == 0)
            return true;
        else
            return false;
    }

实验成果截图

实验三 最短路径问题

实验要求

• 创建计算机路由系统，输入网络中点到点的线路，以及每条线路使用的费用，系统输出网络中各点之间最便宜的路径，指出不相通的所有位置

实验过程

• 这个实验的要求实质是利用算法实现最短路径，我用的是dijkstra算法实现的。
• 原理（来自搜狗百科）
• 
• 相关代码

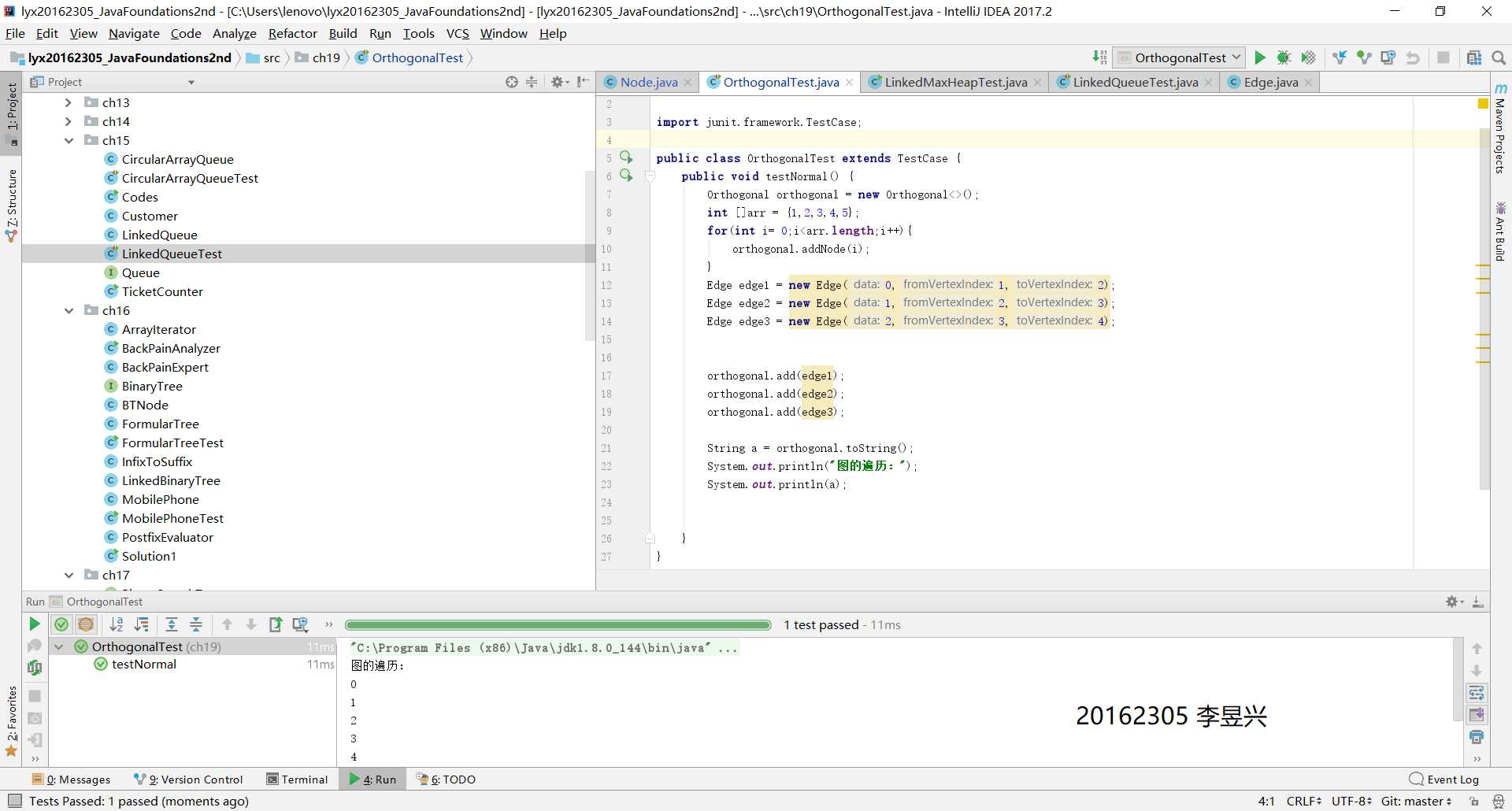
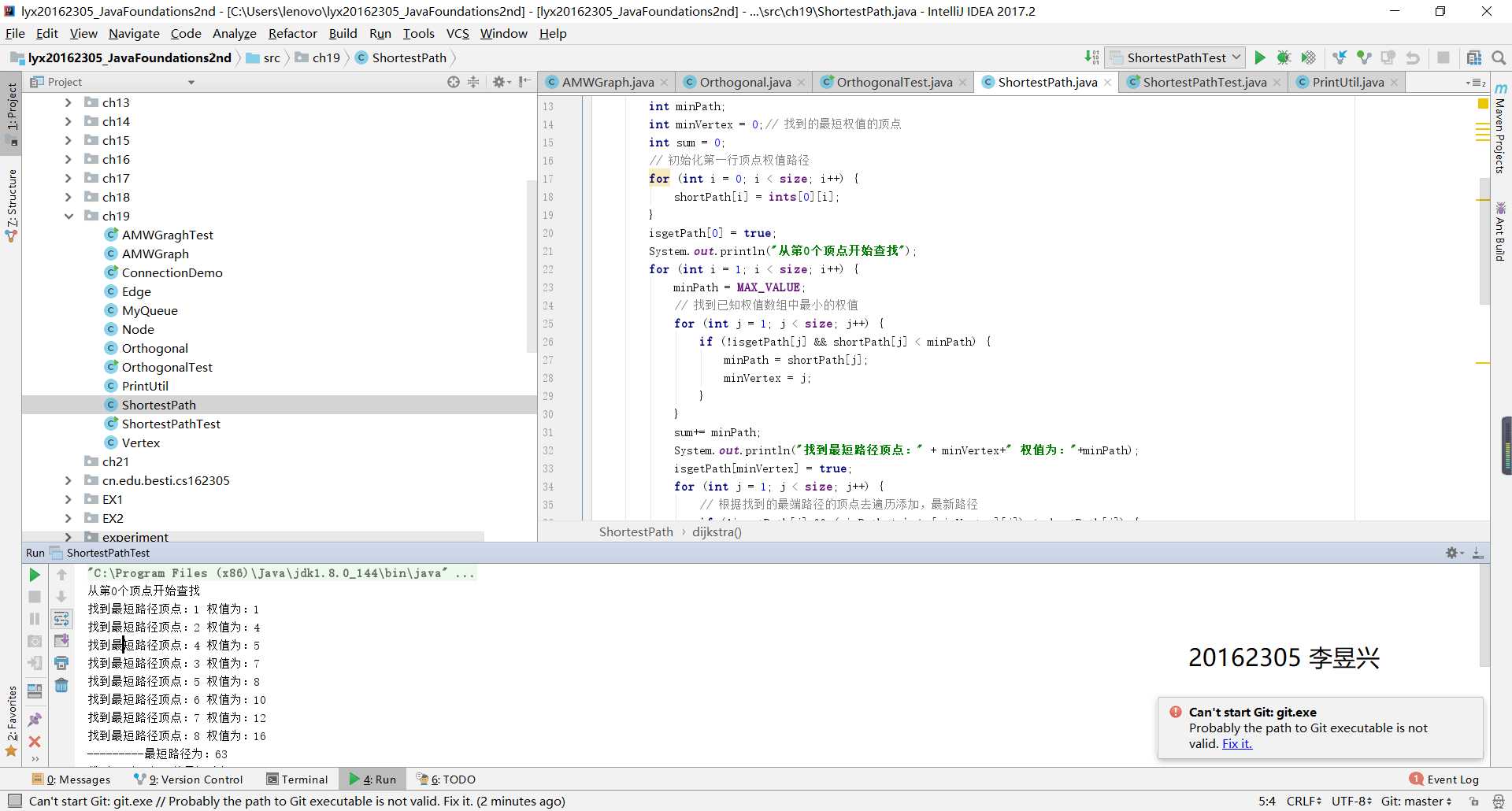
void dijkstra() {
        int[] shortPath = new int[size];
        boolean[] isgetPath = new boolean[size];
        int minPath;
        int minVertex = 0;// 找到的最短权值的顶点
        int sum = 0;
        // 初始化第一行顶点权值路径
        for (int i = 0; i < size; i++) {
            shortPath[i] = ints[0][i];
        }
        isgetPath[0] = true;
        System.out.println("从第0个顶点开始查找");
        for (int i = 1; i < size; i++) {
            minPath = MAX_VALUE;
            // 找到已知权值数组中最小的权值
            for (int j = 1; j < size; j++) {
                if (!isgetPath[j] && shortPath[j] < minPath) {
                    minPath = shortPath[j];
                    minVertex = j;
                }
            }
            sum+= minPath;
            System.out.println("找到最短路径顶点：" + minVertex+" 权值为："+minPath);
            isgetPath[minVertex] = true;
            for (int j = 1; j < size; j++) {
                // 根据找到的最端路径的顶点去遍历添加，最新路径
                if (!isgetPath[j] && (minPath + ints[minVertex][j]) < shortPath[j]) {
                    shortPath[j] = minPath + ints[minVertex][j];
                }
            }
        }

        System.out.println("---------最短路径为："+sum);
        for (int j = 1; j < size; j++) {
            System.out.println("找到V0到顶点V" + j + "的最短路径:"+shortPath[j]);
        }
    }

实验成果截图