题目描述
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你:蜜蜂从蜂房M开始爬到蜂房N,M<N,有多少种爬行路线?
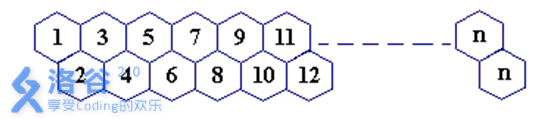
输入输出格式
输入格式:
输入M,N的值
输出格式:
爬行有多少种路线
输入输出样例
说明
对于100%的数据,M,N\le 1000M,N≤1000
思路:斐波那契。
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,m; struct nond{ int num[50000]; }f[1010]; void jia(int pos){ f[pos].num[0]=max(f[pos-1].num[0],f[pos-2].num[0]); for(int i=1;i<=f[pos].num[0];i++) f[pos].num[i]=f[pos-1].num[i]+f[pos-2].num[i]; for(int i=1;i<=f[pos].num[0];i++) if(f[pos].num[i]>=10){ if(i==f[pos].num[0]) f[pos].num[0]++; f[pos].num[i+1]+=1; f[pos].num[i]%=10; } for(;f[pos].num[0]>=1;f[pos].num[0]--) if(f[pos].num[f[pos].num[0]]) break; } int main(){ scanf("%d%d",&m,&n); n-=m; if(n==0){ cout<<"0";return 0;} f[1].num[1]=f[1].num[0]=f[0].num[0]=f[0].num[1]=1; for(int i=2;i<=n;i++) jia(i); for(int i=f[n].num[0];i>=1;i--) cout<<f[n].num[i]; }
