20162320刘先润大二实验四图及应用

时间：2017-11-26 19:38:30 阅读：202 评论：0 收藏：0 [点我收藏+]

标签：定义 mat .com length git let while 维度修改

实验涉及代码

AMatrix、AMatrixTest、CrossList、CrossListTest、Road、RoadTest

图的实现与应用-1

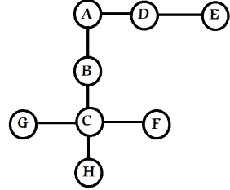
实验目的：用邻接矩阵实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器

实现思路：实现邻接矩阵得确定一个表示方法，对于结点于结点之间的关系得使用二元数组来实现。由于无向图的邻接矩阵是对称矩阵，且其左上角到右下角的对角线上值为零，这是其中应用的一条性质。所以根据实现步骤可以得出如下伪代码：

 确定图的顶点个数和边的个数； 
 输入顶点信息存储在一维数组vertex中；  
 初始化邻接矩阵； 
 依次输入每条边存储在邻接矩阵中；     
 输入边依附的两个顶点的序号i, j； 
 将邻接矩阵的第i行第j列的元素值置为1；   
 将邻接矩阵的第j行第i列的元素值置为1；

实验过程：

1.创建二位数组，并确定顶点和边的变量，得出size()和isEmpty()的方法，返回二维数组的大小和判定二维数组是否为空。
2.插入和删除边和结点,关于结点是输入点的名称，插入边则是输入边相连的两点的坐标确定其位置以及相应的权值。若删除边和结点，则是把两点的坐标修改为0和0，并将其对应的数目减一则删除成功。

 public void addVertex(Object vertex) {
        vertexList.add(vertexList.size(),vertex);
    }

 public void insertEdge(int v1,int v2,int weight) {
        edges[v1][v2]=weight;
        numOfEdges++;
    }
 public void deleteEdge(int v1,int v2) {
        edges[v1][v2]=0;
        numOfEdges--;
    }

3.得到下一个邻接结点的坐标,通过建立一个循环，查找到二维数组中索引维度下一个索引的位置，若越界则另一个索引维度加一得到返回值。

  public int getNextNeighbor(int v1,int v2) {
        for (int j=v2+1;j<vertexList.size();j++) {
            if (edges[v1][j]>0) {
                return j;
            }
        }
        return -1;
    }

4.广度遍历方法，过程是对每一层节点依次访问，访问完一层进入下一层，而且每个节点只能访问一次。对于上面的例子来说，广度优先遍历的结果是：A,B,C,D,E,F,G,H,I(假设每层节点从左到右访问)。首先私有函数广度遍历，创建一个队列保存结点，访问第i个结点并让其入队列.然后访问该结点，然后设置结点标记为已经被访问，然后入队列，并寻找下一个临接结点。

  private void broadFirstSearch(boolean[] isVisited, int i) {
        int a, b;
        LinkedList queue = new LinkedList();
        System.out.print(getValueByIndex(i) + "  ");
        isVisited[i] = true;
        queue.addLast(i);
        while (!queue.isEmpty()) {
            a = ((Integer) queue.removeFirst()).intValue();
            b = getFirstNeighbor(a);
            while (b != -1) {
                if (!isVisited[b]) {
                    System.out.print(getValueByIndex(b) + "  ");
                    isVisited[b] = true;
                    queue.addLast(b);
                }
                b = getNextNeighbor(a, b);
            }
        }
    }

    public void broadFirstSearch() {
        for(int i = 0; i< size(); i++) {
            if(!isVisited[i]) {
                broadFirstSearch(isVisited, i);
            }
        }
    }

5.深度优先遍历，对每一个可能的分支路径深入到最底层，并且每个节点只能访问一次。首先访问该结点并将其打印，然后将其设置为已访问状态，如果访问到结点为二维数组尽头则从没有遍历的结点访问，以此循环下去。

 public void depthFirstSearch(boolean[] isVisited,int  i) {
        System.out.print(getValueByIndex(i)+"  ");
        isVisited[i]=true;
        int w=getFirstNeighbor(i);//
        while (w!=-1) {
            if (!isVisited[w]) {
                depthFirstSearch(isVisited,w);
            }
            w=getNextNeighbor(i, w);
        }
    }

    public void depthFirstSearch() {
        for(int i = 0; i< size(); i++) {
            if (!isVisited[i]) {
                depthFirstSearch(isVisited,i);
            }
        }
    }

实验测试：创建如图所示的图进行测试

技术分享图片

图的实现与应用-2

实验目的：用十字链表实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器

实验思路：十字链表的结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。用链表模拟矩阵的行，然后再构造代表列的链表，将每一行中的元素节点插入到对应的列中去。

实验过程：

1.首先定义边和结点的类,提供一个输入方法，关于结点要设置先入先出，边则需要添加同入弧和同出弧变量，以方便指向。最后入结点和出结点指向对应的边，所以边链表需要有四个区域。

 public static class Vertex<E,T>  {
        E data;
        Edge<T> firstIn;
        Edge<T> firstOut;

        public Vertex(E data) {
            this.data = data;
        }
    }

    public static class Edge<E> {
        E data;
        int From;
        int To;
        Edge<E> SameFromVertex;
        Edge<E> SameToVertex;

 public Edge(E data, int From, int To) {
            this.data = data;
            this.From = From;
            this.To = To;
        }
    }

2.添加、删除边和点，首先创建两个收集集合与边的变量，用来统计二者的总数。添加点直接使用链表的添加方法并让结点总数加一即可，而删除点则需要不仅仅删除结点，还需要删除与此个结点相关的所有边的指向。添加边是需要将入结点插入到顶点或者插入到边的同入弧，如果该顶点没有入弧，则将结点指向为Null，最后添加边的总数。删除边则直接使用链表的remove方法即可。

  public void removeV(Vertex<Integer, Integer> vex){
        for (int index = 0; index< AllEdge.size(); index++){
            if (AllEdge.get(index).From== AllVertex.indexOf(vex)|| AllEdge.get(index).To== AllVertex.indexOf(vex)){
                AllEdge.remove(index);
                index=0;
            }
        }
        AllVertex.remove(vex);
    }

 public void addE(Edge<Integer> edge) {
        Edge<Integer> edge1 = new Edge<>(edge.data,edge.From,edge.To);
        Edge<Integer> edge2 = new Edge<>(edge.data,edge.From,edge.To);
        AllEdge.add(edge);
        int fromVertexIndex = edge.From;
        int toVertexIndex = edge.To;
        Vertex<Integer, Integer> fromVertex = AllVertex.get(fromVertexIndex);
        Vertex<Integer, Integer> toVertex = AllVertex.get(toVertexIndex);
        if (fromVertex.firstOut == null) {
            fromVertex.firstOut = edge1;
        } else {
            Edge<Integer> tempEdge = fromVertex.firstOut;
            while (tempEdge.SameFromVertex != null) {
                tempEdge = tempEdge.SameFromVertex;
                System.out.println();
            }
            tempEdge.SameFromVertex = edge1;
        }
        if (toVertex.firstIn == null) {
            toVertex.firstIn = edge2;
        } else {
            Edge<Integer> tempEdge = toVertex.firstIn;
            while (tempEdge.SameToVertex != null) {
                tempEdge = tempEdge.SameToVertex;
            }
            tempEdge.SameToVertex = edge2;
        }
        System.out.println();
    }

3.添加size()方法需要将添加的结点保存至一个集合，否则无法得到返回值。

 static List<Vertex<Integer,Integer>> AllVertex = new ArrayList<>();
public int size(){
        return AllVertex.size();
    }

4.广度以及深度遍历，深度遍历实现方法：首先选择一个顶点入栈，如果栈非空栈，则出栈并访问出栈元素，并标示为已访问。然后将出栈顶点的邻接顶点（要求未被访问过）全部入栈。重复前一步骤直至没有可以访问到的顶点。广度遍历方法：首先选择一个未被访问的顶点入队。如果队列非空队列，则出队并访问，然后标记为已被访问。并将出队顶点的邻接顶点都入队。然后重复前一个步骤直至没有可以访问的顶点。（详细代码见代码连接）

实验测试：创建一个测试图进行测试，如图所示

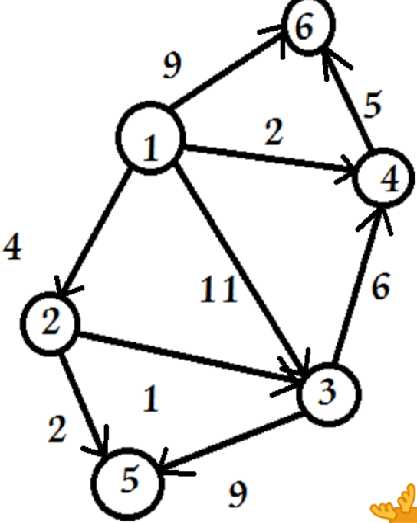
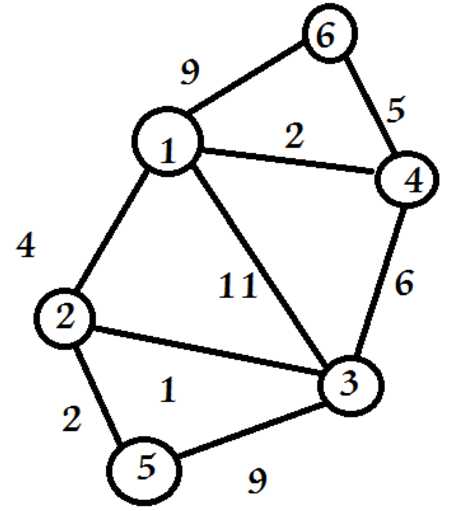
技术分享图片

图的实现与应用-3

实验目的：创建计算机网络路由系统，输入网络中点到点的线路，以及每条线路使用的费用，系统输出网络中各点之间最便宜的路径，指出不相通的所有位置。

实验思路：该实验需要求出最短路径，可以通过求单源最短路径，使用Dijkstra算法。

实验过程：

1.创建无向图的变量表示，存储所有顶点的一维数组，存储图中顶点与边关系的二维数组，对数组进行初始化，顶点间没有边关联的值为int类型最大值

    public Road(boolean graphType, boolean method, int size) {
        this.graphType = graphType;
        this.method = method;
        this.NumVertex = 0;
        this.matrix = size;

        if (this.method) {
            visited = new boolean[matrix];
            vertexesArr = new Object[matrix];
            edgesMatrix = new int[matrix][matrix];

            for (int row = 0; row < edgesMatrix.length; row++) {
                for (int column = 0; column < edgesMatrix.length; column++) {
                    edgesMatrix[row][column] = MAX_VALUE;
                    System.out.print("");
                }
            }
        }
    }

2.求单个点到其他点的最便宜路径长度，即求最小权值路径。可以一开始假设直达路径为最短路径，在这种情况下的最后经由点就是出发点。初始数组时起点v0访问集合，表示v0 到v0的最短路径已经找到
。然后下来假设经由一个点中转到达其余各点,会权值更小近些并验证之，然后重复该过程，直到列举完所有可能的点。创建一个循环将最短路径的权值记录并且打印出来。

public void Dijkstra(int v0) {
        int[] dist = new int[matrix];
        int[] prev = new int[matrix];

        for (int i = 0; i < NumVertex; i++) {
            dist[i] = edgesMatrix[v0][i];
            visited[i] = false;
            if (i != v0 && dist[i] < MAX_VALUE)
                prev[i] = v0;
            else
                prev[i] = -1;
        }

        visited[v0] = true;
        int minDist;
        int v = 0;
        for (int i = 1; i < NumVertex; i++) {
            minDist = MAX_VALUE;

            for (int j = 0; j < NumVertex; j++) {
                if ((!visited[j]) && dist[j] < minDist) {
                    v = j;
                    minDist = dist[j];
                }
            }
            visited[v] = true;

            for (int j = 0; j < NumVertex; j++) {
                if ((!visited[j]) && edgesMatrix[v][j] < MAX_VALUE) {
                    if (minDist + edgesMatrix[v][j] <= dist[j]) {
                        dist[j] = minDist + edgesMatrix[v][j];
                        prev[j] = v;
                    }

                }
            }

        }

        for (int i = 0; i < matrix; i++) {
            if (dist[i] > 1000) {
                dist[i] = 0;
            }
            System.out.println(vertexesArr[v0] + "到" + vertexesArr[i] + "的最短路径是：" + dist[i]);
        }
    }

3.求出最短的路径可以使用Dijkstra算法。创建一个队列，通过步骤2求出最便宜权值的路径方法记录其经过并且标记的结点，将其输出出去，并且访问未标记的结点得到Dijkstra算法的最短路径。

 public void DRoad(int v0) {
        Queue<Integer> queue = new LinkedList<Integer>();
        for (int i = 0; i < NumVertex; i++) {
            visited[i] = false;
        }

        for (int i = 0; i < NumVertex; i++) {
            if (!visited[i]) {
                queue.add(i);
                visited[i] = true;
                while (!queue.isEmpty()) {
                    int row = queue.remove();
                    System.out.print(vertexesArr[row] + "→");
                    for (int k = getMin(row); k >= 0; k = getMin(row)) {
                        if (!visited[k]) {
                            queue.add(k);
                            visited[k] = true;
                        }
                    }
                }
            }
        }
    }