标签:伪代码 删除 下标越界 logs div 很多 personal 成功 十字链表
课程名称:《程序设计与数据结构》
学生班级:1623班
学生姓名:刘伟康
学生学号:20162330
实验时间:2017年11月20日—2017年11月24日
实验名称:图的实现与应用
指导老师:娄嘉鹏、王志强老师
1.用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器。
给出伪代码,产品代码,测试代码(不少于5条测试);
2.用十字链表实现有向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器。
给出伪代码,产品代码,测试代码(不少于5条测试);
3.实现PP19.9。
给出伪代码,产品代码,测试代码(不少于5条测试)。
图的实现与应用-1:【方法类】及【测试类】
图的实现与应用-2:【方法类】及【测试类】
图的实现与应用-3:【方法类】及【测试类】
用邻接矩阵实现无向图:
(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器。
关于邻接矩阵实现无向图中边和顶点的存储策略,可以将图的顶点用一个一维数组存放,将图的边用一个二维数组存放,其中这个边集合就相当于邻接矩阵了:
private Object[] vexs; //顶点集合
private int[][] arcs; //边集合,邻接矩阵另外我设定了顶点数目和边数目,其中我将顶点数目定义为决定图的大小的变量:
private int gSize, arcNum; //顶点数目、边数目于是,判断一个图是否为空的 isEmpty() 方法和返回图的大小的 size() 方法就可以根据顶点数目定义了:
//判断图的大小(顶点个数)
public int size() {
return gSize;
}
//判断图是否为空
public boolean isEmpty() {
return gSize == 0;
}关于添加一条边和删除一条边我还没有考虑那么多种情况(还会补充),所以只实现了基本的功能,即邻接矩阵对角线上对应的两边数值添加时都变为1,删除时都变为0:
//添加一条边
public void addArc(int x, int y) {
arcs[x][y] = 1;
arcs[y][x] = 1;
arcNum++;
}
//删除一条边
public void removeArc(int x, int y) {
arcs[x][y] = 0;
arcs[y][x] = 0;
arcNum--;
}关于添加和删除顶点,我参考了网上的一些思路,然而还没有测试成功,所以这部分内容待补充,实现代码如下:
//添加一个顶点
public void addVex() {
for (int i = 0; i < gSize; i++) {
arcs[i][gSize] = INFINITY;
}
for (int i = 0; i < gSize; i++) {
arcs[gSize][i] = INFINITY;
}
arcs[gSize][gSize] = 0;
gSize++;
System.out.println("Insert successfully.");
}
//删除一个顶点
public void removeVex(int v) {
if (v >= gSize) {
System.out.println("The graph doesn't have this vertex.");
}
for (int i = 0; i < gSize; i++) {
arcs[v][i] = 0;
arcs[v][i] = 0;
}
if (v == gSize - 1) {
gSize--;
}
for (int i = v + 1; i < gSize; i++) {
for (int j = 0; j < gSize; j++) {
arcs[i - 1][j] = arcs[i][j];
}
}
gSize--;
}之后来说说图的遍历方法的实现,首先常见的图的遍历方法有两种:① 广度优先遍历;② 深度优先遍历。(代码就先不贴出来了)
对于广度优先遍历,先访问某个顶点,再依次访问每一个未被访问过的邻接点,然后按照这个顺序访问其他顶点,之后访问各个还未被访问过的邻接点,以此类推,直到所有顶点都被访问过为止,可以参考下图:
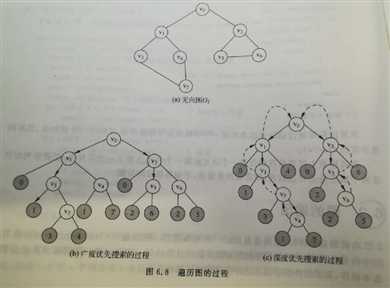
使用队列实现广度优先遍历的具体思路如下:
(1)顶点v入队列。
(2)当队列非空时则继续执行,否则算法结束。
(3)出队列取得队头顶点v;访问顶点v并标记顶点v已被访问。
(4)查找顶点v的第一个邻接顶点w。
(5)若v的邻接顶点w未被访问过的,则w入队列。
(6)继续查找顶点v的另一个新的邻接顶点w,转到步骤(5)。
直到顶点 v 的所有未被访问过的邻接点处理完。转到步骤(2)。
实现广度优先遍历的关键就在于要设立一个访问标志数组,初值为0,某顶点被访问后,相应下标元素置为1。
对于深度优先遍历,先从图的某个顶点 v 开始访问,然后访问它的任意一个邻接点w1,再从w1出发,访问与w1邻接但未被访问的顶点w2,然后从w2出发,依次访问,直至所有的邻接点被访问过。之后,退到前一次访问过的顶点,看是否还有其他未被访问过的邻接点。如果有,则访问此顶点,没有再退到前一次访问过的顶点,重复这一过程,直到所有顶点都被访问过为止。(递归)
使用队列实现深度优先遍历的具体思路如下:
(1)输入要访问的结点Vi;
(2)访问顶点vi;visited[vi]=1;
(3)在邻接矩阵的第i行中查找,若vi有邻接点vj,且vj未被访问过,则设 i=j;
(4)重复步骤1至3,直到所有结点均被访问到。
和广度优先遍历相同的是,深度优先遍历也要设立一个访问标志数组visited[N],初值为0,某点被访问,则相应下标变量置为1。
在测试时,我直接使用了根据输入的边和顶点创建邻接矩阵的方法,测试运行截图如下:(部分)
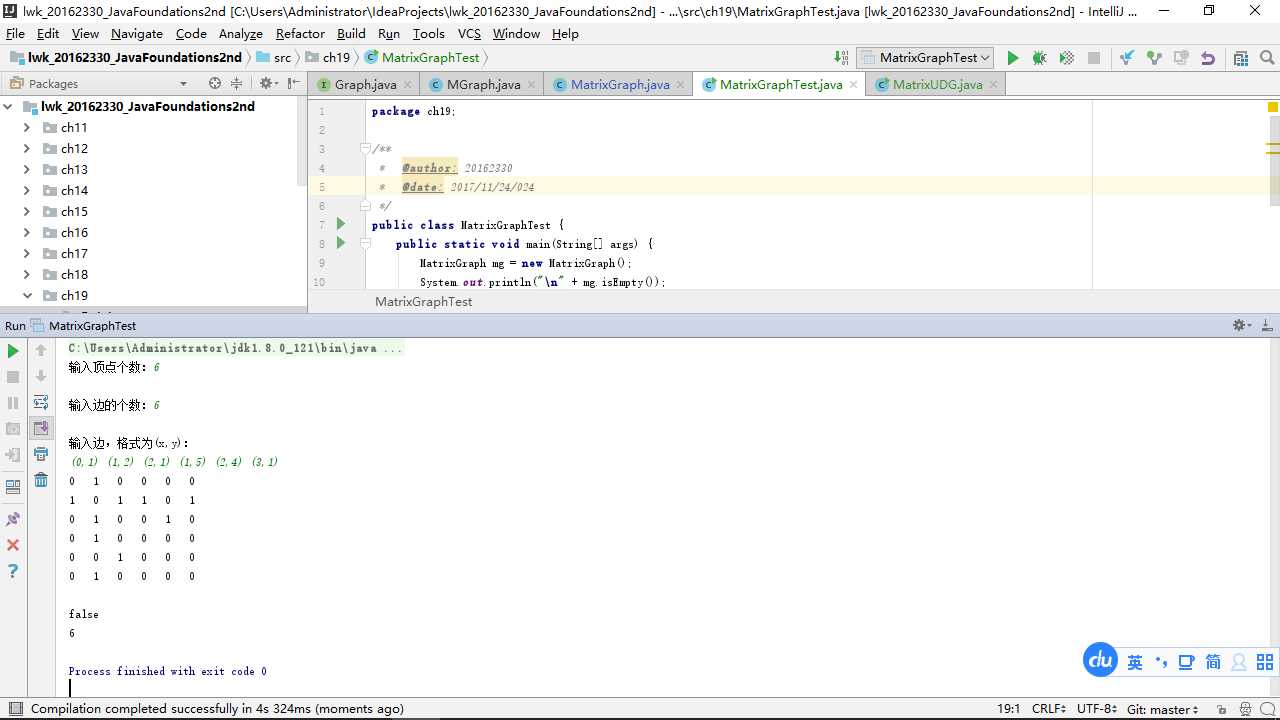
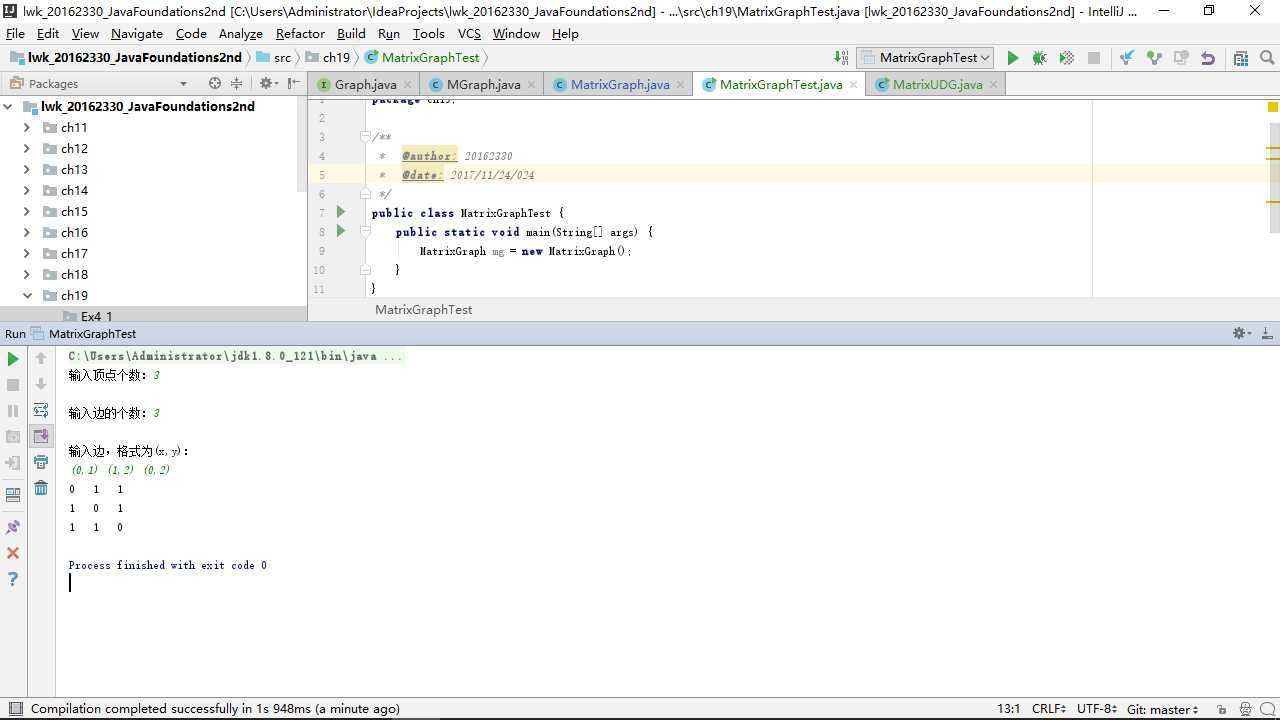
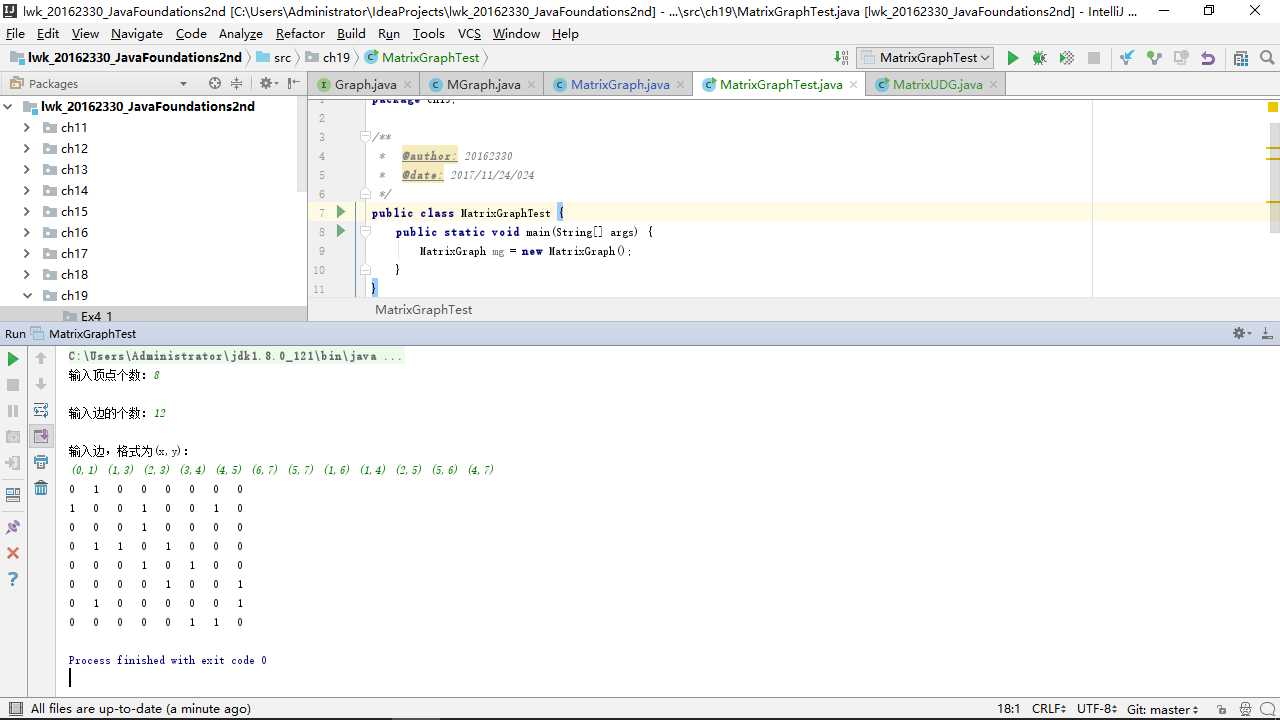
用十字链表实现有向图:
(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器。
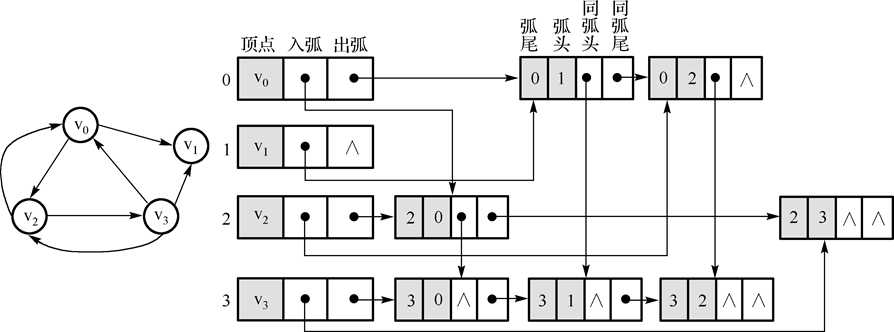
实现这个就有点难了,原因是十字链表是针对有向图的,这需要考虑到所有边对应的权值,我参考了网上相关资料的代码,关于顶点和边,可以单独定义两个类:
在定义十字链表的边的类时,要设定入弧顶点和出弧顶点两个形参:
public class CrossEdge<E> {
E data;
int fromVertexIndex;
int toVertexIndex;
CrossEdge<E> nextSameFromVertex;
CrossEdge<E> nextSameToVertex;
public CrossEdge(E data, int fromVertexIndex, int toVertexIndex) {
this.data = data;
this.fromVertexIndex = fromVertexIndex;
this.toVertexIndex = toVertexIndex;
}
}在定义十字链表的顶点的类时,需要定义顶点的data形参:
public class CrossVertex<E, T> {
E data;
CrossEdge<T> firstIn;
CrossEdge<T> firstOut;
public CrossVertex(E data) {
this.data = data;
}
}我还没太搞懂方法类中的代码,方法类中的设计思路之后会有补充。
测试运行截图如下:
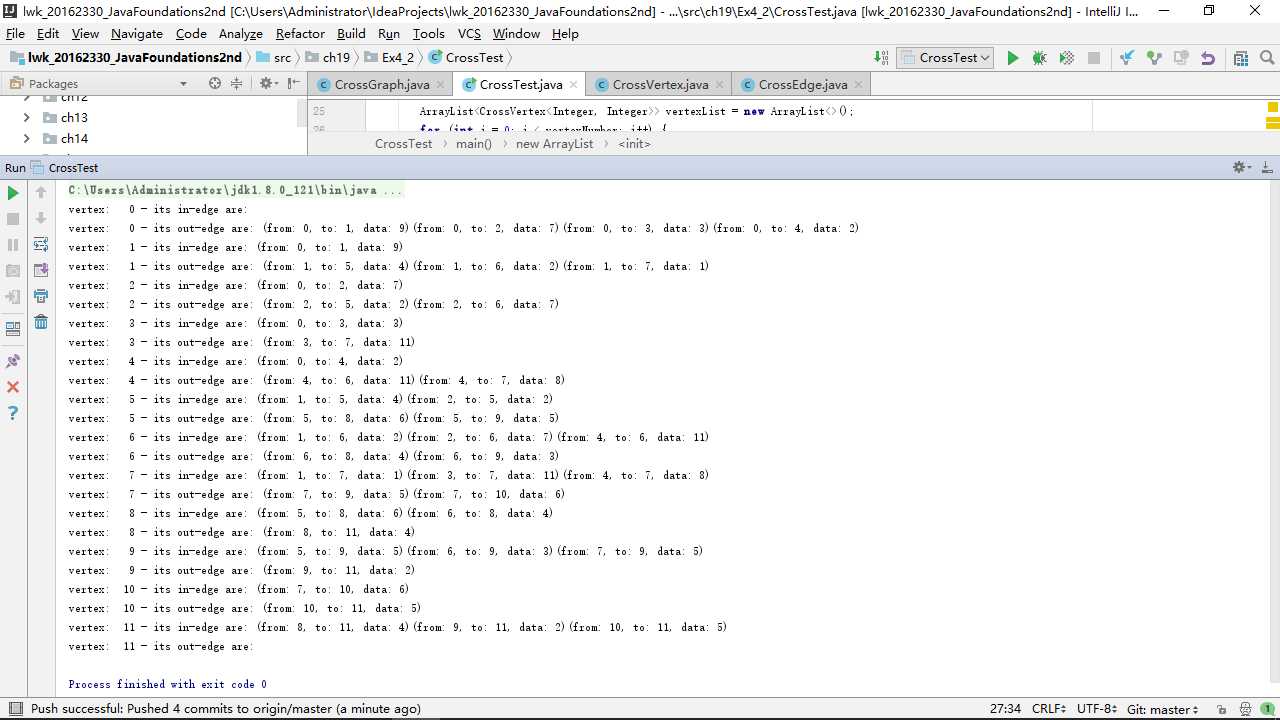
实现PP19.9(最短路径)。
对于如何解决有向图中顶点间的最短路径问题,我在这里使用了戴克斯特拉算法,具体实现如下:
public void DIJ(MGraph G, int v0){
int vexNum = G.getVexNum(); // 顶点数
this.P = new boolean[vexNum][vexNum];
this.D = new int[vexNum];
//finish[v]为true当且仅当v属于S,即已经求得从v0到v的最短路径
boolean[] finish = new boolean[vexNum];
//初始化所有数据
for(int v = 0; v < vexNum; v++){
finish[v] = false;
D[v] = G.getArcs()[v0][v];
for(int w = 0; w < vexNum; w++){
P[v][w] = false;
}
if(D[v] < INFINITY){
P[v][v0] = true;
P[v][v] = true;
}
}
D[v0] = 0; //从v0开始,并入S集
finish[v0] = true;
int v = -1 ;
//开始主循环,每次求得v0到某个v顶点的最短路径,并将v加入到S集.循环n-1次
for(int i = 1; i < vexNum; i++){
int min = INFINITY; //当前所知离v0最近的距离
for(int w = 0; w < vexNum; w++){
if( !finish[w]){
if(D[w] < min){
v = w;
min = D[w];
}
}
}
finish[v] = true; //离v0最近的v并入S
//更新当前最短路径和距离
for(int w = 0; w < vexNum; w++){
if( !finish[w] && G.getArcs()[v][w] < INFINITY && (min + G.getArcs()[v][w] < D[w])){
D[w] = min + G.getArcs()[v][w];
//下面两句这么理解,现在路径是v0-v-w,所以经过了v点,那么v0到v的最小路径自然要给w,同时再加上w点(P[W][W] = true)
System.arraycopy(P[v], 0, P[w], 0, P[v].length);
P[w][w] = true;
}
}
}
}测试运行截图如下:(其中,vo表示网络中的点,分别计算vo到各个结点的最短路径)
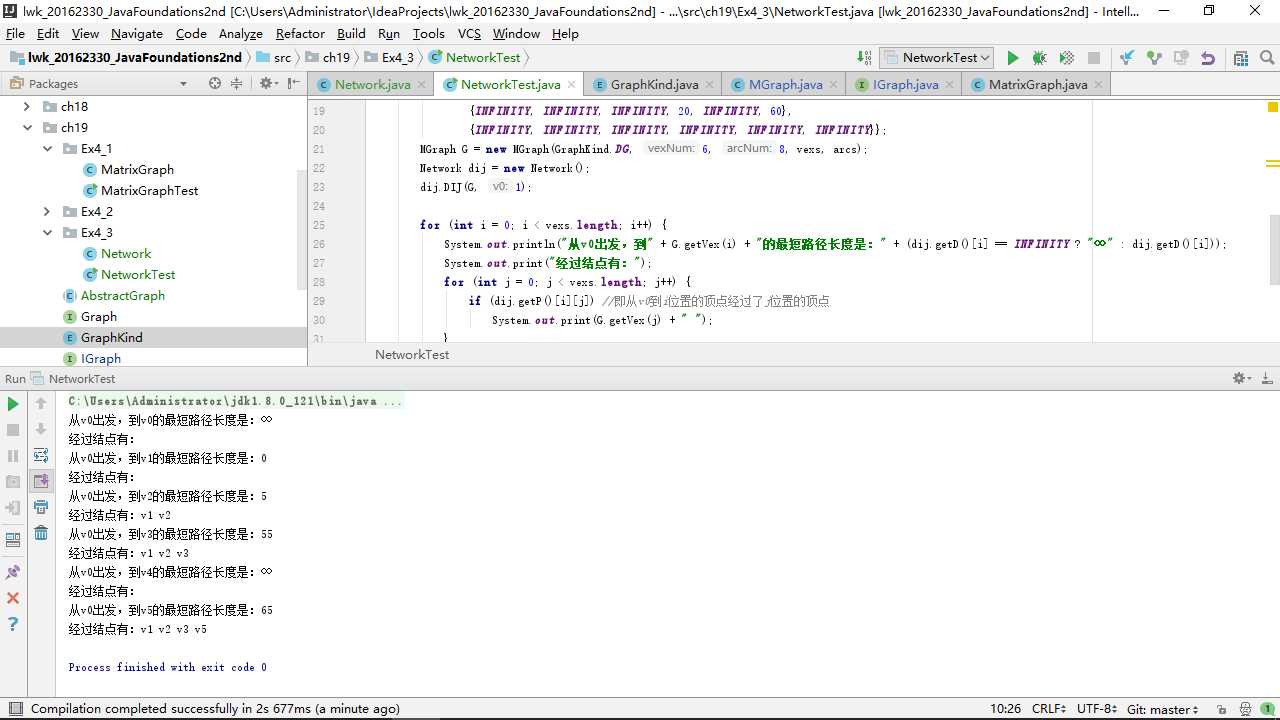
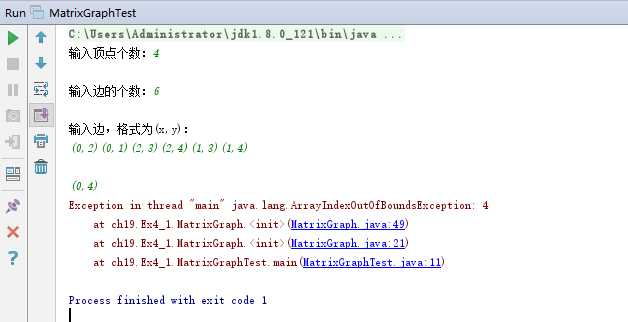
解决办法:(使用debug单步跟踪进行调试)
调试之后我发现是我的输入格式出了问题,各个边之间是要加一个空格的,因为我在调用了 Scanner 中的 next 方法依次检测输入的边,而在各个边的间隔之间,是要留出一个空格的距离的:
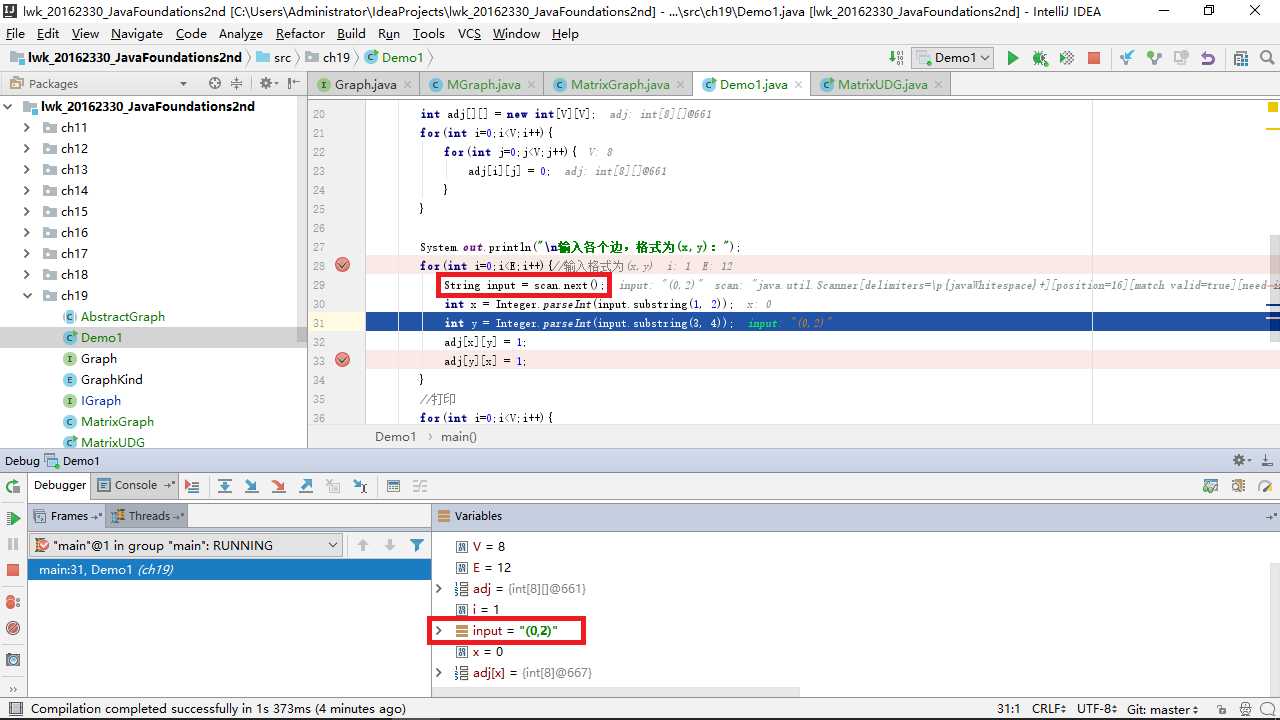
知道了这一“特定格式”之后,再运行时就没有出错了。
| 步骤 | 耗时 | 百分比 |
|---|---|---|
| 需求分析 | 60min | 15% |
| 设计 | 60min | 15% |
| 代码实现 | 120min | 30% |
| 测试 | 80min | 20% |
| 分析总结 | 80min | 20% |
2017-2018-1 20162330 实验四 图的实现与应用
标签:伪代码 删除 下标越界 logs div 很多 personal 成功 十字链表
原文地址:http://www.cnblogs.com/super925/p/7898141.html