标签:batch 时报 枚举 输出 激活 pac status 物理学 构造
http://blog.csdn.net/omnispace/article/details/78061776
这有可能也是知乎上面分析介绍深度学习最为全面的文章之一。希望做物理的,做数学的,做生物的,做化学的,做计算机,包括做科幻的都能看的很开心。
Hinton 以“深度学习之父” 和 “神经网络先驱” 闻名于世,其对深度学习及神经网络的诸多核心算法和结构(包括“深度学习”这个名称本身,反向传播算法,受限玻尔兹曼机,深度置信网络,对比散度算法,ReLU激活单元,Dropout防止过拟合,以及深度学习早期在语音方面突破)做出了基础性的贡献。尽管已经将大半辈子的时间投入到神经网络之上,这位老人却丝毫没有想退休的意思。
Hinton 近几年以 “卷积神经网络有什么问题?” 为主题做了多场报道 [1] [2],提出了他的 Capsule 计划。Hinton似乎毫不掩饰要推翻自己盼了30多年时间才建立起来的深度学习帝国的想法 [3]。他的这种精神也获得了同行李飞飞(ImageNet创始者)等人肯定 [4]。
Hinton 为什么突然想要推倒重来?这肯定不是出于巧合或者突然心血来潮,毕竟作为一个领域的先驱,质疑自己亲手建立的理论,不是谁都愿意做的事情。(试想一下,如果你到处做报告,说自己的领域有各种各样的问题,就算不会影响到自己,也让做这个领域的同行和靠这个领域吃饭的人不是很舒服)
说推倒重来有点过分,Hinton并没有否定一切,并且他的主要攻击目标是深度学习在计算机视觉方面的理论。但是从几次演讲来看,他的 Capsule 计划确实和以前的方法出入比较大。Hinton 演讲比较风趣,但是也存在思维跳跃,难度跨度太大等问题。这些问题在他的关于 Capsule 的报告中还是比较突出的。可以说仅仅看报告很难理解完全 Hinton 的想法。我这几天结合各类资料,整理了一下 Hinton 的思路和动机,和大家分享一下。
(以下用NN指代人工神经网络,CNN指代(深度)卷积神经网络,DNN指代深度神经网络)
要深入理解Hinton的想法,就必须了解神经网络发展的历史,这也几乎是Hinton的学术史。
人工智能才起步的时候,科学家们很自然的会有模拟人脑的想法(被称为连接主义),因为人脑是我们唯一知道的拥有高级智能的实体。
NN 起源于对神经系统的模拟,最早的形式是感知机,学习方法是神经学习理论中著名的 Hebb‘s rule 。NN最初提出就成为了人工智能火热的研究方向。不过 Hebb‘s rule 只能训练单层NN,而单层NN甚至连简单的“异或”逻辑都不能学会,而多层神经网络的训练仍然看不到希望,这导致了NN的第一个冬天。
Hinton 意识到,人工神经网络不必非要按照生物的路子走。在上世纪80年代, Hinton 和 LeCun 奠定和推广了可以用来训练多层神经网络的反向传播算法(back-propagation)。NN再次迎来了春天。
反向传播算法,说白了就是一套快速求目标函数梯度的算法。
对于最基本的梯度下降(Gradient Descent):
,反向传播就是一种高效计算
的方式
不过在那时,NN就埋下了祸根。
首先是,反向传播算法在生物学上很难成立,很难相信神经系统能够自动形成与正向传播对应的反向传播结构(这需要精准地求导数,对矩阵转置,利用链式法则,并且解剖学上从来也没有发现这样的系统存在的证据)。反向传播算法更像是仅仅为了训练多层NN而发展的算法。失去了生物学支持的NN无疑少了很多底气,一旦遇到问题,人们完全有更多理由抛弃它(历史上上也是如此)
其次是,反向传播算法需要SGD等方式进行优化,这是个高度非凸的问题,其数学性质是堪忧的,而且依赖精细调参。相比之下,(当时的)后起之秀SVM等等使用了凸优化技术,这些都是让人们远离NN的拉力。当那时候的人们认为DNN的训练没有希望(当时反向传播只能训练浅层网络)的时候,NN再次走向低谷。
第二次NN低谷期间,Hinton没有放弃,转而点了另外一个科技树:热力学统计模型。
Hinton由玻尔兹曼统计相关的知识,结合马尔科夫随机场等图学习理论,为神经网络找到了一个新的模型:玻尔兹曼机(BM)。Hinton用能量函数来描述NN的一些特性,期望这样可以带来更多的统计学支持。
不久Hinton发现,多层神经网络可以被描述为玻尔兹曼机的一种特例——受限玻尔兹曼机(RBM)。Hinton 在 Andrew Ng 近期对他的采访中 (https://www.youtube.com/watch?v=-eyhCTvrEtE),称其为 "most beautiful work I did"。
当年我第一次看到 RBM 的相关数学理论的时候,真的非常激动,觉得这样的理论不work有点说不过去。这里我给出相关的数学公式,以展示NN可以有完全不同于生物的诠释方式。
在统计力学中,玻尔兹曼分布(或称吉布斯分布)可以用来描述量子体系的量子态的分布,有着以下的形式:
其中 s 是某个量子态, 为这个状态的能量,
为这个状态出现的概率。
k是玻尔兹曼常量,是个常数。T是系统温度,在具体问题中也是一个常数。于是我们不妨让kT=1,原来的表达式可以简化为
也就是
这不就是 softmax 吗?居然自然地在统计力学分布里面出现了(难怪之前 LeCun 让大家学物理)。
为了再次简化,我们定义 ,于是就有
,(因为这时候公式里面只有一个s,就没有必要写下标了)
下面问题来了, 是什么?
又应该是什么?
Hinton 看了看神经网络的一层,其分为可见层(输入层)和隐含层(中间层)。按照经典网络的定义,神经元有激活和未激活两个状态。那么干脆让 等于可见层
并上隐含层
神经元的状态吧(默认都用向量的方式表示):
于是 ,
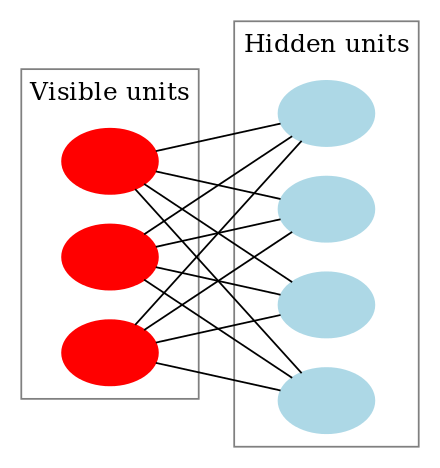
那么 又是什么呢?
非常巧合的是,量子物理学里面有个模型极其像神经网络,以至于只要了解过几乎都会惊叹两者的相似度。这个模型就是著名 易辛模型(Ising model)。易辛模型(物理学界常见调侃:你3维 Ising 模型会解了吗?)描述了晶格系统中的相变,解释了铁磁性问题(你可能好奇过,为啥这么多金属,就铁等少数金属特别敏感,而且还能被磁化。这个模型给出了解释)。
Hinton 把神经元的偏置(对于可见层记作 ,对于隐含层记作
) 作为 Ising model 的 “外场”,NN的权重
作为 Ising Model 的“内部耦合系数”(两个神经元之间的权重越大,代表它们的耦合越强,关联越强),于是能量就可以写作非常简单的形式:
这个形式让人惊讶之处在于,在没有浪费任何一个NN中的参量的情况下做到了最简,并且非常合理的直觉:神经元的偏置只和神经元本身通过乘法直接相关,而两个神经元间的权重也只和对应的两个神经元通过乘法直接相关,而整体的贡献用加法联系起来。
我们可以将某个神经元 关联的能量分离出来,也就是
,其中
是和神经元
相连的权重,
是除去
的向量。
为了方便,我们把和 无关的部分记作
于是,
于是很容易得到
这不就是sigmoid函数吗?也就是
这时候 sigmoid 函数就有了自然的解释:玻尔兹曼分布下隐含层神经元激活的条件概率的激活函数。
如果你是 Hinton,推导到这一步,肯定也会觉得是个喜出望外的结果吧。
而优化的目标,就是极大似然估计,也就是最大化
,这里其实也非常有趣,因为和热力学统计中的自由能非常相关。
定义自由能为 (“自由”可以理解为
拥有额外的自由度,其蕴含的能量在体系中可以用来对外做功),则
于是有 ,即
是关于自由能的玻尔兹曼分布。也就是我们找的参数是使得出现的样本的自由能(在参数约束的分布中)最低的一组参数。这样参数选择就和样本分布通过最低能量联系起来。
总之一切看上去都很有道理。Hinton展现了NN和玻尔兹曼分布间惊人的联系(其在论文中多次称 surprisingly simple [7]),其背后的内涵引人遐想。甚至有人在听过Hinton的讲座之后,还发现RBM的训练模式和量子重整化群的重整化步骤是同构的 [6]。
不过问题是,优化整体网络是困难的,其根源性被认为在于配分函数 。求得最低能量对应的结构一般意义上是个
的问题,如果真的能够有有效算法,那么很多热力学系统,包括 Ising 模型也就迎刃而解。
Hinton 使用贪心的方式来降低算法复杂度:逐层训练网络,而不是整体优化。而为了训练每层RBM,Hinton发展了所谓的对比散度(contrastive divergence)算法。
CD算法利用了 Gibbs sampling,但是算法收敛的非常慢(这已经是贪心处理过的问题了,可见原问题多难)。Hinton再次近似,固定采样步数 ,被称为
算法。Hinton 惊奇的发现
的时候(显然是极度粗糙的近似),算法的表现就已经相当良好了。
Hinton 发现用这个粗糙的算法预训练网络(这个时候是无监督学习,也就是只需要数据,不需要标签;在下面会提到)后,就可以通过调优(加上标签,使用反向传播继续训练,或者干脆直接在后面接个新的分类器)高效且稳定地训练深层神经网络。
之后“深度学习”这个词逐渐走上历史的前台,虽然 1986年就有这个概念了 [8]。可以说 RBM 是这一波人工智能浪潮的先行者。
这让人想起了另外一个相当粗糙但是甚至更加成功的算法——SGD。可以说,利用梯度的算法 中很难有比SGD还简单的了,但是SGD(加上动量后)效果确实特别好。非常粗糙的算法为何却对NN的优化这种非常复杂的问题很有效,这也是一个非常有趣的开放问题。
由于玻尔兹曼机本身的特性,其可以被用来解决“无监督学习”(Unsupervised learning)相关的问题。即使没有标签,网络也可以自己学会一些良好的表示,比如下面是MNIST的:
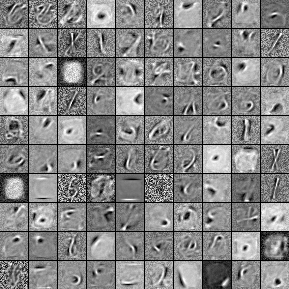
当我们将人类智能,和目前的人工智障对比时,常常举的例子就是“现在机器学习依赖大数据,而人类的学习却是相反的,依赖小数据”。这个说法其实不尽准确。人类拥有太多的感知器官,无时无刻不接收着巨量的数据:就按人眼的分辨率而言,目前几乎没有什么实际的机器学习模型模型使用如此高清晰度的数据进行训练的。我们观察一个东西的时候,所有的知觉都潜移默化地给我们灌输海量的数据,供我们学习,推理,判断。我们所谓的“小数据”,实际上主要分为两个部分:
不过不久,人们发现,使用ReLU以及合适的初始化方法,用上CNN,搭配上强劲的GPU之后,发现原来的深度神经网络可以照常训练,根本不用RBM预训练。RBM虽然数学上很漂亮,但是受结构限制严重,而且在supervised learning方面往往搞不过直接暴力反向传播。前几年Andrew Y. Ng在Google让神经网络自动检测视频中的猫的时候,Google内部的深度学习框架几乎就是用来支持RBM等的训练的。而现在Google开源的TensorFlow等主流框架中都没有RBM的影子。很多从TensorFlow入手的新人估计也没有听过RBM。
好了,现在除了各种小修小改(残差网络,Adam优化器,ReLU,Batchnorm,Dropout,GRU,和稍微创意点的GAN),神经网络训练主流算法又回到了30年前(那个时候CNN,LSTM已经有了)的反向传播了。
目前来看,很多对 NN 的贡献(特别是核心的贡献),都在于NN的梯度流上,比如
说到底,相对于8,90年代(已经有了CNN,LSTM,以及反向传播算法),没有特别本质的改变。
但是为什么当前这种方式实际效果很好?我想主要有:
不过 Hinton 看上去是不会对目前这种结果满意的。他在2011年的时候,就第一次提出了Capsule 结构[9](我们会在后面解释Capsule是什么)。不过那次Hinton打擂显然没有成功。
Hinton最近抓住了NN中最成功的CNN批判了一番,又重新提出了Capsule 结构。可以明确的是,Hinton 受到了下面3个领域的启示:
其中前两者明显是和人脑相关的。可能不少读者都有疑问:NN非要按照生物的路子走吗?
回答是:看情况。
对于人脑中存在的结构和现象,可以从不同的观点看待:
不过首先的一个问题是,我们怎么知道某个人脑的功能或者结构属于上面的第3点呢?按照上面的观点,显然生物的某个结构和功能本身的出现不能说明它很有用。我们需要更多证据。
一个重要的统计学证据是普遍性。我们为什么会有拿NN做AI的想法?因为NN本身正是生物进化中的重大突破,凡是有NN的生物中,我们都发现NN对其行为调控起了关键性作用,尤其是人类。这也是我们如今愿意相信它的理由,而不只是因为人有一个大脑,所以我们就必须搞一个(就像我们不给AI做肝脏一样)。
人的实际神经系统是有分层的(比如视觉系统有V1, V2等等分层),但是层数不可能像现在的大型神经网络(特别是ResNet之后)一样动不动就成百上千层(而且生物学上也不支持如此,神经传导速度很慢,不像用GPU计算神经网络一层可能在微秒量级,生物系统传导一次一般在ms量级,这么多层数不可能支持我们现在这样的反应速度,并且同步也存在问题)。
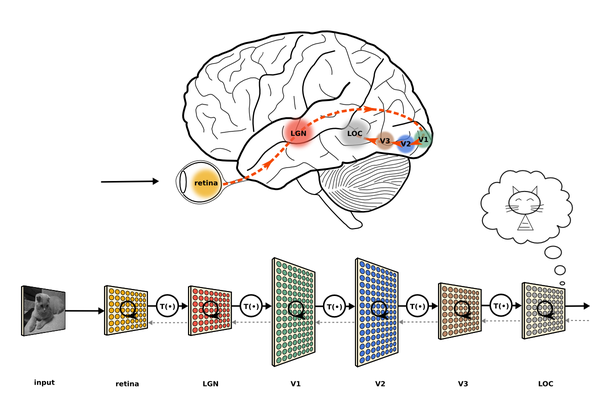
(将人脑视觉通路分层和DNN分层的类比。Image (c) Jonas Kubilias)
Hinton 注意到的一个有趣的事实是,目前大多数神经解剖学研究都支持(大部分哺乳类,特别是灵长类)大脑皮层中大量存在称为 Cortical minicolumn 的柱状结构(皮层微柱),其内部含有上百个神经元,并存在内部分层。这意味着人脑中的一层并不是类似现在NN的一层,而是有复杂的内部结构。

(mini-column 图片,引自 minicolumn hypothesis in neuroscience | Brain | Oxford Academic)
为什么大脑皮层中普遍存在 mini-column?这显然是一个重要的统计学证据,让 Hinton 愿意相信 mini-column 肯定起了什么作用。于是 Hinton 也提出了一个对应的结构,称为 capsule (胶囊,和微柱对应)。这就是 capsule 的由来。
但是 capsule 做了什么?之前的CNN又有什么问题?统计学证据不能给出这些的答案。Hinton的这部分答案来自认知神经科学。
每一个机器学习的初学者都应该了解关于机器学习的重要定律——“没有免费的午餐”[10]
这个可以通过科幻小说《三体》里面的提到一个例子来理解:
“农场主假说”则有一层令人不安的恐怖色彩:一个农场里有一群火鸡,农场主每天中午十一点来给它们喂食。火鸡中的一名科学家观察这个现象,一直观察了近一年都没有例外,于是它也发现了自己宇宙中的伟大定律:“每天上午十一点,就有食物降临。”它在感恩节早晨向火鸡们公布了这个定律,但这天上午十一点食物没有降临,农场主进来把它们都捉去杀了。
在这个例子中,问题是,火鸡愚蠢吗?
观点2就是“没有免费的午餐”。这是在“数学现实”中成立的,在“数学现实”中,一切可能性都存在,感恩节那天,火鸡有可能被杀,也有可能被农场主的孩子当成宠物,也有可能农场主决定把一部分鸡再养一年然后杀掉。鸡无论做出怎样的猜想都可能落空。可以证明,无论我们学习到了什么东西,或者掌握到了什么规律,我们总是可以(在数学上)构造一个反例(比如,让太阳从西边升起,让黄金变成泥土),与我们的判断不一致。这不管对于机器,而是对于人,都是一样的。也就是在“一般“的意义上,或者数学的意义上,没有哪个生物,或者哪个算法,在预测能力上比瞎猜更好。
而看似矛盾的观点1,却在物理现实中得以成立。可以说,物理定律是一部分不能用数学证明的真理。我们相信这些定律,一是因为我们尚且没有发现违背的情况,二是某种直觉告诉我们它很可能是对的。为什么我们能总结出这些定律,这是一个让人困惑的问题,因为看起来人并不是先天就能总结出各种定律。但是可以确定的是,我们本身就是定律约束下进化的产物,虽然对物理定律的理解不是我们的本能,但是很多“准定律”已然成为我们的本能,它们塑造了我们本能的思考问题的方式,对对称性的理解,等等等等。
现实中的情况介于观点1和观点2之间。很多东西既不是完全没有规律,也不是一种物理定律,但是对我们的进化和存活意义重大(也就是上面说的“准定律”),它们是一种非常强的“先验分布”,或者说,是我们的常识,而且我们通常情况下意识不到这种常识。
既然不是物理定律,那么按照观点2,我们就能够找到一些反例。这些反例对我们来说是某种“错误”,这种错误正是非常非常强的证据,它揭示了一些我们的本能。
而认知神经科学就可以通过一些实验揭示出这些错误。下面给出一些例子:
一个例子是下面的人脸:
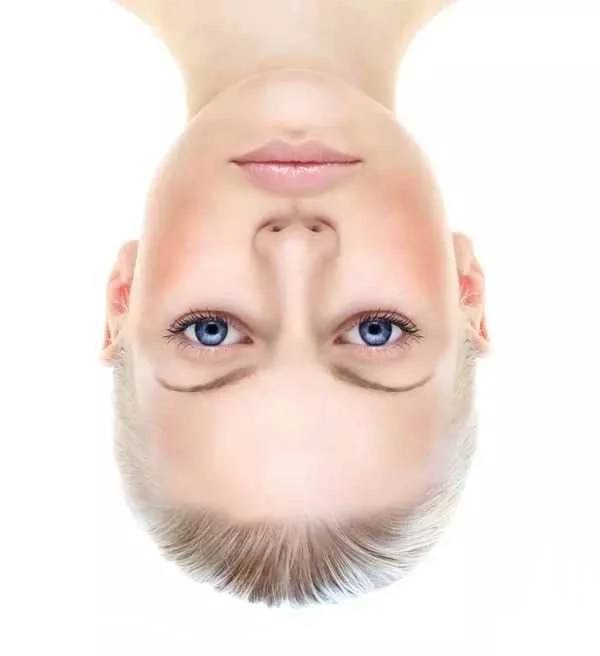
这个人是什么样的表情?倒过来再看看?
这个例子说明了人对倒过来的人脸的表情的识别能力很差。长期的进化过程中,我们对正着的人脸造成了“过拟合”,“正着”的信息变得不是很重要。上面的图出现错觉的原因是,虽然人脸是倒着的,我们却用“正着”的思路观察图片中眼睛,而眼睛的线条走向给了我们表情信息:
(甚至一些简单的线条,都会让我们觉得是人脸,并且得出它的表情。其中眼睛和嘴的线条在我们表情识别中起了重要作用)

这启示我们,人类识别脸,其实就是通过几个关键的结构(眼睛,眉毛,嘴,鼻子)完成的。当今很多算法都模仿这一点,标注出人脸的关键结构,成功率很高。
另外人对脸的形状过拟合,也让我们看二次元中动画人物的脸时觉得很正常,实际上这和真实的脸差异很大,但是我们大脑不这么认为,因为这种识别机制已经成为了我们的本能。
第二个例子是这个错觉图:

很难想象,A和B的颜色居然是一样的。

造成这个错觉的原因是,对了对应自然界中阴影对颜色识别的副作用,我们大脑擅自“减去”了阴影对颜色的影响。在进化中,我们正如火鸡一样,觉得“每天上午十一点,就有食物降临”;同样的,我们觉得“把阴影对颜色的干扰消除掉,就能识别得更好”,这成为了我们的“准定律”。然而,上面的错觉图中,要求我们比较A和B的颜色,就好似感恩节对火鸡一样,我们大脑仍然不听话地擅自改变颜色,导致我们在这个极其特殊的问题上判断失误。只不过这个失误不导致什么后果罢了,当然如果外星人打算利用这个失误作为我们的弱点来对付我们,那就是另外一种剧情。
下面这个图片是更加极端的情况。中间的条带其实没有渐变。
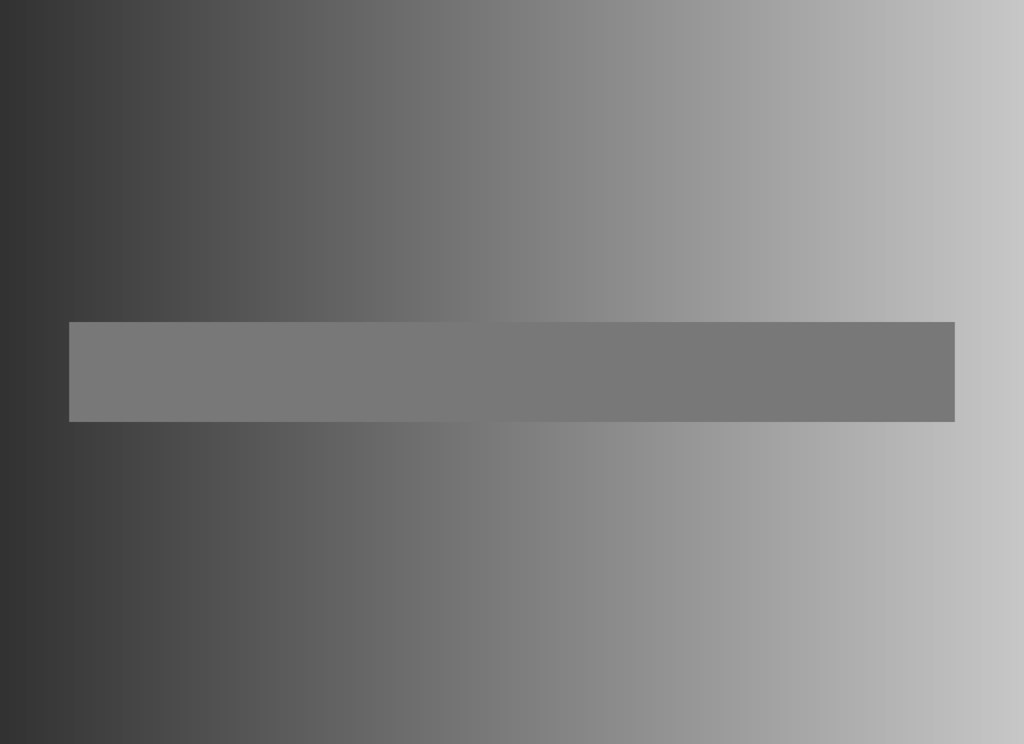
第三个错觉是关于线条的:
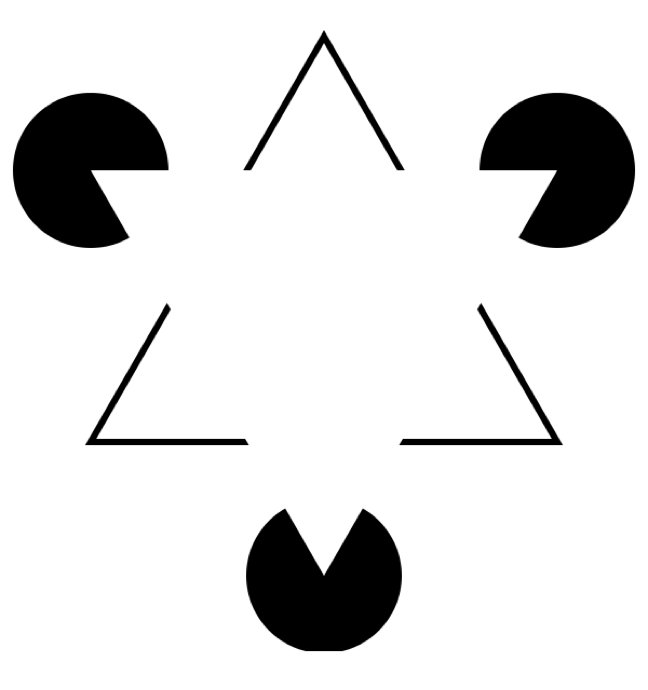
人类会不由自主的觉得中间似乎有个白色三角形,因为我们大脑“骗”我们,让我们觉得似乎有一些“看不见的边”。
把效果变得更夸张一点:

按照一定距离观察这幅图,会让我们觉得产生了“缠绕”或者“扭曲”。实际上这些就是一个个同心圆。产生错觉的原因是,大脑给我们“脑补”了很多倾斜边(这些方块是倾斜的,并且采用了不同的颜色加强边的效果),这些边的形状不同于它们的排列方向,因此会觉得“缠绕”。如果我们到了这样的图案居多的世界中,我们的现在视觉系统将难以正常工作。
我们生活中的绝大多数物体,都有着明确的边界。这不是一个物理定律,但是就其普遍性而言,足够成为一个“准定律”。以至于人和动物的大脑视觉皮层拥有专门识别边的结构:
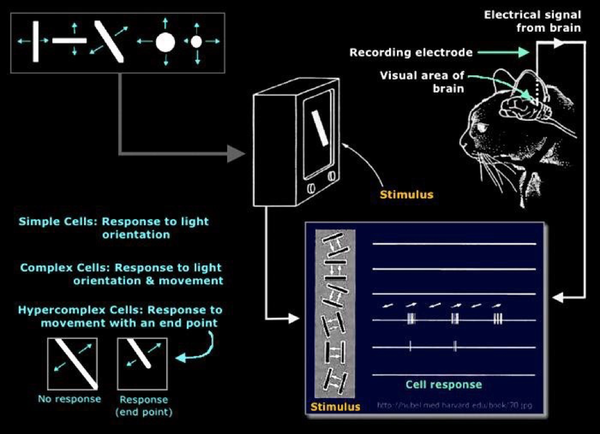
CNN 被认为在生物学上收到支持的原因之一,在于能够通过学习自动得到边缘等特征的filter(非常像所谓的 Gabor filter):

CNN成功之处在于能够非常成功的抽取到图像的特征。这在 Neural Style 项目的风格迁移(原图+风格->带风格的原图)中表现得非常好:

人类的这些错觉同时也暗示了人类和算法模型一样受“没有免费午餐定理”的限制,人的认知并没有特别异于算法的地方,或许是可以被算法复现的。
说 Hinton 是一个认知神经科学家并没有问题。Hinton做过不少认知实验,也在认知科学领域发过不少论文。
Hinton自己也承认,CNN做的非常好。但是当Hinton做了一系列认知神经科学的试验后,HInton 觉得有些动摇,直至他现在反对CNN。
第一个实验称为四面体谜题(tetrahedron puzzle),也是 Hinton 认为最有说服力的实验。
如图,有两个全等的简单积木,要求你把它们拼成一个正四面体(不要看答案,先自己试试)。

这理应是个非常非常简单的问题,对于类似的问题,人们平均能在5秒内解决。但是Hinton 惊讶的发现,对于这个问题人们平均解决的时间超乎意料的长,往往要几十秒甚至几分钟。

(视频中Hinton亲自演示这个实验的样子很有趣)
Hinton 此处狂黑MIT,说MIT教授解决这个问题的分钟数和和他们在MIT工作的年数基本一致,甚至有一个MIT教授看来半天写了一个证明了说这是不可能的(然后底下MIT的学生听了非常高兴,他们很喜欢黑自己的教授)。
但是两类人解决得非常快,一类是本来就对四面体的构型非常了解的;另外就是不认真对待随便瞎试的(毕竟就几种可能情况,枚举起来很快)。但是如果希望通过观察,通过视觉直觉解决问题会非常困难。
这意味着我们出现了错觉,而且是一种视觉错觉。
Hinton 通过人们尝试的过程发现,错觉是由于人们不自觉地会根据物体形状建立一种“坐标框架”(coordinate frame)
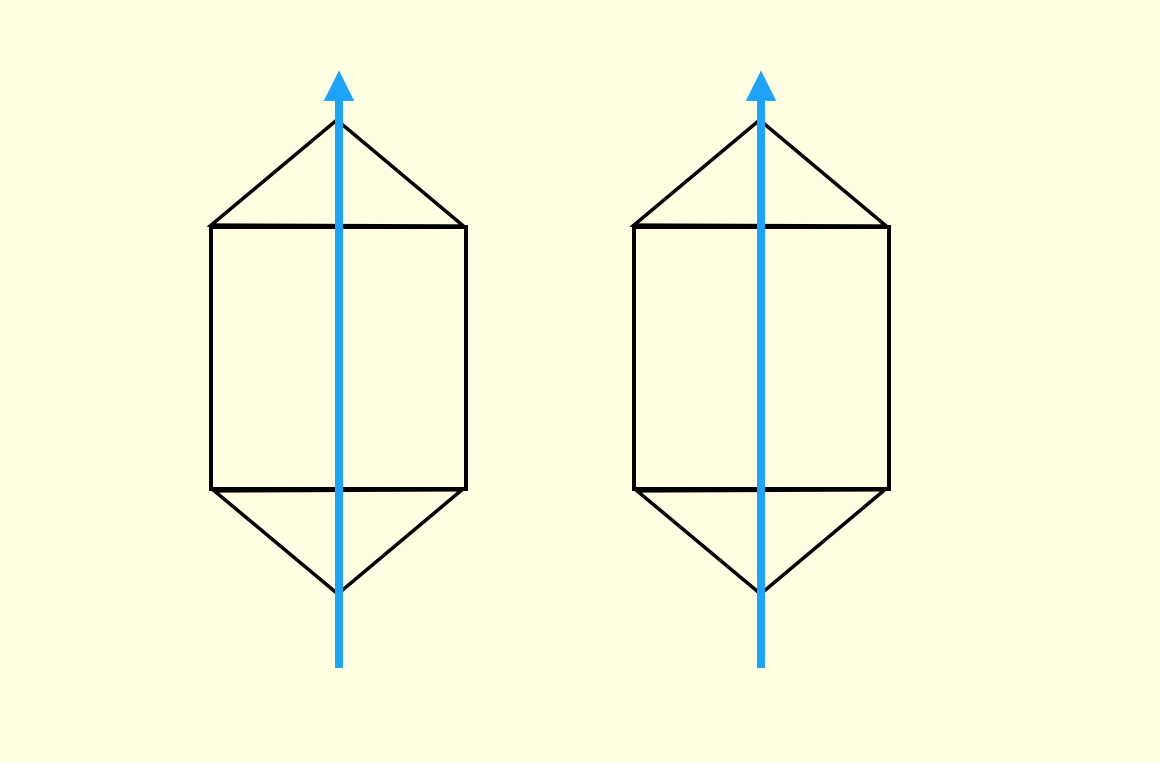
人们会不自主地给两个全等的几何体使用相同的坐标框架。这个坐标框架会造成误导,导致人们总是先尝试一些错误的解。
如果给两个几何体不同的坐标框架
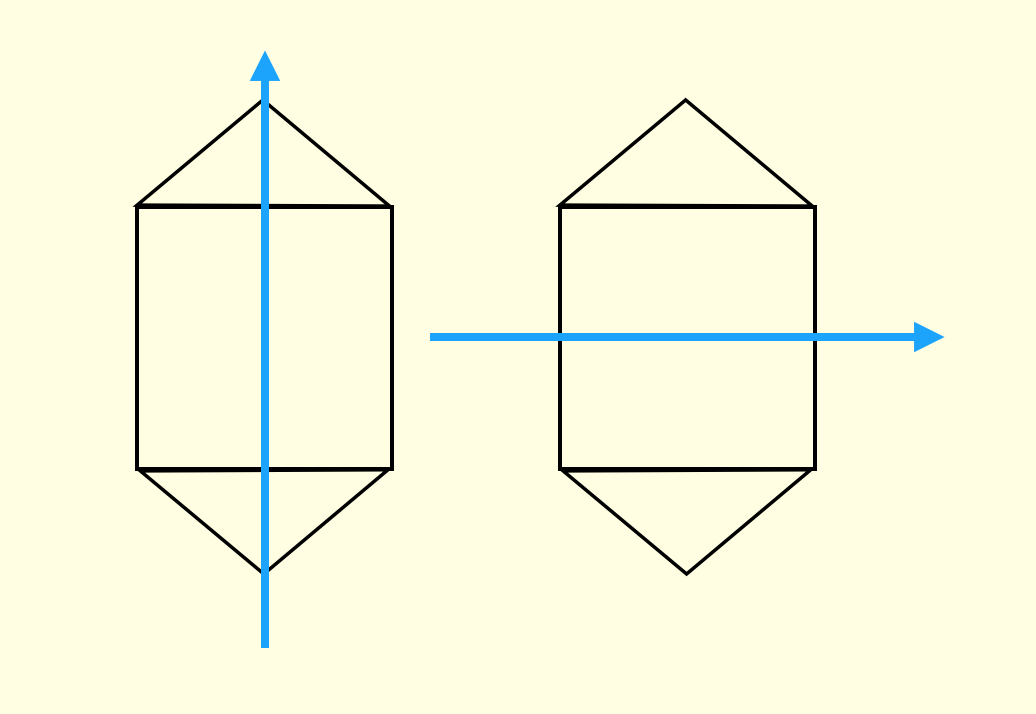
几乎就立即可以得到解
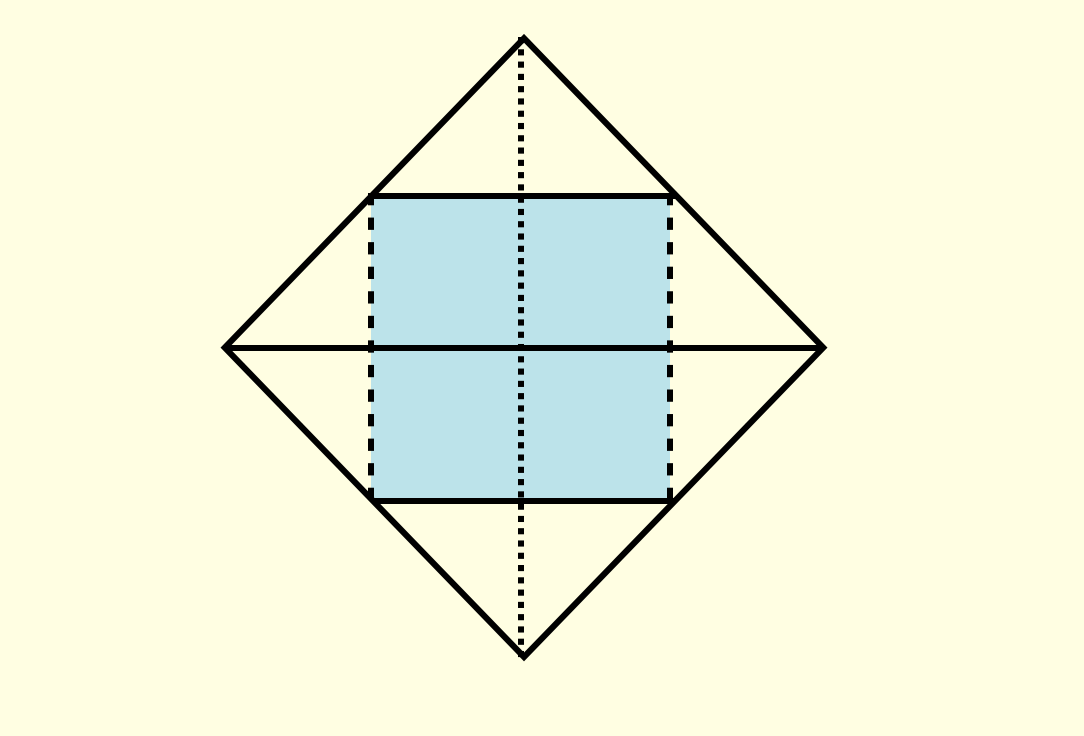
第二个实验关于手相性(handedness),手相性不一致的结构不能通过平面旋转重合。这个做有机化学的同学应该最熟了(各种手性碳),比如被手向性控制的恐惧(来报一下岩沙海葵毒素的IUPAC命名?):

最简单的手相性就是分清左右,这个到现在很多人都会搞混。判断手相性对人来说是很困难的。Hinton 给的例子是“意识旋转”(mental rotation),这个问题是判断某两个图形的手相性是否一致:
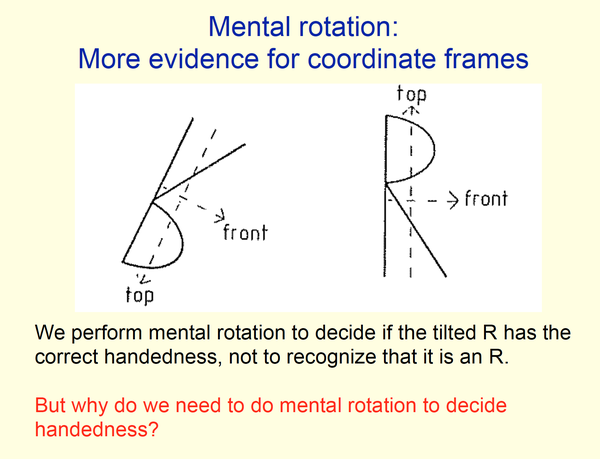
我们无法直接回答,而是要在意识中“旋转”某个R,才能判断手相性是否一致。并且角度差的越大,人判断时间就越长。
而“意识旋转”同样突出了“坐标框架”的存在,我们难以判断手相性,是因为它们有不一致的坐标框架,我们需要通过旋转把坐标框架变得一致,才能从直觉上知道它们是否一致。
第三个实验是关于地图的。我们需要让一个对地理不是特别精通,但是有基础知识的人,回答一个简单的问题:
下面的图案是什么洲?
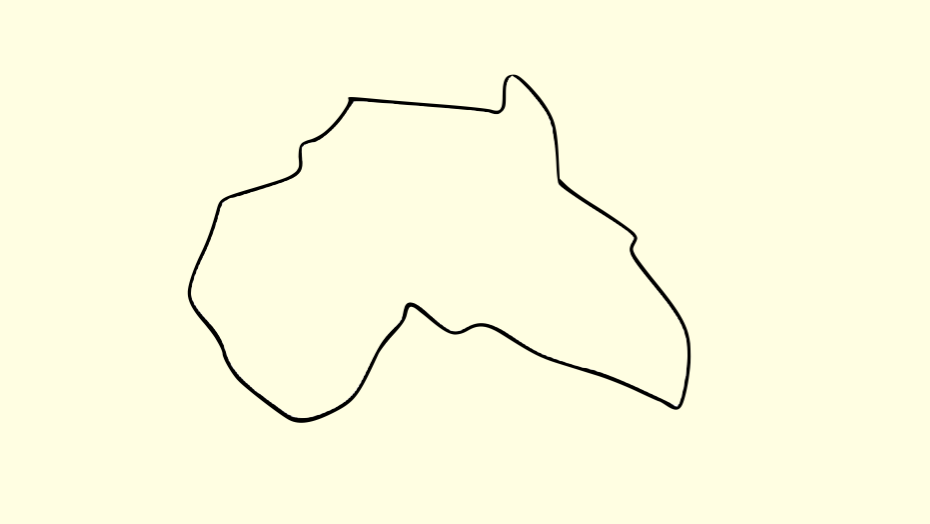
相当多的人(特别是凭直觉直接答的)回答,像澳洲。
这是因为对于不规则图案,我们想当然地建立了这样的坐标框架:
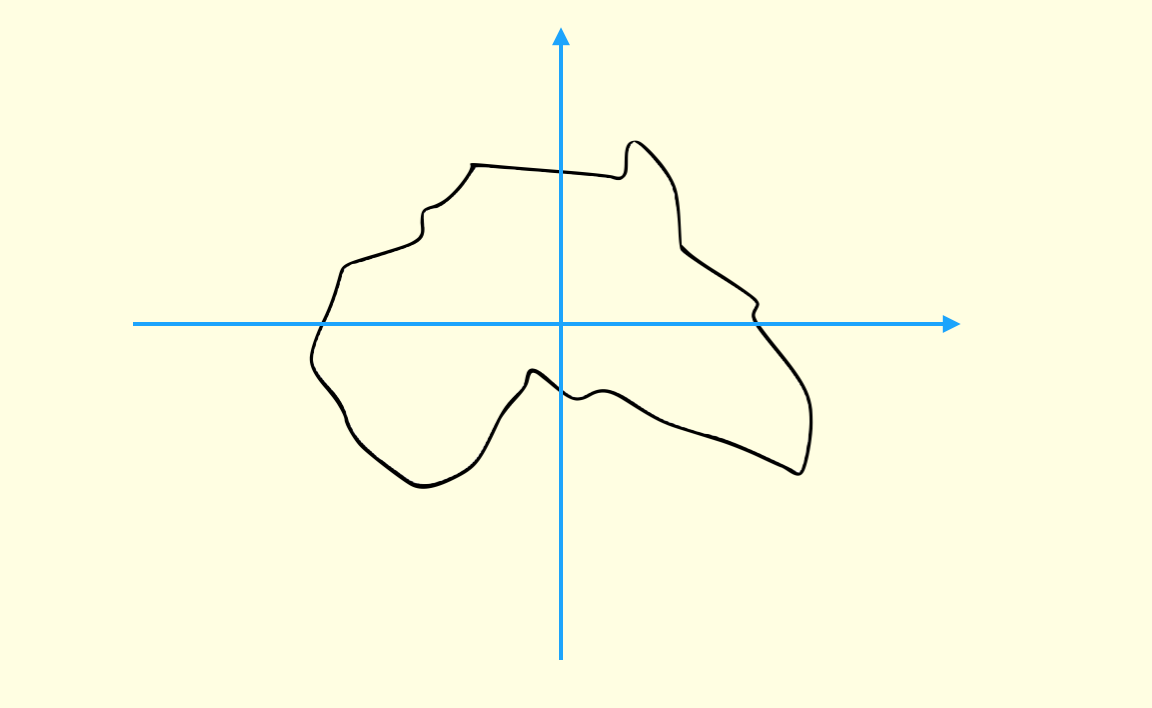
但是如果你这样建立:
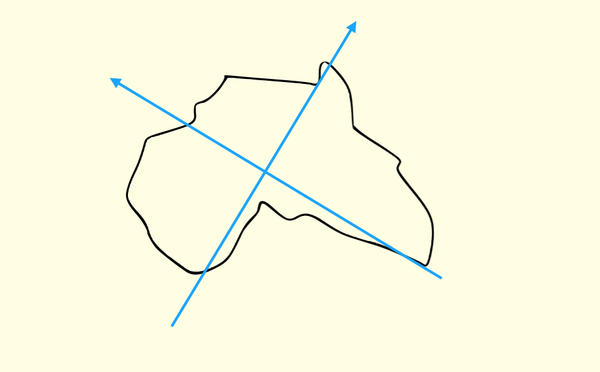
就会立即发现这是非洲,而且和澳洲相差的挺大。
通过这几个实验,Hinton得出了这样的结论:
人的视觉系统会建立“坐标框架”,并且坐标框架的不同会极大地改变人的认知。
但是在CNN上却很难看到类似“坐标框架”的东西。
Hinton 提出了一个猜想:
物体和观察者之间的关系(比如物体的姿态),应该由一整套激活的神经元表示,而不是由单个神经元,或者一组粗编码(coarse-coded,这里意思是指类似一层中,并没有经过精细组织)的神经元表示。
而这一整套神经元,Hinton认为就是Capsule。
Hinton 反对 CNN的另外一个理由是,CNN的目标不正确。问题主要集中在 Pooling 方面(我认为可以推广到下采样,因为现在很多CNN用卷积下采样代替Pooling层)。Hinton认为,过去人们对Pooling的看法是能够带来 invariance 的效果,也就是当内容发生很小的变化的时候(以及一些平移旋转),CNN 仍然能够稳定识别对应内容。
但是这个目标并不正确,因为最终我们理想的目标不是为了“识别率”,而是为了得到对内容的良好的表示(representation)。如果我们找到了对内容的良好表示,那么就等于我们“理解”了内容,因为这些内容可以被用来识别,用来进行语义分析,用来构建抽象逻辑,等等等等。而现在的 CNN 却一味地追求识别率,这不是Hinton想要的东西,Hinton想要 “something big”。
Hinton的看法是,我们需要 Equivariance 而不是 Invariance。
所谓 Invariance,是指表示不随变换变化,比如分类结果等等。
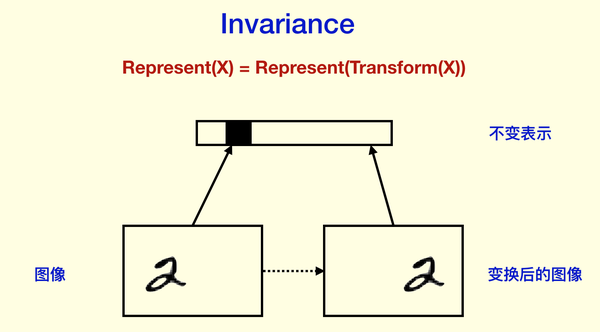
Invariance 主要是通过 Pooling 等下采样过程得到的。如果你对训练神经网络有经验,你可能会想到我们在做图像预处理和数据拓增的时候,会把某些图片旋转一些角度,作为新的样本,给神经网络识别。这样CNN能够做到对旋转的 invariance,并且是“直觉上”的invariance,根本不需要像人那样去旋转图片,它直接就“忽视”了旋转,因为我们希望它对旋转invariance。
CNN同样强调对空间的 invariance,也就是对物体的平移之类的不敏感(物体不同的位置不影响它的识别)。这当然极大地提高了识别正确率,但是对于移动的数据(比如视频),或者我们需要检测物体具体的位置的时候,CNN本身很难做,需要一些滑动窗口,或者R-CNN之类的方法,这些方法很反常(几乎肯定在生物学中不存在对应结构),而且极难解释为什么大脑在识别静态图像和观察运动场景等差异很大的视觉功能时,几乎使用同一套视觉系统。
对平移和旋转的 invariance,其实是丢弃了“坐标框架”,Hinton认为这是CNN不能反映“坐标框架”的重要原因。
而 equivariance 不会丢失这些信息,它只是对内容的一种变换:

Hinton 认为 CNN 前面非 Pooling 的部分做的很好,因为它们是 equivariance 的。
那么在 Capsule 的框架下,又应该如何体现 equivariance 呢?
Hinton 认为存在两种 equivariance:
并且,两者的联系是,高层的 capsule 有更广的域 (domain),所以低层的 place-coded 信息到高层会变成 rate-coded。
这里Hinton虽然没有指明,但是我感觉到 Hinton 是希望能够统一静态视觉和动态视觉的(通过两种编码方式,同时感知运动和内容)。人脑中对于静态和动态内容的处理通路并没有特别大的变化,但是现在做视频理解的框架和做图片理解的差异还是不小的。
但是,毕竟 invariance 是存在的,比如我们对物体的识别确实不和物体的位置有关。这里Hinton解释了一下:
knowledge,but not activities have to be invariant of viewpoint
也就是Hinton谈论的问题是关于 activation 的,之前人们所说的CNN的 invariance 是关于神经元 activation 的。Hinton 希望 invariance 仅仅是对于 knowledge 的(对于Capsule而言,是其输出的概率部分)。通过这可以看到Hinton使用Capsule的一个原因是觉得Capsule相比单个神经元更适合用来做表示。
那么高层的 Capsule 怎么从底层的 Capsule 获取信息呢?
首先 Capsule 的输出是什么?
Hinton 假设 Capsule 输出的是 instantiation parameters (实例参数) ,这是一个高维向量:
Capsule 的核心观念是,用一组神经元而不是一个来代表一个实体,且仅代表一个实体。
然后通过对底层的 Capsule 做 coincidence filtering (巧合筛分)决定激活哪些高层的Capsule 。coincidence filtering是一种通过对高维度向量进行聚类来判断置信的方式,Hinton举了一个例子:
比如你在街上听到有人谈论11号的纽约时报,你一开始可能并不在意;但是如果你沿路听到4个或者5个不同的人在谈论11号的纽约时报,你可能就立即意识到一定有什么不平常的事情发生了
我们的(非日常)语句就像高维空间中向量,一组相近语句的出现,自然条件下概率很小,我们会很本能地筛分出这种巧合。
coincidence filtering 能够规避一些噪声,使得结果比较 robust。
这让我想起了现在CNN容易被对抗样本欺骗的问题。虽然几乎所有的机器学习模型都存在对抗样本的问题,但是CNN可以被一些对人而言没有区别的对抗样本欺骗,这是严峻的问题(这也是CNN易于我们视觉系统的一点)。一部分原因在于NN的线性结构,其对噪声的耐受不是很好。不知道 coincidence filtering 能否缓解这个问题。
用图来表示(知乎怎么传高清图啊)就像这样:
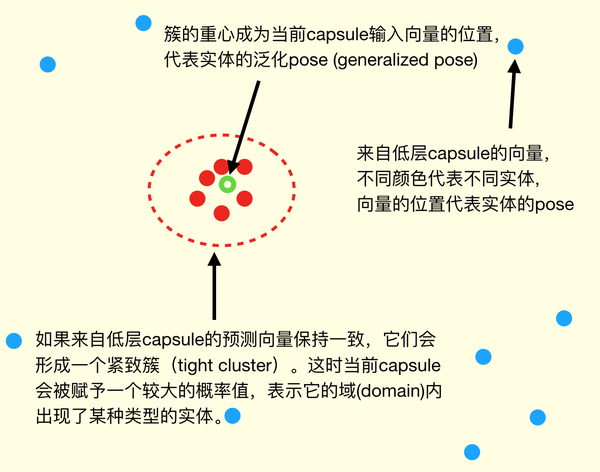
Hinton采用的聚类(他称为Agree)方式是使用以下评估:
其中 mixture 是gaussian mixture,可以通过EM算法得到。也就是,如果簇的形状越接近高斯分布(也就是越集中),得分越高;反之越分散越接近均匀分布,得分越低:
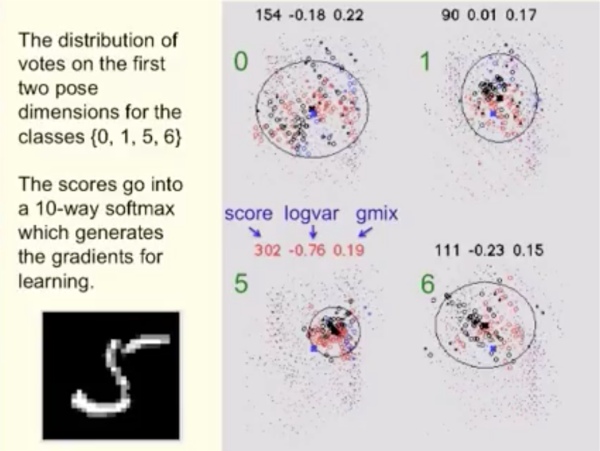
得到高分的簇的分类会对应的上层capsule会接受下层capsule提供的generalized pose,相当于做了routing。这是因为下层的这些输出,“选择”了上层的capsule,“找到最好的(处理)路径等价于(正确)处理了图像”,Hinton 这样解释。Hinton 称这种机制为 “routing by agreement”。
这种 routing 不是静态的,而是动态的(随输入决定的),这是 Pooling 等方式不具备的:
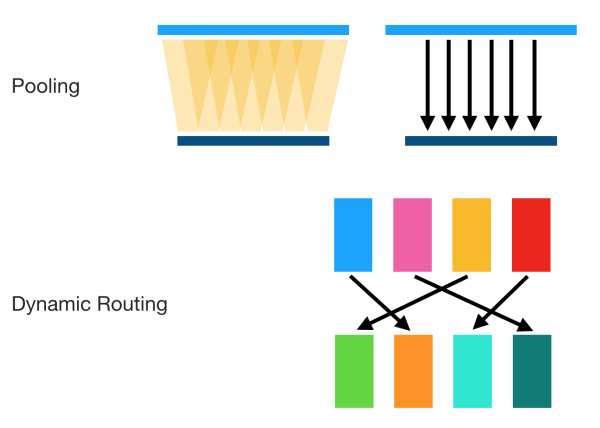
由于使用这种类似聚类的方式,其有潜在的 unsupervised learning 的能力,不过Hinton还没有透露具体的算法。
Hinton 这次明显受到了计算机图形学的启发。他在报告[2]中说 literally,literally, reverse of graphics. (我非常非常认真地想要“逆向”图形学)。
计算机图形学中有个非常重要的性质,就是其使用了 linear manifold,有良好的视角不变性。
说明白一点,也就是用视角变换矩阵作用到场景中,不改变场景中物体的相对关系。
于是Hinton决定用矩阵处理两个物体间的关联。
按照上面的 routing by agreement 的算法,如果我们希望从 mouth 和 nose 得到 face,我们需要让mouth的向量 和 nose 的向量
基本一致。
它们本身肯定不会一致的,因为 mouth 和 nose 不是一样的东西;要让它们一致我们就需要找一类函数,使得 。
但是选择哪类函数呢?Hinton的答案是多重线性函数(矩阵),因为这能够使得它们的关系不受视角变换(设视角变换为矩阵W)影响,这是因为
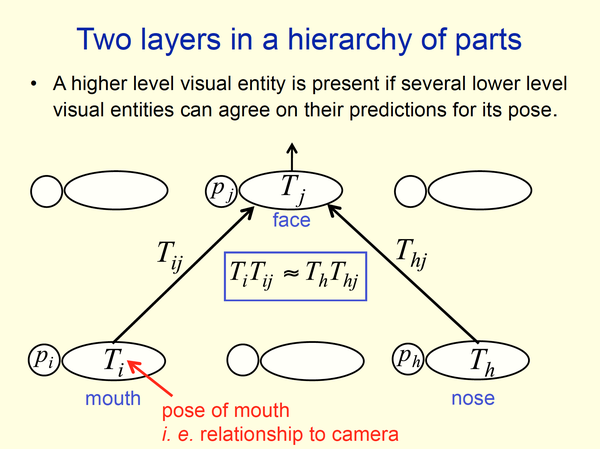
而且这对三维也是有效的,这里看到了 Hinton 冲击三维视觉的野心。
Hinton 是个很“固执”的人,在 Andrew Ng 对他的采访中,他说出了自己的想法:
If your intuitions are good, you should follow them and you will eventually be successful; if your intuitions are not good, it doesn‘t matter what you do. You might as well trust your intuitions there‘s no point not trusting them.
(意思是如果直觉一直很好,那么当然应该坚持;如果直觉很差,那么怎么做也没有关系了(反正你也搞不出什么,即使你换个想法大抵也不会成功))。当然后半句可能是 Hinton 的高级黑。
但是 Hinton 确乎坚信自己的直觉,从反向传播提出,到深度学习的火爆,Hinton已经坚守了30年了,并没有任何放弃的意思。
现在 Capsule 给了 Hinton 很多直觉,Hinton 估计也是会一条路走到黑。
如果Hinton会失败,大抵是两种情况,
第一种是因为现在反向传播的各种优点,上面已经总结过了。
第二种是因为即使一个直觉特别好的人,也有可能有直觉特别不好的一天,尤其是晚年。这点非常著名的例子是爱因斯坦。爱因斯坦性格和 Hinton 很像,有非常敏锐的直觉,并且对自己的直觉的值守到了近乎固执的程度。爱因斯坦晚年的时候,想要搞统一场论,这是一个很大的目标,就好像现在Hinton希望能够创造颠覆BP机制的目标一样;爱因斯坦也获得了很多直觉,比如他觉得电磁场和引力是非常相似的,都和相对论紧密关联,都是平方反比,都是一种传递力的波色子,并且玻色子静质量都是0,力的范围都是无穷远,等等等等,就好像现在Hinton找到的各种各样很有说服力的论据一样;于是爱因斯坦决定首先统一电磁力和引力,结果是失败的。反而是两种看上去很不搭的力——弱相互作用力(3种玻色子,范围在原子核大小内)和电磁力首先被统一了(电弱统一理论)。而引力恰恰是目前最难统一的,也就是爱因斯坦的直觉走反了。我很担心 Hinton 也会如此。
不过即使爱因斯坦没有成功,后人也为其所激励,继续扛起GUT的大旗推动物理前沿;对于Hinton 我想也是一样。
Hinton 曾经在1987年左右发明了 recirculation 算法代替BP来训练神经网络,虽然不算特别成功,但是却预言了后来神经科学才发现的spike timing-independent plasticity。
Hinton 最初提出 capsule 的时候(5年前),几乎“逢投必拒”,没有人相信,但是 Hinton 自己一致坚信这一点,并且一直坚持到现在。
在 Andrew Ng对其采访中,Hinton 对未来的趋势(对CS从业者)的一句很有意思的描述:showing computers is going to be as important as programming computers.
[1] 2017年8月17日,于加拿大多伦多大学 Fields Institute,Hinton 的报告 https://www.youtube.com/watch?v=Mqt8fs6ZbHk
[2] 2017年4月3日发布 Brain & Cognitive Sciences 于 MIT,Hinton 的报告 https://www.youtube.com/watch?v=rTawFwUvnLE
[3] 媒体报道 Hinton 要将当前的深度学习核心算法推倒重来 Artificial intelligence pioneer says we need to start over
[4] Fei-Fei Li 在 Twitter 上的评论:Echo Geoff‘s sentiment no tool is eternal, even backprop or deeplearning. V. important to continue basic research.
[5] Le, Q. V. (2013, May). Building high-level features using large scale unsupervised learning. In Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on (pp. 8595-8598). IEEE.
[6] Bény, C. (2013). Deep learning and the renormalization group. arXiv preprint arXiv:1301.3124.
[7] Hinton, G. (2010). A practical guide to training restricted Boltzmann machines. Momentum, 9(1), 926.
[8] Rina Decher (1986). Learning while searching in constraint-satisfaction problems. University of California, Computer Science Department, Cognitive Systems Laboratory.
[9] Hinton, G. E., Krizhevsky, A., & Wang, S. D. (2011, June). Transforming auto-encoders. In International Conference on Artificial Neural Networks (pp. 44-51). Springer Berlin Heidelberg.
[10] Wolpert, D. H. (1996). The lack of a priori distinctions between learning algorithms. Neural computation, 8(7), 1341-1390.
[11] Hinton, G. E., & McClelland, J. L. (1988). Learning representations by recirculation. In Neural information processing systems (pp. 358-366).
原文地址: https://zhuanlan.zhihu.com/p/29435406
标签:batch 时报 枚举 输出 激活 pac status 物理学 构造
原文地址:http://www.cnblogs.com/DjangoBlog/p/7922359.html