【机器学习笔记】自组织映射网络（SOM）

什么是自组织映射？

一个特别有趣的无监督系统是基于竞争性学习，其中输出神经元之间竞争激活，结果是在任意时间只有一个神经元被激活。这个激活的神经元被称为胜者神经元（winner-takes-all neuron）。这种竞争可以通过在神经元之间具有横向抑制连接（负反馈路径）来实现。其结果是神经元被迫对自身进行重新组合，这样的网络我们称之为自组织映射（Self Organizing Map，SOM）。

拓扑映射

神经生物学研究表明，不同的感觉输入（运动，视觉，听觉等）以有序的方式映射到大脑皮层的相应区域。

这种映射我们称之为拓扑映射，它具有两个重要特性：

• 在表示或处理的每个阶段，每一条传入的信息都保存在适当的上下文（相邻节点）中
• 处理密切相关的信息的神经元之间保持密切，以便它们可以通过短突触连接进行交互

我们的兴趣是建立人工的拓扑映射，以神经生物学激励的方式通过自组织进行学习。

我们将遵循拓扑映射形成的原则：“拓扑映射中输出层神经元的空间位置对应于输入空间的特定域或特征”。

建立自组织映射

SOM的主要目标是将任意维度的输入信号模式转换为一维或二维离散映射，并以拓扑有序的方式自适应地执行这种变换。

因此，我们通过将神经元放置在一维或二维的网格节点上来建立我们的SOM。更高的尺寸图也是可能的，但不是那么常见。

在竞争性学习过程中，神经元有选择性地微调来适应各种输入模式（刺激）或输入模式类别。如此调整的神经元（即获胜的神经元）的位置变得有序，并且在该网格上创建对于输入特征有意义的坐标系。因此，SOM形成输入模式所需的拓扑映射。我们可以将其视为主成分分析（PCA）的非线性推广。

映射的组织结构

输入空间中的点\(\mathbf x\)映射到输出空间中的点\(I(\mathbf x)\)，如图所示

其中。每一个输出空间中的点\(I\)将会映射到对应输入空间中的点\(\mathbf w(I)\)

Kohonen网络

我们将专注于被称为Kohonen网络的特定类型的SOM。 这个SOM（以二维映射为例）有一个前馈结构，以行列方阵构成的单一计算层。每个神经元完全连接到输入层中的所有源节点：

显然，如果是一维的映射，那么在计算层中只有一行（或一列）。

自组织的过程

自组织的过程包括以下四个主要方面：

• 初始化：所有连接权重都用小的随机值进行初始化。
• 竞争：对于每种输入模式，神经元计算它们各自的判别函数值，为竞争提供基础。具有最小判别函数值的特定神经元被宣布为胜利者。
• 合作：获胜的神经元决定了兴奋神经元拓扑邻域的空间位置，从而为相邻神经元之间的合作提供了基础。
• 适应：受激神经元通过适当调整相关的连接权重，减少与输入模式相关的判别函数值，使得获胜的神经元对相似输入模式的后续应用的响应增强。

竞争过程

如果输入空间是\(D\)维（即有\(D\)个输入单元），我们可以把输入模式写成\(\mathbf{x} = \{x_i:i=1,...,D\}\)，输入单元\(i\)和神经元\(j\)之间在计算层的连接权重可以写成\(\mathbf{w}_j=\{w_{ji}:j=1,...,N;i=1,...,D\}\)，其中\(N\)是神经元的总数。

然后，我们可以将我们的判别函数定义为输入向量\(\mathbf x\)和每个神经元\(j\)的权向量\(\mathbf{w}_j\)之间的平方欧几里德距离
\[d_j(\mathbf{x})=\sum_{i=1}^{D}(x_i-w_{ji})^2\]
换句话说，权重向量最接近输入向量（即与其最相似）的神经元被宣告为胜利者。这样，连续的输入空间可以通过神经元之间的一个简单的竞争过程被映射到神经元的离散输出空间。

合作过程

在神经生物学研究中，我们发现在一组兴奋神经元内存在横向的相互作用。当一个神经元被激活时，最近的邻居节点往往比那些远离的邻居节点更兴奋。并且存在一个随距离衰减的拓扑邻域。

我们想为我们的SOM中的神经元定义一个类似的拓扑邻域。 如果\(S_{ij}\)是神经元网格上神经元\(i\)和\(j\)之间的横向距离，我们取
\[T_{j,I(x)}=\exp(-\frac{S^2_{j,I(x)}}{2\sigma^2})\]
作为我们的拓扑邻域，其中\(I(\mathbf{x})\)是获胜神经元的索引。该函数有几个重要的特性：它在获胜的神经元中是最大的，且关于该神经元对称，当距离达到无穷大时，它单调地衰减到零，它是平移不变的（即不依赖于获胜的神经元的位置）。

SOM的一个特点是\(\sigma\)需要随着时间的推移而减少。常见的时间依赖性关系是指数型衰减：\(\sigma(t)=\sigma_0\exp(-t/\tau_\sigma)\)

适应过程

显然，我们的SOM必须涉及某种自适应或学习过程，通过这个过程，输出节点自组织，形成输入和输出之间的特征映射。

地形邻域的一点是，不仅获胜的神经元能够得到权重更新，它的邻居也将更新它们的权重，尽管不如获胜神经元更新的幅度大。在实践中，适当的权重更新方式是
\[\Delta w_{ji}=\eta(t) \cdot T_{j,I(x)}(t) \cdot (x_i-w_{ji})\]
其中我们有一个依赖于时间的学习率\(\eta(t)=\eta_0\exp(-t/\tau_\eta)\)，该更新适用于在多轮迭代中的所有训练模式\(\mathbf x\)。

每个学习权重更新的效果是将获胜的神经元及其邻居的权向量\(w_i\)向输入向量\(\mathbf x\)移动。对该过程的迭代进行会使得网络的拓扑有序。

排序和收敛

如果正确选择参数（\(\sigma_0,\tau_\sigma,\eta_0,\tau_\eta\)），我们可以从完全无序的初始状态开始，并且SOM算法将逐步使得从输入空间得到的激活模式表示有序化。（但是，可能最终处于特征映射具有拓扑缺陷的亚稳态。）

这个自适应过程有两个显著的阶段：

• 排序或自组织阶段：在这期间，权重向量进行拓扑排序。通常这将需要多达1000次的SOM算法迭代，并且需要仔细考虑邻域和学习速率参数的选择。

• 收敛阶段：在此期间特征映射被微调（fine tune），并提供输入空间的精确统计量化。通常这个阶段的迭代次数至少是网络中神经元数量的500倍，而且参数必须仔细选择。

可视化自组织过程

• 假设我们在连续的二维输入空间中有四个数据点（\(\times\)），并且希望将其映射到离散一维输出空间中的四个点上。输出节点映射到输入空间中的点（\(\circ\)）。随机初始化权重使得\(\circ\)的起始位置落在随机落在输入空间的中心。
  
• 我们随机选择一个数据点（\(\otimes\)）进行训练。最接近的输出点表示获胜的神经元（\(\blacklozenge\)）。获胜的神经元向数据点移动一定量，并且两个相邻的神经元以较小的量移动（箭头指示方向）。
  
• 接下来，我们随机选择另一个数据点进行训练（\(\otimes\)）。最接近的输出点给出新的获胜神经元（\(\blacklozenge\)）。获胜的神经元向数据点移动一定量，并且一个相邻的神经元也朝该数据点移动较小的量（箭头指示方向）。
  
• 我们随机挑选数据点进行训练（\(\otimes\)）。每个获胜的神经元向数据点移动一定的量，其相邻的神经元以较小的量向数据点移动（箭头指示方向）。最终整个输出网格将自身重新组织以表征输入空间。
  

SOM算法总结

我们有一个空间连续的输入空间，其中包含我们的输入向量。我们的目的是将其映射到低维的离散输出空间，其拓扑结构是通过在网格中布置一系列神经元形成的。我们的SOM算法提供了称为特征映射的非线性变换。

SOM算法过程总结如下：

1. 初始化 - 为初始权向量\(\mathbf w_j\)选择随机值。
2. 采样 - 从输入空间中抽取一个训练输入向量样本\(\mathbf x\)。
3. 匹配 - 找到权重向量最接近输入向量的获胜神经元\(I(\mathbf x)\)。
4. 更新 - 更新权重向量 \(\Delta w_{ji}=\eta(t) \cdot T_{j,I(x)}(t) \cdot (x_i-w_{ji})\)
5. 继续 - 继续回到步骤2，直到特征映射趋于稳定。

形象化理解

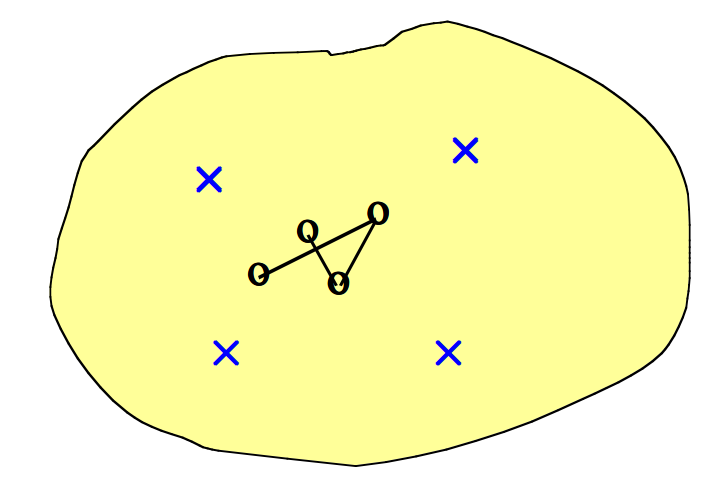
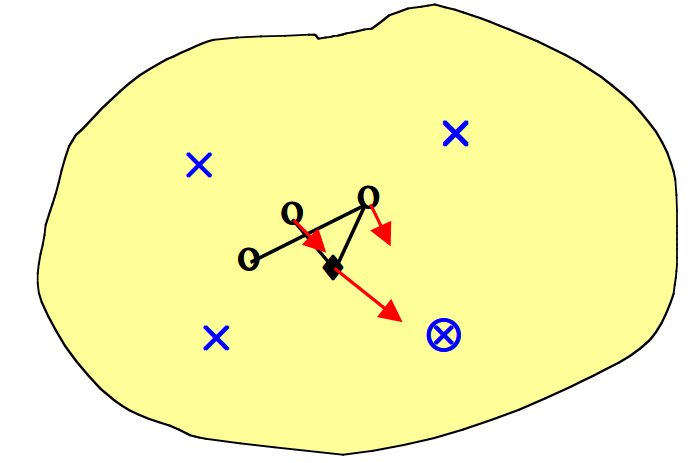
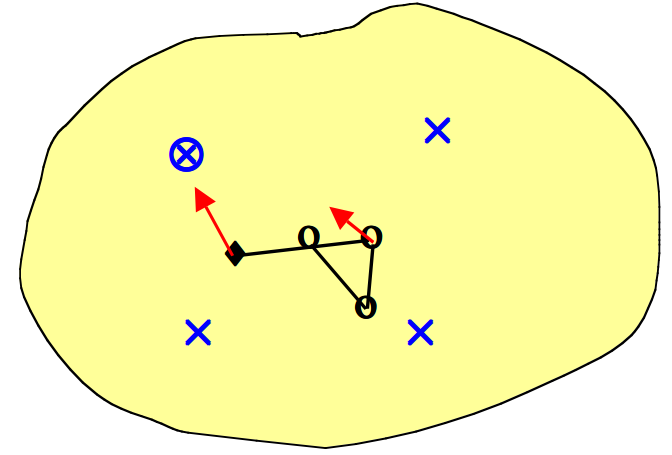
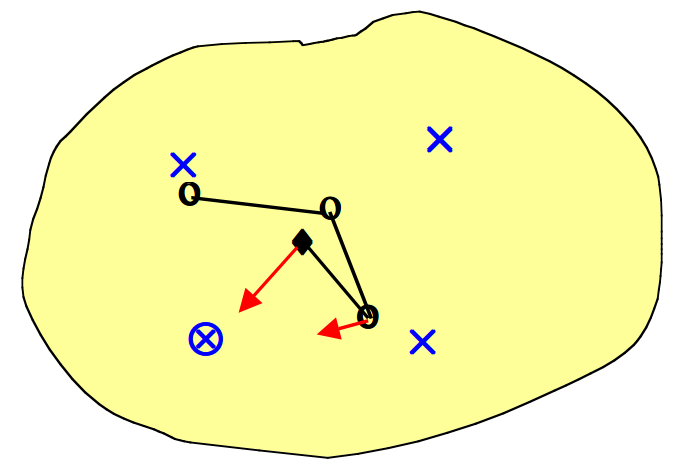
我们来看维基百科上给出的一个SOM学习过程示意图，

一个自组织映射训练的例证。蓝色斑点是训练数据的分布，而小白色斑点是从该分布中抽取得到的当前训练数据。首先（左图）SOM节点被任意地定位在数据空间中。我们选择最接近训练数据的节点作为获胜节点（用黄色突出显示）。它被移向训练数据，包括（在较小的范围内）其网格上的相邻节点。经过多次迭代后，网格趋于接近数据分布（右图）。