标签:电信号 保留 进制转换 src rom 文本 间接 取反 str
都知道计算机只认识0和1,只能支持二进制,那么计算机是如何记录现实世界中繁杂的语言符号呢?这就需要通过一系列的转换才可以了,下面我们就来认识一下二进制和编码。
进制也就是进位制,是人们规定的一种进位方法。 对于任何一种进制---X进制,就表示某一位置上的数运算时是逢X进一位。 十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,x进制就是逢x进位。二进制就是逢2进1,八进制就是逢8进1,以此类推;
对于整数常量,Java语言支持三种进制,八进制 十进制 十六进制;
任何数据在计算机中都是以二进制的形式存在的。二进制早期由电信号开关演变而来。一个整数在内存中一样也是二进制的,但是使用一大串的1或者0组成的数值进行使用很麻烦。所以就想把一大串缩短点,将二进制中的三位用一位表示。这三位可以取到的最大值就是7.超过7就进位了,这就是八进制。但是对于过长的二进制变成八进制还是较长,所以出现的用4个二进制位表示一位的情况,四个二进制位最大是15,这就是十六进制。规律,进制越大,表现形式越短。
十进制转换为二进制分为整数部分和小数部分
l 整数部分
方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个不走一直持续下去,知道商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。举例如下:
例:将十进制的168转换为二进制 将十进制的167转换为二进制
分析:第一步:将168除以2,商84,余数为0;将167除以2,商83,余数为1;
第二步:将84除以2,商42,余数为0;将83除以2,商41,余数为1;
第三步:将42除以2,商21,余数为0;将41除以2,商20,余数为1;
第四步:将21除以2,商10,余数为1;将20除以2,商10,余数为0;
第五步:将10除以2,商5,余数为0;将10除以2,商5,余数为0;
第六步:将5除以2,商2,余数为1;将5除以2,商2,余数为1;
第七步:将2除以2,商1,余数为0;将2除以2,商1,余数0;
第八步:将1除以2,商0,余数为1;将1除以2,商0,余数为1;
得出结果:将十进制的数168转换为二进制---(10101000)
将十进制的数167转换为二进制---(10100111)
l 小数部分
方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,以此类推直到小数部分为0为止.如果永远不能为0,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是0,舍掉,如果是1,向前入一位,换句话就是0舍1入。读数要从前面的整数读到后面的整数,举例说明。
例:将0.125换算为二进制
分析:第一步:将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;
第二步:将0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;
第三步:将0.5乘以2,得1.0,则整数部分为1,小数部分为0;
第四步:读数,从第一位读起,读到最后一位,即为0.001;
例:将0.45转换为二进制(保留到小数点第四位)
分析:第一步:将0.45乘以2,得0.9,则整数部分为0,小数部分为0.9;
第二步:将0.9乘以2,得1.8,则整数部分为1,小数部分为0.8;
第三步:将0.8乘以2,得1.6,则整数部分为1,小数部分为0.6;
第四步:将0.6乘以2,得1.2,则整数部分为1,小数部分为0.2;
第五步:将0.2乘以2,得0.4,则整数部分为0,小数部分为0.4;
从上面的步骤中可以看出,当第五次做乘法时,得到的结果是0.4,小数部分继续乘以2,是是永远不会使小数部分为0的,这个时候只好采取十进制的四舍五入了,但是在二进制中只有0和1,于是就出现了0舍1入。这个也是计算机在转换中产生误差,但是由于保留位数很多,精度很高所以忽略不计。那么,我们可以得出结果将0.45转换为二进制(保留到小数点后四位)等于0.0111。
从上面介绍的整数部分和小数部分我们可以注意到这么几点:
1.十进制转换为二进制时,需要分成整数部分和小数部分分别转换;
2.整数转换是除2,小数部分转换则是乘以2;
3.注意读数方向,整数部分是由下向上,小数部分是由上向下;
因此,我们从上面的方法可以得出十进制数转换为二进制数168.125=10101000.001
167.45(保留小数点后四位)=10100111.0111
l 二进制转换为十进制
二进制转换为十进制,不分小数部分和整数部分
方法:按权相加法,即将二进制每位上的数乘以权,然后相加之和既是十进制数,举例如下:
例:101.101转换为十进制数。
分析:第一步:整数部分1*2^2+0*2^1+1*2^0=5
第二步:小数部分1*2^-1+0*2^-2+1*2^-3=0.5+0+0.125=0.625
第三步:两者相加得5.625
在做二进制转换为十进制时需要注意:
1.要知道二进制的权值;整数部分从右往左一次我0,1,2....,小数部分从左往右依次为-1,-2...
2.要能求出每位的值;
首先我们需要知道这么几个东西二进制111转换为十进制为7,1000转换为十进制为8,所以我们可以知道八进制是由3位二进制来表示的;而十六进制是由4位二进制来表示的。
方法:取三合一法,即从二进制的小数点为分界点,向左(向右)每三位取成一位,接着将这三位二进制按权相加,得到的数就是一位八位二进制数,然后,按顺序进行排列,小数点的位置不变,得到的数字就是我们所求的八进制数。如果向左(向右)取三位后,取到最高(最低)位时候,如果无法凑足三位,可以在小数点最左边(最右边),即整数的最高位(最低位)添0,凑足三位。举列如下:
例1:将二进制数101110.101转换为八进制;
分析:第一步:我们将101110.101从右至左整数部分分为101 110,小数部分为101这三部分;
第二步:我们将分成的三部分(101 110 101)转换为八进制
1*2^2+0*2^1+1*2^0=5 1*2^2+1*2^1+0*2^0=6 1*2^2+0*2^1+1*2^0=5
第三步:将所得的数按照顺序组合得到56.5
例2:将二进制数1101.1转换为八进制
分析:第一步:我们将二进制数按三位分成一组,不够的话整数部分在最左边添加0,小数 部分在最右边添加0,分成的三组为001 101 100;
第二步:我们将分成的三组数转换为八进制001=1 101=5 100=4
第三步:将所得的数按照顺序组合得到15.4;
方法:取一分三法,即将一位八进制数分解成三位二进制数,用三位二进制按权相加去凑这位八进制数,小数点位置照旧。举例如下:
例1:将八进制数67.54转换为二进制
分析:第一步:我们将每一位八进制数转换为二进制:6<-->110 7<-->111 5<-->101 4<-->100
第二步:我们将所得数按照位置组合得到110111.101100,
第三步:因为这是八进制,在上面我们八进制转换为二进制时我们知道不够三位时的补 位方法所以我们可以将小数上面的0去掉,得数110111.1011;
以上就是二进制与八进制之间的相互转换,我们需要注意的是:
1.他们之间的转换是一位与三位转换,有别于二进制与十进制的转换;
2.我们在做需要填零时,要注意整数部分添加在最高位,小数部分添加在最低位;
方法:与二进制与八进制的转换相似,只不过是一位(十六进制)与四位(二进制)之间的转换;
方法:取四合一法,即从二进制的小数点为分界点,向左(向右)每四位取成一位,接着将这四位二进制按权相加,得到的数就是一位十六位二进制数,然后按顺序进行排列,小数点的位置不变,得到的数字就是我们所求的十六进制数。如果向左(向右)取四位后,取到最高(最低)位时候,如果无法凑足四位,可以在小数点最左边(最右边),即整数的最高位(最低位)添0,凑足四位。举例如下:
例1:将二进制数11101001.1011转换为十六进制
分析:第一步:以小数点为分界线将整数部分和小数部分按每四位分成一组得到三组数字
1110 1001 1011
第二步:将分得的二进制数转换为十六进制1110<-->1*2^3+1*2^2+1*2^1+0*2^0=14
1001<-->9 1011<-->11
第三步:将所得的数按顺序组合得到结果E9.B
例2:将二进制数101011.101转换为十六进制
分析:第一步:以小数点为分界线将整数部分和小数部分按每四位分成一组(整数部分不够 的在最高位(左边)上添0,小数部分不够在最低位(右边)上添0)得到三 组数字0010 1011 1010
第二步:将所得的二进制数转换为十六进制 0010<-->2 1011<-->11 1010<-->10
第三步:将所得的数按顺序组合得到结果2B.A
方法:取一分四法,即将一位十六进制数,即将一位十六进制数分解为四位二进制数,用四位二进制按权相加去凑这位十六进制数,小数点位置照旧。举例如下:
例1:将十六进制6E.2转换为二进制数
分析:第一步:将每一位十六进制数转换为二进制数 6<-->0110 E<-->1110 2<-->0010
第二步:按顺序组合得到最终结果为:1101110.001
方法:一般不能直接互相转换,一般将八进制(十六进制)先转换为二进制,然后再将二进制转换为十六进制(八进制),小数点位置不变。
方法:按权相加法,即将八进制每位上的数乘以位权,然后相加之和就是十进制数。举例如下:
例:将八进制数67.35转换为十进制数
分析:第一步:将八进制数分为整数部分和小数部分,将每部分上的每一位数乘以位权相加
6*8^1+7*8^0=55 3*8^-1+5*8^-2=0.453125
第二步:将所得结果按顺序排列得到最后结果:55.453
十进制转换为八进制有两种方式
l 间接法:先将十进制转换成二进制,然后将二进制转换成八进制
l 直接法:前面我们讲过八进制是由二进制衍生而来的,因此我们可以采取与十进制转换为二进制相似的办法,还是整数部分和小数部分两部分转换,下面具体讲解
整数部分
方法:除8取余法,即每次将整数部分除8,余数为该位权上的数,商继续除以8,余数为上一个位权上的数,依次往下直到商为0,最后读数时候从最后一个余数读起,到最前面一个余数为止;
小数部分
方法:乘8取整法,即小数部分乘以8取整数部分,剩下的小数部分继续乘以8,直到小数部分为0为止。若果永远不能为0,就同十进制数的四舍五入一样,暂取个名字叫3舍4入
例1:将十进制数796.703125转换为八进制数
分析:第一步:将十进制数以小数点为分界线分为整数部分和小数部分
第二步:将整数部分除8取余结果1434,小数部分乘8得到结果0.55
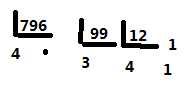
第三步:将结果汇总得到1434.55
十六进制与八进制有很多相似支出可以参照上面八进制与十进制的转换;
首先我们要知道这么一件事那就是整数属于int类型,而java中int类型是四个字节,那么他在计算机中就是以32位二进制形式存在的;我们以整数5来举例,5在计算机中的其实是是这样的00000000 000000000 00000000 00000101,那么-5是什么样的呢?在这里我们要知道这么几点:
例:5的原码: 00000000 00000000 00000000 00000101
-5的原码:10000000 00000000 00000000 00000101
例:5的反码: 00000000 00000000 00000000 00000101
-5的反码:11111111 11111111 11111111 11111010
例:5的补码:00000000 00000000 00000000 00000101
-5的补码:11111111 11111111 11111111 11111011
综上:我们可以对5与-5进行相加验证,超过32取消那么最后得到的就是:
00000000 00000000 000000000 00000000
计算机只认识0和1,甚至记录实际都是使用byte/bit等单位来记录的,那么文字该如何记录呢?事实上文本文件也是被记录成0和1的,这中间有一个转换的规则,那就是编码格式,我们按照某种编码规则,例如127代表“我”,那么汉字我在计算机中就是127来表示的,原理如下:
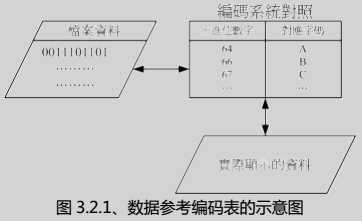
当我们需要读取文本文件时在经过解码,将127取出对照编码表返回一个“我”。目前最常用的编码规则是UTF-8.关于编码在这里不多做介绍了。
标签:电信号 保留 进制转换 src rom 文本 间接 取反 str
原文地址:http://www.cnblogs.com/lin-jing/p/7948285.html